排序算法可以分为:
- 内部排序:数据记录在内存中进行排序。
- 外部排序:因排序的数据很大,内存不能容纳全部的排序记录,在排序过程中需要访问外存。
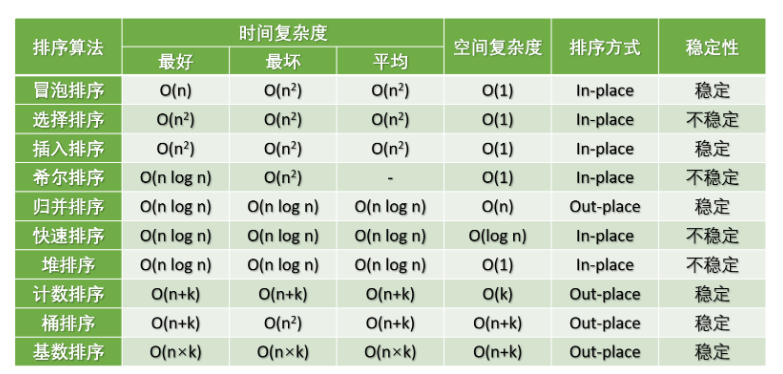
常见的内部排序算法有:插入排序、希尔排序、选择排序、冒泡排序、归并排序、快速排序、堆排序、基数排序、计数排序、桶排序。
其中比较类排序有:冒泡排序、快速排序、插入排序、希尔排序、选择排序、堆排序、归并排序
非比较类排序:计数排序、基数排序、桶排序
1、冒泡排序
算法步骤:从头或尾开始比较相邻的元素,如果逆序则交换,这样每遍历一次就会确定一个数的位置,重复以上步骤知道排序完成

1 public int[] bubbleSort(int[] arr){ 2 for(int i=1;i<arr.length;i++){ 3 boolean flag=true; 4 for(int j=0;j<arr.length-i;j++){ 5 if(arr[j]>arr[j+1]){ 6 int temp=arr[j]; 7 arr[j]=arr[j+1]; 8 arr[j+1]=temp; 9 flag=false; 10 } 11 } 12 if(flag)break; 13 } 14 return arr; 15 }
此处对代码做了一个小优化,加入了 is_sorted Flag,目的是将算法的最佳时间复杂度优化为 O(n),即当原输入序列就是排序好的情况下,该算法的时间复杂度就是 O(n)。
算法分析:
- 稳定性:稳定
- 时间复杂度:最佳:O(n) ,最差:O(n2), 平均:O(n2)
- 空间复杂度:O(1)
- 排序方式:交换排序
2、选择排序
算法步骤:从未排序的序列找到最小或者最大的放在指定位置,直到所有元素均有序

1 public static int[] selectionSort(int[] arr) { 2 for (int i = 0; i < arr.length - 1; i++) { 3 int minIndex = i; 4 for (int j = i + 1; j < arr.length; j++) { 5 if (arr[j] < arr[minIndex]) { 6 minIndex = j; 7 } 8 } 9 if (minIndex != i) { 10 int tmp = arr[i]; 11 arr[i] = arr[minIndex]; 12 arr[minIndex] = tmp; 13 } 14 } 15 return arr; 16 }
算法分析:
- 稳定性:不稳定
- 时间复杂度:最佳:O(n2) ,最差:O(n2), 平均:O(n2)
- 空间复杂度:O(1)
- 排序方式:选择排序
3、插入排序
步骤:对于未排序数据,在已排序序列中从后向前扫描,找到相应位置并插入。
public static int[] insertionSort(int[] arr) {
for (int i = 1; i < arr.length; i++) {
int preIndex = i - 1;
int current = arr[i];
while (preIndex >= 0 && current < arr[preIndex]) {
arr[preIndex + 1] = arr[preIndex];
preIndex -= 1;
}
arr[preIndex + 1] = current;
}
return arr;
}
- 稳定性:稳定
- 时间复杂度:最佳:O(n) ,最差:O(n2), 平均:O(n2)
- 空间复杂度:O(1)
- 排序方式:插入排序
4、希尔排序
算法步骤:先将整个待排序的记录序列分割成为若干子序列分别进行直接插入排序,待整个序列中的记录 “基本有序” 时,再对全体记录进行依次直接插入排序。
先将整个待排序的记录序列分割成为若干子序列分别进行直接插入排序,具体算法描述:
- 选择一个增量序列
{t1, t2, …, tk},其中(ti>tj, i<j, tk=1); - 按增量序列个数 k,对序列进行 k 趟排序;
- 每趟排序,根据对应的增量
t,将待排序列分割成若干长度为m的子序列,分别对各子表进行直接插入排序。仅增量因子为 1 时,整个序列作为一个表来处理,表长度即为整个序列的长度。
1 public static int[] shellSort(int[] arr) { 2 int n = arr.length; 3 int gap = n / 2; 4 while (gap > 0) { 5 for (int i = gap; i < n; i++) { 6 int current = arr[i]; 7 int preIndex = i - gap; 8 // Insertion sort 9 while (preIndex >= 0 && arr[preIndex] > current) { 10 arr[preIndex + gap] = arr[preIndex]; 11 preIndex -= gap; 12 } 13 arr[preIndex + gap] = current; 14 15 } 16 gap /= 2; 17 } 18 return arr; 19 }
算法分析:
- 稳定性:不稳定
- 时间复杂度:最佳:O(nlogn), 最差:O(n2) 平均:O(nlogn)
- 空间复杂度:
O(1)
5、归并排序
归并排序是一种稳定的排序方法。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。
归并排序算法是一个递归过程,边界条件为当输入序列仅有一个元素时,直接返回,具体过程如下:
- 如果输入内只有一个元素,则直接返回,否则将长度为
n的输入序列分成两个长度为n/2的子序列; - 分别对这两个子序列进行归并排序,使子序列变为有序状态;
- 设定两个指针,分别指向两个已经排序子序列的起始位置;
- 比较两个指针所指向的元素,选择相对小的元素放入到合并空间(用于存放排序结果),并移动指针到下一位置;
- 重复步骤 3 ~4 直到某一指针达到序列尾;
- 将另一序列剩下的所有元素直接复制到合并序列尾

1 public static int[] mergeSort(int[] arr) { 2 if (arr.length <= 1) { 3 return arr; 4 } 5 int middle = arr.length / 2; 6 int[] arr_1 = Arrays.copyOfRange(arr, 0, middle); 7 int[] arr_2 = Arrays.copyOfRange(arr, middle, arr.length); 8 return merge(mergeSort(arr_1), mergeSort(arr_2)); 9 } 10 11 /** 12 * Merge two sorted arrays 13 * 14 * @param arr_1 15 * @param arr_2 16 * @return sorted_arr 17 */ 18 public static int[] merge(int[] arr_1, int[] arr_2) { 19 int[] sorted_arr = new int[arr_1.length + arr_2.length]; 20 int idx = 0, idx_1 = 0, idx_2 = 0; 21 while (idx_1 < arr_1.length && idx_2 < arr_2.length) { 22 if (arr_1[idx_1] < arr_2[idx_2]) { 23 sorted_arr[idx] = arr_1[idx_1]; 24 idx_1 += 1; 25 } else { 26 sorted_arr[idx] = arr_2[idx_2]; 27 idx_2 += 1; 28 } 29 idx += 1; 30 } 31 if (idx_1 < arr_1.length) { 32 while (idx_1 < arr_1.length) { 33 sorted_arr[idx] = arr_1[idx_1]; 34 idx_1 += 1; 35 idx += 1; 36 } 37 } else { 38 while (idx_2 < arr_2.length) { 39 sorted_arr[idx] = arr_2[idx_2]; 40 idx_2 += 1; 41 idx += 1; 42 } 43 } 44 return sorted_arr; 45 }
算法分析:
- 稳定性:稳定
- 时间复杂度:最佳:O(nlogn), 最差:O(nlogn), 平均:O(nlogn)
- 空间复杂度:O(n)
6、快速排序
具体算法描述如下:
- 从序列中随机挑出一个元素,做为 “基准”(
pivot); - 重新排列序列,将所有比基准值小的元素摆放在基准前面,所有比基准值大的摆在基准的后面(相同的数可以到任一边)。在这个操作结束之后,该基准就处于数列的中间位置。这个称为分区(partition)操作;
- 递归地把小于基准值元素的子序列和大于基准值元素的子序列进行快速排序。

1 public static void quicksort(int[] arr, int left, int right) { 2 if (right >= left) { 3 //保存基数 4 int pivot = arr[left]; 5 //定义左右指针 6 int i = left; 7 int j = right; 8 while (i < j) { //左指针小于右指针 9 while (i < j && arr[j] > pivot) {//操作右指针找到小于基数的下标 10 j--; 11 } 12 if (i < j) { 13 arr[i] = arr[j]; //将右指针对应小于基数的值放到左指针所指的位置 14 i++; //左指针自加 15 } 16 while (i < j && arr[i] < pivot) {//相反,找到大于基数的下标 17 i++; 18 } 19 if (i < j) { 20 arr[j] = arr[i]; //大于基数的值赋给右指针所指的位置 21 j--; //右指针自减 22 } 23 } 24 arr[i] = pivot; //将基数放入到指针重合处 25 quicksort(arr, left, i - 1); //重复调用,对左半部分数组进行排序 26 quicksort(arr, i + 1, right); //对右半部分数组进行排序 27 } 28 }
算法分析:
- 稳定性:不稳定
- 时间复杂度:最佳:O(nlogn), 最差:O(nlogn),平均:O(nlogn)
- 空间复杂度:O(nlogn)
7、堆排序
堆是一个近似完全二叉树的结构,并同时满足堆的性质:即子结点的值总是小于(或者大于)它的父节点。
算法步骤:
- 将初始待排序列
(R1, R2, ……, Rn)构建成大顶堆,此堆为初始的无序区; - 将堆顶元素
R[1]与最后一个元素R[n]交换,此时得到新的无序区(R1, R2, ……, Rn-1)和新的有序区 (Rn), 且满足R[1, 2, ……, n-1]<=R[n]; - 由于交换后新的堆顶
R[1]可能违反堆的性质,因此需要对当前无序区(R1, R2, ……, Rn-1)调整为新堆,然后再次将 R [1] 与无序区最后一个元素交换,得到新的无序区(R1, R2, ……, Rn-2)和新的有序区(Rn-1, Rn)。不断重复此过程直到有序区的元素个数为n-1,则整个排序过程完成

1 private static void swap(int[] arr, int i, int j) { 2 int tmp = arr[i]; 3 arr[i] = arr[j]; 4 arr[j] = tmp; 5 } 6 private static void buildMaxHeap(int[] arr) { 7 for (int i = arr.length / 2 - 1; i >= 0; i--) { 8 heapify(arr, i); 9 } 10 } 11 12 private static void heapify(int[] arr, int i) { 13 int left = 2 * i + 1; 14 int right = 2 * i + 2; 15 int largest = i; 16 if (right < heapLen && arr[right] > arr[largest]) { 17 largest = right; 18 } 19 if (left < heapLen && arr[left] > arr[largest]) { 20 largest = left; 21 } 22 if (largest != i) { 23 swap(arr, largest, i); 24 heapify(arr, largest); 25 } 26 } 27 28 public static int[] heapSort(int[] arr) { 29 // index at the end of the heap 30 heapLen = arr.length; 31 // build MaxHeap 32 buildMaxHeap(arr); 33 for (int i = arr.length - 1; i > 0; i--) { 34 // Move the top of the heap to the tail of the heap in turn 35 swap(arr, 0, i); 36 heapLen -= 1; 37 heapify(arr, 0); 38 } 39 return arr; 40 }
算法分析:
- 稳定性:不稳定
- 时间复杂度:最佳:O(nlogn), 最差:O(nlogn), 平均:O(nlogn)
- 空间复杂度:O(1)
8、计数排序
计数排序使用一个额外的数组 C,其中第 i 个元素是待排序数组 A 中值等于 i 的元素的个数。然后根据数组 C 来将 A 中的元素排到正确的位置。它只能对整数进行排序。
- 找出数组中的最大值
max、最小值min; - 创建一个新数组
C,其长度是max-min+1,其元素默认值都为 0; - 遍历原数组
A中的元素A[i],以A[i]-min作为C数组的索引,以A[i]的值在A中元素出现次数作为C[A[i]-min]的值; - 对
C数组变形,新元素的值是该元素与前一个元素值的和,即当i>1时C[i] = C[i] + C[i-1]; - 创建结果数组
R,长度和原始数组一样。 - 从后向前遍历原始数组
A中的元素A[i],使用A[i]减去最小值min作为索引,在计数数组C中找到对应的值C[A[i]-min],C[A[i]-min]-1就是A[i]在结果数组R中的位置,做完上述这些操作,将count[A[i]-min]减小 1。

1 /** 2 * Gets the maximum and minimum values in the array 3 * 4 * @param arr 5 * @return 6 */ 7 private static int[] getMinAndMax(int[] arr) { 8 int maxValue = arr[0]; 9 int minValue = arr[0]; 10 for (int i = 0; i < arr.length; i++) { 11 if (arr[i] > maxValue) { 12 maxValue = arr[i]; 13 } else if (arr[i] < minValue) { 14 minValue = arr[i]; 15 } 16 } 17 return new int[] { minValue, maxValue }; 18 } 19 20 /** 21 * Counting Sort 22 * 23 * @param arr 24 * @return 25 */ 26 public static int[] countingSort(int[] arr) { 27 if (arr.length < 2) { 28 return arr; 29 } 30 int[] extremum = getMinAndMax(arr); 31 int minValue = extremum[0]; 32 int maxValue = extremum[1]; 33 int[] countArr = new int[maxValue - minValue + 1]; 34 int[] result = new int[arr.length]; 35 36 for (int i = 0; i < arr.length; i++) { 37 countArr[arr[i] - minValue] += 1; 38 } 39 for (int i = 1; i < countArr.length; i++) { 40 countArr[i] += countArr[i - 1]; 41 } 42 for (int i = arr.length - 1; i >= 0; i--) { 43 int idx = countArr[arr[i] - minValue] - 1; 44 result[idx] = arr[i]; 45 countArr[arr[i] - minValue] -= 1; 46 } 47 return result; 48 }
算法分析:
当输入的元素是 n 个 0 到 k 之间的整数时,它的运行时间是 O(n+k)。计数排序不是比较排序,排序的速度快于任何比较排序算法。由于用来计数的数组 C 的长度取决于待排序数组中数据的范围(等于待排序数组的最大值与最小值的差加上 1),这使得计数排序对于数据范围很大的数组,需要大量额外内存空间。
- 稳定性:稳定
- 时间复杂度:最佳:
O(n+k)最差:O(n+k)平均:O(n+k) - 空间复杂度:
O(k)
- 设置一个 BucketSize,作为每个桶所能放置多少个不同数值;
- 遍历输入数据,并且把数据依次映射到对应的桶里去;
- 对每个非空的桶进行排序,可以使用其它排序方法,也可以递归使用桶排序;
- 从非空桶里把排好序的数据拼接起来

1 private static int[] getMinAndMax(List<Integer> arr) { 2 int maxValue = arr.get(0); 3 int minValue = arr.get(0); 4 for (int i : arr) { 5 if (i > maxValue) { 6 maxValue = i; 7 } else if (i < minValue) { 8 minValue = i; 9 } 10 } 11 return new int[] { minValue, maxValue }; 12 } 13 14 15 public static List<Integer> bucketSort(List<Integer> arr, int bucket_size) { 16 if (arr.size() < 2 || bucket_size == 0) { 17 return arr; 18 } 19 int[] extremum = getMinAndMax(arr); 20 int minValue = extremum[0]; 21 int maxValue = extremum[1]; 22 int bucket_cnt = (maxValue - minValue) / bucket_size + 1; 23 List<List<Integer>> buckets = new ArrayList<>(); 24 for (int i = 0; i < bucket_cnt; i++) { 25 buckets.add(new ArrayList<Integer>()); 26 } 27 for (int element : arr) { 28 int idx = (element - minValue) / bucket_size; 29 buckets.get(idx).add(element); 30 } 31 for (int i = 0; i < buckets.size(); i++) { 32 if (buckets.get(i).size() > 1) { 33 buckets.set(i, sort(buckets.get(i), bucket_size / 2)); 34 } 35 } 36 ArrayList<Integer> result = new ArrayList<>(); 37 for (List<Integer> bucket : buckets) { 38 for (int element : bucket) { 39 result.add(element); 40 } 41 } 42 return result; 43 }
算法分析:
- 稳定性:稳定
- 时间复杂度:最佳:
O(n+k)最差:O(n²)平均:O(n+k) - 空间复杂度:
O(k)
10、基数排序
基数排序是按照低位先排序,然后收集;再按照高位排序,然后再收集;依次类推,直到最高位。

1 public static int[] radixSort(int[] arr) { 2 if (arr.length < 2) { 3 return arr; 4 } 5 int N = 1; 6 int maxValue = arr[0]; 7 for (int element : arr) { 8 if (element > maxValue) { 9 maxValue = element; 10 } 11 } 12 while (maxValue / 10 != 0) { 13 maxValue = maxValue / 10; 14 N += 1; 15 } 16 for (int i = 0; i < N; i++) { 17 List<List<Integer>> radix = new ArrayList<>(); 18 for (int k = 0; k < 10; k++) { 19 radix.add(new ArrayList<Integer>()); 20 } 21 for (int element : arr) { 22 int idx = (element / (int) Math.pow(10, i)) % 10; 23 radix.get(idx).add(element); 24 } 25 int idx = 0; 26 for (List<Integer> l : radix) { 27 for (int n : l) { 28 arr[idx++] = n; 29 } 30 } 31 } 32 return arr; 33 }
算法分析:
- 稳定性:稳定
- 时间复杂度:最佳:
O(n×k)最差:O(n×k)平均:O(n×k) - 空间复杂度:
O(n+k)




