树状数组『蒟蒻笔记』
笔者蒟蒻一只,如有错误和不准确不严谨的地方望指正 orz
什么是树状数组
树状数组 \(=\) 二进制索引数 \(=\) BIT ( Binary Indexed Tree
可以用来求序列的前缀和,将复杂度降到 \(O(log_{10}n)\)
大致图为(以前16个数为例
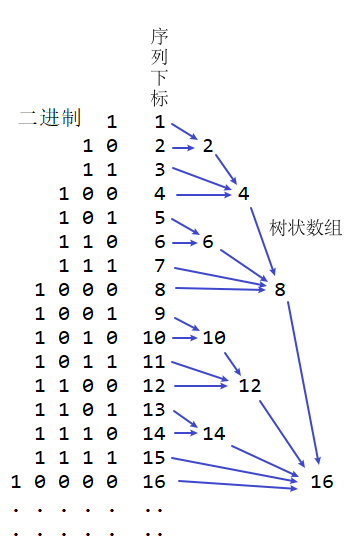
图中的非叶子节点都代表这一个区间的和如点 \(2\) 代表原序列中\(1\) 到 \(2\) 的和,点 \(12\) 代表原序列中 \(9\) 到 \(12\) 的和,叶子节点就代表它自己如点 \(5\) 就等于原序列中第五个数,我们把树上的节点用数组 \(t\) 来表示。
至此我们观察出若求原序列中前 \(15\) 个数的和则只需要求出树上 \(t[15]\) \(t[14]\) \(t[12]\) \(t[8]\) ,并对它们求和即可,使求和变得十分高效
树状数组的实现方法 \(\to\) lowbit()
int lowbit(int x){return x&-x;}
头次看到这简短的一行代码作为蒟蒻的我是满脸问号的 (\(\tt{? ?????????????}\)
先说\(lowbit\)的用处吧:一个参数,传入的是当前节点编号,返回一个整型,距相邻节点的距离也是当前节点所能管辖的距离,举例:如上图中的节点 \(6\) ,\(lowbit(6)=2\),所以我们知道节点 \(6\) 的上一个节点是 \(4\) 因为 \(6-2=4\) 同理下一个节点是 \(8\quad(6+2=8)\) 。再比如说节点 \(8\) , \(lowbit(8)=8\) 所以节点 \(8\) 的上一个节点因为 \(8-8=0\quad 0<1\) 所以不存在,下一个节点为 \(16\quad (8+8=16)\) (这里的上一个节点和下一个节点指的是前缀和管辖的区间节点, \(lowbit\) 返回的也是管辖的距离,管辖是指求一段区间的和
这是怎么做到的呢?
我们观察函数内部 发现了 \(x\) 和 \(-x\) 两个数, \(x\) 我们都知道,是传进来的节点编号,而 \(-x\) 是传进来节点编号的相反数,为什么要找相反数呢,我们接着看,\(x\) 和 \(-x\) 之间用 \(\&\) 符号相连表示对两个数进行 与运算 这又可以得到什么呢?
再来几个例子吧 继续用节点 \(6\) , \(6\) 的二进制表示为 \((110)\) 而 \(-6\) 的二进制表示为对 \(6\) 而二进制表示取反并加一 :\((001)+(001)=(010)\) ,\((010)\)!,这不就是 \(2\) 的二进制表示嘛,就这样我们得到了 \(6\) 的管辖区域长度也是距离上下节点的距离: \(2\) ,而 \(lowbit\) 的 \(x\&-x\) 这套花里胡哨操作其实就是在找 \(x\) 二进制中第一个不为 \(0\) 的位置,剩下的位置补零转化为十进制后输出就成了神奇的我们要找的值
这是我们再来看求前缀和是不是就有思路了 求前十五个数的操作步骤:
- 初始化 \(x=15\)
- \(sum+=t[x],x=x-lowbit[x]\)
- \(sum+=t[x],x=x-lowbit[x]\)
- . . .
- 如此循环至 \(x<1\) 结束
这样 sum[15] 就求出来了
再来看单点修改的操作,知道了求和的过程其实修改就是求和的逆过程,对点 \(3\) 进行 \(+c\) 操作步骤:
- 初始化 \(x=3\)
- \(t[x]+=c,x=x+lowbit(x)\)
- \(t[x]+=c,x=x+lowbit(x)\)
- . . . .
- 如此循环至 \(x>n\) ( \(n\) 为序列长度
理解之后本蒟蒻大呼妙啊
例题:P1908 逆序对
洛谷P1908 \(\to\) Click Here
这道题看起来跟前缀和没什么关系,但确实是本蒟蒻入门树状数组的第一道题
题意
求一个序列中逆序对的个数
思路
我们把原数列 \(a\) 离散化,用 \(d[i]\) 来表示原序列中第 \(i\) 大的数所在的位置(下标,再将 \(d\) 从 \(1\) 到 \(n\) 地插入到树状数组中,在插入之后求一下在 \(d[i]\) 之前的数有多少个,即比 \(a[i]\) 还大但插入到了 \(a[i]\) 之前的数有几个
求在 \(d[i]\) 之前的数的数量就用到了今天学到的树状数组了
code
//求 $d$ :
for(int i=1,i<=n,i++){
a[i]=read();
d[i]=i;
}
sort(d+1,d+n+1,cmp1);离散化求d[i]
//插入(Add() :
void Add(int x){
while(x<=n){
t[x]++;
x+=lowbit(x);
}
}
//查找(Query() :
int Query(int x){
int res=0;
while(x>=1){
res+=t[x];
x-=lowbit(x);
}
return res;
}
//完整code:
#include<iostream>
#include<algorithm>
#define int long long//记得开long long
#define REP(i,a,b) for(int i=(a);i<=(b);i++)
#define FOR(i,a,b) for(int i=(a);i<(b);i++)
using namespace std;
const int N = 500005;
int n,ans;
int a[N],d[N],t[N];
int read(){//需要较快的读入
int x=0,f=1;
char ch=getchar();
while(ch<'0'||ch>'9'){
if(ch=='-') f=-1;
ch=getchar();
}
while(ch>='0'&&ch<='9'){
x=(x<<1)+(x<<3)+(ch^48);
ch=getchar();
}
return x*f;
}
bool cmp1(int x,int y){
if(a[x]==a[y]) return x>y;
return a[x]>a[y];
}
int lowbit(int x){return x&-x;}
void Add(int x){
while(x<=n){
t[x]++;
x+=lowbit(x);
}
}
int Query(int x){
int res=0;
while(x>=1){
res+=t[x];
x-=lowbit(x);
}
return res;
}
void solve(){
n=read();
REP(i,1,n){
a[i]=read();
d[i]=i;
}
sort(d+1,d+n+1,cmp1);//离散化求d[i]
for(int i=1;i<=n;i++){
Add(d[i]);//在树状数组中添加一个数
ans+=Query(d[i]-1);//求在这个数的位置之前已经添加了多少比它大的数
}
cout<<ans<<endl;
}
signed main(){
solve();
return 0;
}





 浙公网安备 33010602011771号
浙公网安备 33010602011771号