优化

书接上回，那个数列求和，我感觉有优化的空间，后面想了想，确实可以优化到O(1),所以想分享一下我的思维过程。

1. 题目：输入n和a，求s = a + aa + aaa + aaaa + aa...a的值，其中n、a是数字。例如n=5，a=2时，求2 + 22 + 222 + 2222 + 22222的值。

之前想算出一共有多少个a，假设有Sn个a,结果就是Sn * a，因此我只需要算出一共有多少个a即可。
观察s的结构，可以知道他是一个三角形,如下：
    a
   aa
  aaa
 aaaa
aaaaa
一共有多少个a？**表达式**为 n+(n-1)*10+(n-2)*10^2+(n-3)*10^3...

2.因此我只需要求出这个表达式（n + (n-1) * 10 + (n-2) * 10^2 + (n-3) * 10^3...）即可

不严谨证明如下:
首先我将表达式拆开：
我先看前两项：n + 10n -10
再看前三项：n + 10n + 100n - 210
再看第四项: n + 10n + 100n + 1000n - 3210
设该表达式的通项为cn，很明显，cn = an - bn
an等于n *（10^n - 1） / 9
因此要求cn，则只需要将bn求出即可

3.如何求出一个数列规律为（0 10 210 3210 43210 ...)的一个数列

可以将该问题转换为如下的一个数列问题：
已知 bn = bn-1 + (n - 1) * 10 ^ (n - 1),且b1 = 0,求bn 

4. 使用deepseek求得 bn = ((9n - 10) *10 ^ n + 10) / 81

5. 因此cn = n * (10 ^ n -1) / 9 - ((9n - 10) * 10 ^ n + 10) / 81

化简一下cn，cn = (10 ^ (n + 1) - 9n - 10) / 81
最终优化代码为
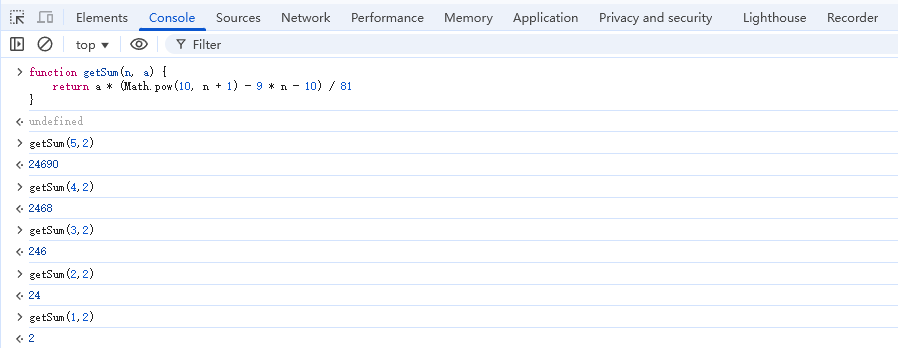
function getSum(n: number, a: number): number {
    return a * (Math.pow(10, n + 1) - 9 * n - 10) / 81
}