算法之动态规划学习
动态规划的核⼼思想就是穷举求最值,但是问题可以千变万化,穷举所有可⾏解其实并不是⼀件容易的事,只有列出正确的「状态转移⽅程」才能正确地穷举。
动态规划三要素:重叠⼦问题、最优⼦结构、状态转移⽅程。
状态转移⽅程思路:
状态转移⽅程思路:
明确「状态」 -> 定义 dp 数组/函数的含义 -> 明确「选择」-> 明确 base case。
下⾯通过斐波那契数列问题和凑零钱问题来详解动态规划的基本原理。
前者主要是让你明⽩什么是重叠⼦问题(斐波那契数列严格来说不是动态规划问题),
后者主要举集中于如何列出状态转移⽅程。
⼀、斐波那契数列
1、暴⼒递归
斐波那契数列指的是这样一个数列 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233,377,610,987,1597,2584,4181,6765,10946,17711,28657,46368……
特别指出:第0项是0,第1项是第一个1。 一般考题就是想要计算第N个数据的值是多少?
这个数列从第三项开始,每一项都等于前两项之和。
以下实例演示了 Java 斐波那契数列的实现:
public class MainClass { public static void main(String[] args) { for (int counter = 0; counter <= 10; counter++){ System.out.printf("Fibonacci of %d is: %d\n", counter, fibonacci(counter)); } } public static long fibonacci(long number) { if ((number == 0) || (number == 1)) return number; else return fibonacci(number - 1) + fibonacci(number - 2); } }
以上代码运行输出结果为:
Fibonacci of 0 is: 0 Fibonacci of 1 is: 1 Fibonacci of 2 is: 1 Fibonacci of 3 is: 2 Fibonacci of 4 is: 3 Fibonacci of 5 is: 5 Fibonacci of 6 is: 8 Fibonacci of 7 is: 13 Fibonacci of 8 is: 21 Fibonacci of 9 is: 34 Fibonacci of 10 is: 55
核心代码就是:
int fib(int N) { if (N == 1 || N == 2) return 1; return fib(N - 1) + fib(N - 2); }
PS:但凡遇到需要递归的问题,最好都画出递归树,这对你分析算法的复杂度,寻找算法低效的原因都有巨⼤帮助。
假设 n = 20,请画出递归树 想要计算第N个数是多少?
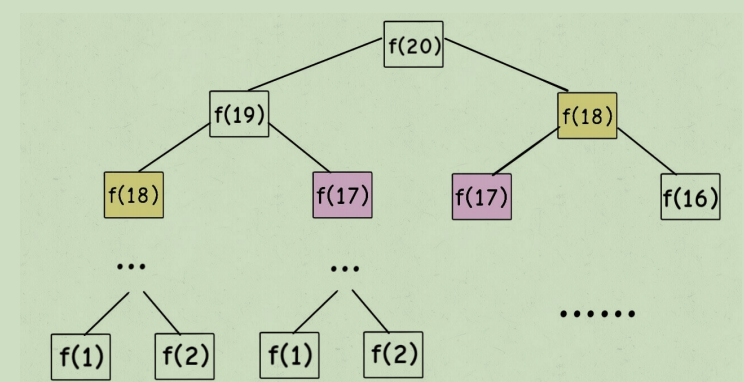
理解过程如下:
想要计算原问题 f(20) ,我就得先计算出⼦问题 f(19) 和 f(18) ,然后要计算 f(19) ,我就要先算出⼦问题 f(18)和 f(17) ,以此类推。最后遇到 f(1) 或者 f(2) 的时候,结果已知,就
能直接返回结果,递归树不再向下⽣⻓了。
想要计算问题f(N),就得知道f(N-1) 和 f(N-2),依次类推。
递归算法的时间复杂度怎么计算?⼦问题个数乘以解决⼀个⼦问题需要的时间。
⼦问题个数,即递归树中节点的总数。显然⼆叉树节点总数为指数级别,所以⼦问题个数为 O(2^n)。
解决⼀个⼦问题的时间,在本算法中,没有循环,只有 f(n - 1) + f(n - 2) ⼀个加法操作,时间为 O(1)。
==========================================================================================
所以,这个算法的时间复杂度为 O(2^n),指数级别,爆炸。观察递归树,很明显发现了算法低效的原因:存在⼤量重复计算,⽐如f(18) 被计算了两次,⽽且你可以看到,以 f(18) 为根的这个递归树体量巨⼤,多算⼀遍,会耗费巨⼤的时间。更何况,还不⽌ f(18) 这⼀个节点被重复计算,所以这个算法及其低效。
这就是动态规划问题的第⼀个性质:重叠⼦问题。下⾯,我们想办法解决这个问题。
时间复杂度问题,我已在:https://www.cnblogs.com/controller666/articles/12153095.html 总结过了。
2、带备忘录的递归解法(备份已算过的节点(子问题))
即然耗时的原因是重复计算,那么我们可以造⼀个「备忘录」,每次算出某个⼦问题的答案后别急着返回,先记到「备忘录」⾥再返回;每次遇到⼀个⼦问题先去「备忘录」⾥查
⼀查,如果发现之前已经解决过这个问题了,直接把答案拿出来⽤,不要再耗时去计算了。⼀般使⽤⼀个数组充当这个「备忘录」,当然你也可以使⽤哈希表(字典),思想都是⼀样的。
int fib(int N) {
if (N < 1) return 0;
// 备忘录全初始化为0
int [] memo = new int[N+1];
for(int i= 0;i<=N;i++){
memo[i] = 0;
}
// 初始化最简情况
return helper(memo, N);
}
int helper(int [] memo, int n) {
// base case
if (n == 1 || n == 2)
return 1;
// 已经计算过
if (memo[n] != 0) return memo[n];
memo[n] = helper(memo, n - 1) + helper(memo, n - 2);
return memo[n];
}
//另一种写法
public int res[];
public int Fibonacci1(int n) {
res = new int[n + 1];
for (int i = 0; i < n + 1; i++){ res[i] = -1;
}
return fun(n);
public int fun(int n) {
if (n == 0) {
res[n] = 0;
return 0;
}if (n == 1) { res[n] = 1; return 1; } if (res[n] != -1) return res[n]; res[n] = fun(n - 1) + fun(n - 2); return res[n];}
画出改造后的递归树:
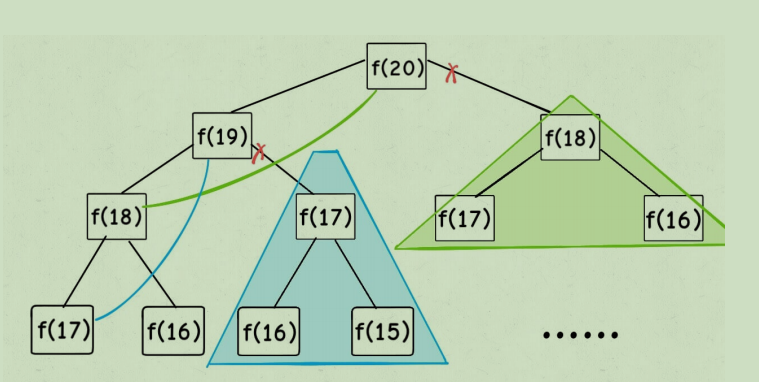
实际上,带「备忘录」的递归算法,把⼀棵存在巨量冗余的递归树通过「剪枝」,改造成了⼀幅不存在冗余的递归图,极⼤减少了⼦问题(即递归图中节点)的个数。
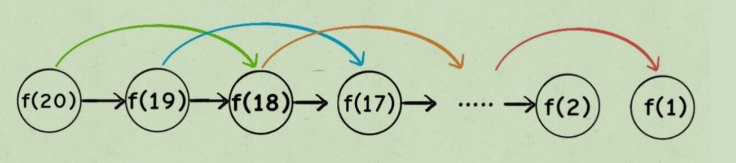
那这个带备忘录递归算法的时间复杂度怎么算?⼦问题个数乘以解决⼀个⼦问题需要的时间。
⼦问题个数,即图中节点的总数,由于本算法不存在冗余计算,⼦问题就是f(1) , f(2) , f(3) ... f(20) ,数量和输⼊规模 n = 20 成正⽐,所以⼦问题个数为 O(n)。
解决⼀个⼦问题的时间,同上,没有什么循环,时间为 O(1)。
所以,本算法的时间复杂度是 O(n)。⽐起暴⼒算法,是降维打击。
⾄此,带备忘录的递归解法的效率已经和迭代的动态规划解法⼀样了。实际上,这种解法和迭代的动态规划已经差不多了,只不过这种⽅法叫做「⾃顶向下」,动态规划叫做「⾃底向上」。
3、dp 数组的迭代解法
有了上⼀步「备忘录」的启发,我们可以把这个「备忘录」独⽴出来成为⼀张表,就叫做 DP table 。
这道题也可以作为动态规划入门题,动态规划实际是一个填表的过程,要求解
f(n)则必须知道子问题,因此先解决最小的子问题,即从0,1,2…开始int Fibonacci2(int N){ int[] dp = new int[N + 1]; dp[0] = 0; dp[1] = dp[2] = 1; for(int i = 3;i <=N;i++){ dp[i] = dp[i-1] + dp[i-2]; } return dp[N]; }
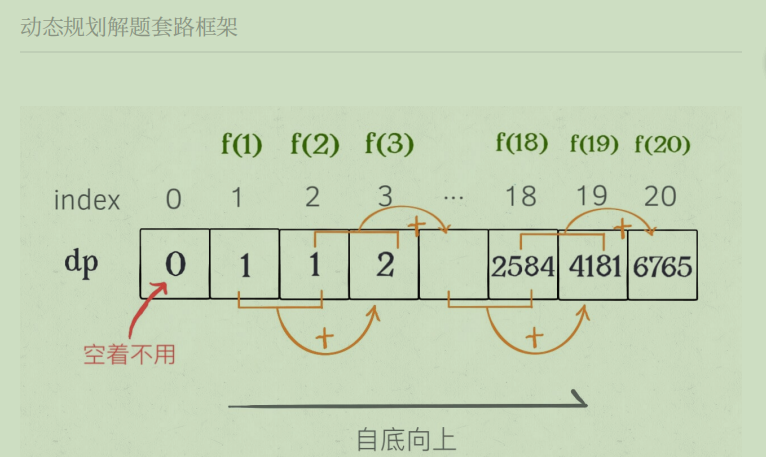
画个图就很好理解了,⽽且你发现这个 DP table 特别像之前那个「剪枝」后的结果,只是反过来算⽽已。实际上,带备忘录的递归解法中的「备忘录」,最终完成后就是这个 DP table,所以说这两种解法其实是差不多的,⼤部分情况下,效率也基本相同。
这⾥,引出「状态转移⽅程」这个名词,实际上就是描述问题结构的数学公式:
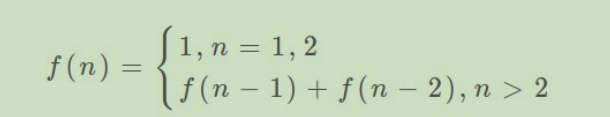
为啥叫「状态转移⽅程」?为了听起来⾼端。你把 f(n) 想做⼀个状态 n,这个状态 n 是由状态 n - 1 和状态 n - 2 相加转移⽽来,这就叫状态转移,仅此⽽已。
其实状态转移⽅程直接代表着暴⼒解法。
千万不要看不起暴⼒解,动态规划问题最困难的就是写出状态转移⽅程,即这个暴⼒解。优化⽅法⽆⾮是⽤备忘录或者 DP table。
这个例⼦的最后,讲⼀个细节优化。细⼼的读者会发现,根据斐波那契数列的状态转移⽅程,当前状态只和之前的两个状态有关,其实并不需要那么⻓的⼀个 DP table 来存储所有的状态,只要想办法存储之前的两个状态就⾏了。所以,可以进⼀步优化,把空间复杂度降为 O(1):
int Fibonacci3(int n) { if (n == 2 || n == 1) return 1; //定义前一个,和现在的变量(状态) // 算出前一个加现在 即为后一个, // 替换原来现在为前一个,后一个为现在,再求新的值 依次类推 返回现在的值 int prev = 1, curr = 1; for (int i = 3; i <= n; i++) { int sum = prev + curr; prev = curr; curr = sum; } return curr; }
============================================================================================
下面讲
动态规划的另⼀个重要特性「最优⼦结构」
⼆、凑零钱问题(最值问题)
先看下题⽬:给你 k 种⾯值的硬币,⾯值分别为 c1, c2 ... ck ,每种硬币的数量⽆限,再给⼀个总⾦额 amount ,问你最少需要⼏枚硬币凑出这个⾦额,如果不可能凑出,算法返回 -1 。算法的函数签名如下:
// coins 中是可选硬币⾯值,amount 是⽬标⾦额 int coinChange(int[] coins, int amount);
⽐如说 k = 3 ,⾯值分别为 1,2,5,总⾦额 amount = 11 。那么最少需要 3 枚硬币凑出,即 11 = 5 + 5 + 1。
你认为计算机应该如何解决这个问题?显然,就是把所有肯能的凑硬币⽅法都穷举出来,然后找找看最少需要多少枚硬币。
===========================================================================================
1、暴⼒递归
⾸先,这个问题是动态规划问题,因为它具有「最优⼦结构」的。要符合【最优⼦结构】,⼦问题间必须互相独⽴。啥叫相互独⽴?
⽐如说,你的原问题是考出最⾼的总成绩,那么你的⼦问题就是要把语⽂考到最⾼,数学考到最⾼…… 为了每门课考到最⾼,你要把每门课相应的选择题分数拿到最⾼,填空题分数拿到最⾼…… 当然,最终就是你每门课都是满分,这就是最⾼的总成绩。
得到了正确的结果:最⾼的总成绩就是总分。因为这个过程符合最优⼦结构,“每门科⽬考到最⾼”这些⼦问题是互相独⽴,互不⼲扰的。
但是,如果加⼀个条件:你的语⽂成绩和数学成绩会互相制约,此消彼⻓。这样的话,显然你能考到的最⾼总成绩就达不到总分了,按刚才那个思路就会得到错误的结果。因为⼦问题并不独⽴,语⽂数学成绩⽆法同时最优,所以最优⼦结构被破坏。
回到凑零钱问题,为什么说它符合最优⼦结构呢?⽐如你想求 amount =11 时的最少硬币数(原问题),如果你知道凑出 amount = 10 的最少硬币数(⼦问题),你只需要把⼦问题的答案加⼀(再选⼀枚⾯值为 1 的硬币)就是原问题的答案,因为硬币的数量是没有限制的,⼦问题之间没有相互制,是互相独⽴的。
那么,既然知道了这是个动态规划问题,就要思考如何列出正确的状态转移⽅程?
先确定「状态」,也就是原问题和⼦问题中变化的变量。由于硬币数量⽆限,所以唯⼀的状态就是⽬标⾦额 amount 。
然后确定 dp 函数的定义:当前的⽬标⾦额是 n ,⾄少需要 dp(n) 个硬币凑出该⾦额。
然后确定「选择」并择优,也就是对于每个状态,可以做出什么选择改变当前状态。具体到这个问题,⽆论当的⽬标⾦额是多少,选择就是从⾯额列表coins 中选择⼀个硬币,然后⽬标⾦额就会减少:
下面是伪代码:
# 伪码框架 def coinChange(coins: List[int], amount: int): # 定义:要凑出⾦额 n,⾄少要 dp(n) 个硬币 def dp(n): # 做选择,选择需要硬币最少的那个结果 for coin in coins: res = min(res, 1 + dp(n - coin)) return res # 我们要求的问题是 dp(amount)
return dp(amount)
最后明确 base case,显然⽬标⾦额为 0 时,所需硬币数量为 0;当⽬标⾦额⼩于 0 时,⽆解,返回 -1:
def coinChange(coins: List[int], amount: int): def dp(n): # base case if n == 0: return 0 if n < 0: return -1 # 求最⼩值,所以初始化为正⽆穷 res = float('INF') for coin in coins: subproblem = dp(n - coin) # ⼦问题⽆解,跳过 if subproblem == -1: continue res = min(res, 1 + subproblem) return res if res != float('INF') else -1 return dp(amount)
不忘初心,相信自己,坚持下去,付诸实施。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号