数据结构与算法学习（二）--复杂度分析

优秀博文：

https://blog.csdn.net/ws9029/article/details/109398268 

https://blog.csdn.net/qq_36582604/article/details/81661236

 

一、复杂度分析的4个概念
1.最坏情况时间复杂度：代码在最理想情况下执行的时间复杂度。
2.最好情况时间复杂度：代码在最坏情况下执行的时间复杂度。
3.平均时间复杂度：用代码在所有情况下执行的次数的加权平均值表示。
4.均摊时间复杂度：在代码执行的所有复杂度情况中绝大部分是低级别的复杂度，个别情况是高级别复杂度且发生具有时序关系时，可以将个别高级别复杂度均摊到低级别复杂度上。基本上均摊结果就等于低级别复杂度。

二、为什么要引入这4个概念？
1.同一段代码在不同情况下时间复杂度会出现量级差异，为了更全面，更准确的描述代码的时间复杂度，所以引入这4个概念。
2.代码复杂度在不同情况下出现量级差别时才需要区别这四种复杂度。大多数情况下，是不需要区别分析它们的。

三、如何分析平均、均摊时间复杂度？
1.平均时间复杂度
代码在不同情况下复杂度出现量级差别，则用代码所有可能情况下执行次数的加权平均值表示。
2.均摊时间复杂度
两个条件满足时使用：1）代码在绝大多数情况下是低级别复杂度，只有极少数情况是高级别复杂度；2）低级别和高级别复杂度出现具有时序规律。均摊结果一般都等于低级别复杂度。

 

个人体会: 平均和平摊基本就是一个概念，平摊是特殊的平均。在分析时间复杂度是O(1)还是O(n)的时候最简单就是凭感觉，，，，，，，，出现O(1)的次数远大于出现O(n)出现的次数，那么平均平摊时间复杂度就是O(1)。。。。

举例1：

// 全局变量，大小为10的数组array，长度len，下标i。
int array[] = new int[10]; 
int len = 10;//len为此方法中的不确定数值，就是变量，影响时间复杂度的数据。
int i = 0;

// 往数组中添加一个元素
void add(int element) {
   if (i >= len) { // 数组空间不够了
     // 重新申请一个2倍大小的数组空间
     int new_array[] = new int[len*2];
     // 把原来array数组中的数据依次copy到new_array
     for (int j = 0; j < len; ++j) {
       new_array[j] = array[j];
     }
     // new_array复制给array，array现在大小就是2倍len了
     array = new_array;
     len = 2 * len;
   }
   // 将element放到下标为i的位置，下标i加一
   array[i] = element;
   ++i;
}

分析时间复杂度：

方法1、

1. 最好情况时间复杂度为 O(1)
2.最坏情况分析：
最坏情况代码执行的次数跟每次数组的长度有关---最坏的情况就是数组不够了，最坏情况时间复杂度为O(n);
第1次调用insert的执行的次数为 n ,
第2次调用insert的执行的次数为 2n ,
第3次调用insert的执行的次数为 2^2 * n
第k次调用insert的执行的次数为 2^(k-1) * n
最坏时间复杂度为 O(n)。
3. 平均情况分析
当每次遇到最坏情况时数组会进行2倍扩容，原数组被导入新数组，虽然数组的长度变大了，但是插入操作落在的区间的长度是一样的，分别是0~len-1, len~(2len-1),....；
插入的情况仍是len+1种：0~len-1和插满之后的O(len)；所以每次插入的概率是：p= 1/len+1，
最后求出加权平均时间复杂度为 1*p + 2*p+ ▪▪▪ + len*p + len * p = O(1) ;
4. 均摊时间复杂度 O(1)
而均摊复杂度由于每次O(len)的出现都跟着len次O(1)，是前后连贯的，因而将O(len)平摊到前len次上，得出平摊复杂度是O(1)。

分析方法2：

1、最好情况时间复杂度：
当i<len时，直接往数组中添加一个元素，时间复杂度是O(1)。
2、最坏情况时间复杂度：
当i>=len时，数组空间不够，走了for循环，时间复杂度是O(n)。
3、平均情况时间复杂度：
有n+1种情况，而且，这 n+1 种情况发生的概率一样，都是 1/(n+1)。
(1+1+...+1+n)/(n+1) = 2n/(n+1)，所以时间复杂度为O(1)。

举例2：

 // array表示一个长度为n的数组
 // 代码中的array.length就等于n
 int[] array = new int[n];
 int count = 0;
 
 void insert(int val) {
    if (count == array.length) {
       int sum = 0;
       for (int i = 0; i < array.length; ++i) {
          sum = sum + array[i];
       }
       array[0] = sum;
       //count被重置为1。之后再插入的数据就会覆盖掉原来的数据。就相当于将原数组清空了。并不需要显示的去清空
       count = 1;
    }

    array[count] = val;
    ++count;
 }

 

我先来解释一下这段代码。这段代码实现了一个往数组中插入数据的功能。当数组满了之后，也就是代码中的 count == array.length 时，我们用 for 循环遍历数组求和，并清空数组，将求和之后的 sum 值放到数组的第一个位置，然后再将新的数据插入。但如果数组一开始就有空闲空间，则直接将数据插入数组。那这段代码的时间复杂度是多少呢？你可以先用我们刚讲到的三种时间复杂度的分析方法来分析一下。最理想的情况下，数组中有空闲空间，我们只需要将数据插入到数组下标为 count 的位置就可以了，所以最好情况时间复杂度为 O(1)。最坏的情况下，数组中没有空闲空间了，我们需要先做一次数组的遍历求和，然后再将数据插入，所以最坏情况时间复杂度为 O(n)。那平均时间复杂度是多少呢？答案是 O(1)。我们还是可以通过前面讲的概率论的方法来分析。假设数组的长度是 n，根据数据插入的位置的不同，我们可以分为 n 种情况，每种情况的时间复杂度是 O(1)。除此之外，还有一种“额外”的情况，就是在数组没有空闲空间时插入一个数据，这个时候的时间复杂度是 O(n)。而且，这 n+1 种情况发生的概率一样，都是 1/(n+1)。所以，根据加权平均的计算方法，我们求得的平均时间复杂度就是：

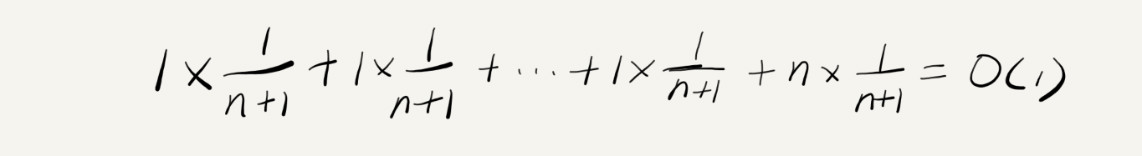
最好时间复杂度是O(1)。
最坏情况时间复杂度：O(n)。
平均时间复杂度：O(1)。
均摊时间复杂度：O(1)。