【ybtoj】【数位dp专题】

前言

假期最后两天不想做什么太难的，就把数位DP开了吧！正好填之前挖的坑

数位DP看起来貌似都比较裸...而且题目简短，注意一下代码的细节就好

本篇记录里全部使用记忆化搜索

记忆化搜索复杂度=状态数*枚举数

目录

• A. 【例题1】B数计数

• B. 【例题2】区间圆数

• C. 【例题3】数字计数

• D. 【例题4】数字整除

• F. 1.幸运数字

• G. 2.幸运666

• H. 3.奶牛编号

题解

A. 【例题1】B数计数

分析：

此题是第一道ybt的数位dp题，引入一些模板的写法

对于所有求1~n，L~R的 xx数 个数的，一般都是从高位到低位搜索，而且记录一个 ok 变量来表示当前数位可不可以随便填数字（每一位数字填完最后不能比 n 大）

由于ok 变量不需要在 dp 数组里记录，可以直接传参到记忆化搜索里，但是ok==0和ok==1时候 dp 数组的记忆化值是不一样的，所以规定只记忆化ok==1（即可以随便填）时的 dp 值，这是因为ok==0的情况很少，所以不用记忆化问题也不大（ps：测试时发现枚举 i 的时候倒序枚举也可以使记忆化不重复，有点玄学，本质是因为先算完了所有ok==0的情况再算ok==1的情况，所以不会重复。但不推荐这么写）

实际上，应该也可以在 dp 数组中记录 ok ，理论上空间会变大一倍（ok取值0，1），但是搜索部分会快一点点

那么回归本题，设计dp状态为 dp[pos][res][op]

pos表示第几位，res表示余数，op表示13数出现的状态（op==0没出现过，op==1上一位是1而且之前没出现过完整的13，op==2表示出现过13），maxn表示当前最大能填的数字，ok表示当前这位是否可以随便填 
(一开始我想用check表示是否出现过13,其实不需要，可以用op代替) ``` #include<bits/stdc++.h> using namespace std; #define ll long long const int INF = 0x3f3f3f3f; int n,dp[11][14][3],dig[11],m,mi[11]; void init() { //memset(dp,-1,sizeof(dp)); //memset(dig,0,sizeof(dig)); m=0; while(n) { int x=n%10; dig[++m]=x; n/=10; } } //可以有前导零，不用记录zero //pos表示第几位，res表示余数，op表示13数出现的状态，maxn表示当前最大能填的数字 //(一开始我想用check表示是否出现过13,其实不需要，可以用op代替) //ok表示当前这位是否可以随便填 int solve(int pos,int res,int op,bool ok) { if(pos==0) return dp[pos][res][op]=(op==2&&res==0); if(dp[pos][res][op]!=-1&&ok) return dp[pos][res][op]; int ret=0,maxn=9; if(!ok) maxn=dig[pos]; for(int i=maxn;i>=0;i--) { int tmp=(res+mi[pos]*i)%13; //分类讨论当前填的数字大小 if(i<maxn) { //if(check) ret+=solve(pos-1,tmp,op,1,1); if(op==2) {ret+=solve(pos-1,tmp,2,1);continue;} if(i==1) ret+=solve(pos-1,tmp,1,1); else if(i==3&&op==1) ret+=solve(pos-1,tmp,2,1); else ret+=solve(pos-1,tmp,0,1); } else { if(op==2) {ret+=solve(pos-1,tmp,2,ok);continue;} if(i==1) ret+=solve(pos-1,tmp,1,ok); else if(i==3&&op==1) ret+=solve(pos-1,tmp,2,ok); else ret+=solve(pos-1,tmp,0,ok); } } // printf("dp[%d][%d][%d]=%d\n",pos,res,op,ret); if(ok) dp[pos][res][op]=ret; return ret; } int main() { mi[1]=1; for(int i=2;i<=10;i++) mi[i]=mi[i-1]*10; while(scanf("%d",&n)!=EOF) { init(); printf("%d\n",solve(m,0,0,0)); } return 0; } /* input: 131312 131313 13333 13332 13338 output: 550 551 60 60 61 */ ```

B. 【例题2】区间圆数

分析：

题目里面要求二进制，那就改成二进制的数位DP就可以啦

这道题目引入了前导零的处理方法：okz 判断前导零是否结束，prezero记录前导零数量

设计 dp[pos][cntzero][prezero] （回去看题解，发现可以压成两维 dp[pos][cntzero]）

pos填到第几位，cntzero填的0数量，prezero前导0数量，maxn当前填的最大数，okz前导0是否结束,okm表示当前这位是否可以随便填 
op表示操作的这个数字是 L 还是 R

---

记忆化的时候不用分别记忆okz==0和okz==1的情况（当然记录也没问题），因为对于一个okz==0的情况，在这个dp状态一定是形如 dp[m-k][k][k]这样的样子，这样的状态不会被okz==1的情况覆盖

（其实如果想不明白就把okz也记忆化，也是没有问题的）

update：最好还是记忆化 okz ， 否则可能因为位数不同而出错（本代码里因为算L，R时都清空了dp数组所以没错），详见下一道题 例题3

代码：

B. 【例题2】区间圆数

```
#include<bits/stdc++.h>
using namespace std;
#define ll long long
const int INF = 0x3f3f3f3f;
int L,R;
int dig[3][35],m[3];
int dp[35][35][35];
inline void init()
{
	//mi[1]=1;
	//for(int i=2;i<=33;i++) mi[i]=mi[i-1]<<1;
	memset(dp,-1,sizeof(dp));
	L--;//忘了这个... 
	while(L)
	{
		int x=L%2;
		dig[1][++m[1]]=x;
		L>>=1;
	}
	while(R)
	{
		int x=R%2;
		dig[2][++m[2]]=x;
		R>>=1;
	}
}

//pos填到第几位，cntzero填的0数量，prezero前导0数量，maxn当前填的最大数，okz前导0是否结束,okm表示当前这位是否可以随便填

//op表示dig[op]...

int solve(int pos,int cntzero,int prezero,int okz,int okm,int op)

{

if(pos0) return cntzero-prezero>=m[op]-cntzero;

if(dp[pos][cntzero][prezero]!=-1&&okm&&okz) return dp[pos][cntzero][prezero];

int ret=0,maxn=1;

if(!okm) maxn=dig[op][pos];

for(int i=0;i<=maxn;i++)

{

if(i<maxn)

{

if(okz) ret+=solve(pos-1,cntzero+(i0),prezero,1,1,op);

else ret+=solve(pos-1,cntzero+(i0),prezero+(i0),i,1,op);

}

else

{

if(okz) ret+=solve(pos-1,cntzero+(i0),prezero,1,okm,op);

else ret+=solve(pos-1,cntzero+(i0),prezero+(i==0),i,okm,op);

}

}

if(okm&&okz) dp[pos][cntzero][prezero]=ret;

return ret;

}

int main()

{

scanf("%d%d",&L,&R);

init();

int ans1=solve(m[1],0,0,0,0,1);

memset(dp,-1,sizeof(dp));

int ans2=solve(m[2],0,0,0,0,2);

printf("%d\n",ans2-ans1);

return 0;

}




</code></pre>
</details>
<h2 class="ui header">C. 【例题3】数字计数</h2>
<p><img src="https://img2020.cnblogs.com/blog/2129610/202108/2129610-20210831145407438-918693718.png" /></p>
<h3>分析：</h3>
<p>做了两道题就会发现，数位DP的套路还是很清晰的</p>
<p>这道题无非就是填数的过程中记录一下某一个数字出现的次数，在边界的时候返回这个次数作为答案</p>
<p>不过需要特殊记录 0 出现的次数，因为要除去前导零的个数，类似<strong>例题2</strong></p>
<p>设计<strong>dp[pos][num][cnt][zero]</strong>&nbsp; （回去看题解，发现实际上<span style="color: #e03e2d;">可以压成两维 <strong>dp[pos][cnt]</strong></span>）</p>
<p>pos表示当前填到第几位，num表示当前计算的数字，cnt表示num的数量，ok判断是否可以随便填，op判断是l还是r<br />okz判断前导零是否结束,zero记录前导零数量&nbsp;</p>
<p>再考虑一下记忆化的问题，这道题和上一道题不一样，必须<span style="color: #e03e2d;">只记忆化 okz==1&amp;&amp;ok==1 的情况，如果不记录 okz 会 90pts WA</span></p>
<p>至于为什么...对于L，R位数不一样的情况，比如：</p>
<p>L：&nbsp; 000</p>
<p>R：0001</p>
<p>此时如果不记忆化 okz ，两个dp值的记忆化就会冲突（因为L：okz==0，R：okz==1）</p>
<h3>代码：</h3>
<details>
<summary>C. 【例题3】数字计数</summary>
<pre class="language-cpp highlighter-hljs" data-dark-theme="true"><code>#include&lt;bits/stdc++.h&gt;
using namespace std;
#define ll long long
const int INF = 0x3f3f3f3f,N = 14;
ll l,r;
int dig[2][N],m[2];
ll dp[N][10][N][N];
//dp[pos][num][cnt]
void init()
{
	memset(dp,-1,sizeof(dp));
	l--;
	while(l)
	{
		int x=l%10;
		dig[0][++m[0]]=x;
		l/=10;
	}
	while(r)
	{
		int x=r%10;
		dig[1][++m[1]]=x;
		r/=10;
	}
}
//pos表示当前填到第几位，num表示当前计算的数字，cnt表示num的数量，ok判断是否可以随便填，op判断是l还是r
//okz判断前导零是否结束,zero记录前导零数量 
ll solve(int pos,int num,int cnt,int ok,int op,int okz,int zero)
{
	//printf("%d\n",(!num)*zero);
	if(!pos) return dp[pos][num][cnt][zero]=cnt-(!num)*zero;//如果num是0，那计数要减去前导零 
	if(dp[pos][num][cnt][zero]!=-1&amp;&amp;ok&amp;&amp;okz) return dp[pos][num][cnt][zero];
	ll ret=0;int maxn=9;
	if(!ok) maxn=dig[op][pos];
	for(int i=0;i&lt;=maxn;i++)
		ret+=solve(pos-1,num,cnt+(i==num),ok||i&lt;maxn,op,okz||i,zero+(!okz&amp;&amp;!i));
	if(ok&amp;&amp;okz) dp[pos][num][cnt][zero]=ret;
	return ret;
}
int main()
{
	scanf("%lld%lld",&amp;l,&amp;r);
	init();
	ll ans1=0,ans2=0;
	for(int i=0;i&lt;=9;i++) 
	{
		ans1=0,ans2=0;
		//memset(dp,-1,sizeof(dp));
		ans1=solve(m[0],i,0,0,0,0,0);
		//memset(dp,-1,sizeof(dp));
		ans2=solve(m[1],i,0,0,1,0,0);
		
		printf("%lld ",ans2-ans1);
	}

	return 0;
}</code></pre>
</details>
<h2 class="ui header">D. 【例题4】数字整除</h2>
<p><img src="https://img2020.cnblogs.com/blog/2129610/202108/2129610-20210831150910188-1757418994.png" /></p>
<h3>分析：</h3>
<p>这道题还是有点小技巧的</p>
<p>首先我们可以很简单地设计出 <strong>dp[pos][res][sum]</strong>，pos表示第几位，res表示余数，sum表示数位之和。但是由于数位之和一直在变（也就是模数一直在变），所以这样记录出来的 res 是无效的</p>
<p>那么我们多枚举一维 mod 表示模数，边界的时候判断 sum 是否==mod就可以啦</p>
<p>再考虑 mod 这一维加在哪里好</p>
<p>本题3000组输入，肯定每次<strong>记忆化搜索</strong>不清空，才不会<span style="color: #e03e2d;">TLE</span>，所以本题中<span style="color: #e03e2d;"> mod 肯定要记录在dp数组里面</span>，空间可以承受</p>
<p>但是洛谷有一道题<a href="https://www.luogu.com.cn/problem/P4127">P4127 [AHOI2009]同类分布</a>，只有一组输入，但是数据范围到了10<sup>18</sup>，那 mod 记录在dp数组里就会<span style="color: #e03e2d;">MLE</span>，不过由于只有一组输入，所以洛谷上只<span style="color: #e03e2d;">在记忆化搜索和主函数里枚举 mod 之后 每次清空</span>就可以了</p>
<p>以上是典型的<span style="color: #e03e2d;">时间换空间</span></p>
<h3>代码：</h3>
<details>
<summary>D. 【例题4】数字整除</summary>
<pre class="language-cpp highlighter-hljs" data-dark-theme="true"><code>#include&lt;bits/stdc++.h&gt;
using namespace std;
#define ll long long
const int INF = 0x3f3f3f3f;
int L,R;
int dig[3][12],m[3],mi[11];
int dp[12][100][100][100];
//复杂度：1e6...... 
//dp[pos][res][sum][mod] 
inline void init()
{
	m[1]=m[2]=0;
	L--;//忘了这个... 
	while(L)
	{
		int x=L%10;
		dig[1][++m[1]]=x;
		L/=10;
	}
	while(R)
	{
		int x=R%10;
		dig[2][++m[2]]=x;
		R/=10;
	}
	
} 
//op判断是L还是R 
int solve(int pos,int res,int sum,int mod,bool ok,int op)
{
	if(sum&gt;mod) return dp[pos][res][sum][mod]=0;
	if(pos==0) return dp[pos][res][sum][mod]=(!res&amp;&amp;mod==sum);
	if(ok&amp;&amp;dp[pos][res][sum][mod]!=-1) return dp[pos][res][sum][mod];
	int ret=0,maxn=9;
	if(!ok) maxn=dig[op][pos];
	for(int i=0;i&lt;=maxn;i++)
	{
		int tmp=(res+i*mi[pos])%mod;
		ret+=solve(pos-1,tmp,sum+i,mod,ok||(i&lt;maxn),op);
	}
	if(ok) dp[pos][res][sum][mod]=ret; 
	return ret;
}
int main()
{
	mi[1]=1;
	for(int i=2;i&lt;=10;i++) mi[i]=mi[i-1]*10;
	memset(dp,-1,sizeof(dp));
	while(scanf("%d%d",&amp;L,&amp;R)!=EOF)
	{
		init();
		int ans1=0,ans2=0;
		for(int mod=1;mod&lt;=95;mod++)
			ans1+=solve(m[1],0,0,mod,0,1);
		//memset(dp,-1,sizeof(dp));
		for(int mod=1;mod&lt;=95;mod++)
			ans2+=solve(m[2],0,0,mod,0,2);
		//printf("ans1=%d,ans2=%d\n",ans1,ans2);
		printf("%d\n",ans2-ans1);
	}
	return 0;
}
/*
11 819
11 459
20 743
18 725
9 920
13 877
15 932
6 454
10 533
16 547
*/ </code></pre>
</details><details>
<summary>P4127 [AHOI2009]同类分布</summary>
<pre class="language-cpp highlighter-hljs" data-dark-theme="true"><code>#include&lt;bits/stdc++.h&gt;
using namespace std;
#define ll long long
const int INF = 0x3f3f3f3f;
ll L,R;
int dig[3][20],m[3];
ll mi[20];
ll dp[20][200][200];
//复杂度：1e6...... 
//dp[pos][res][sum][mod] 
inline void init()
{
	m[1]=m[2]=0;
	L--;//忘了这个... 
	while(L)
	{
		int x=L%10;
		dig[1][++m[1]]=x;
		L/=10;
	}
	while(R)
	{
		int x=R%10;
		dig[2][++m[2]]=x;
		R/=10;
	}
	
} 
//op判断是L还是R 
int solve(int pos,int res,int sum,int mod,bool ok,int op)
{
	if(sum&gt;mod) return dp[pos][res][sum]=0;
	if(pos==0) return dp[pos][res][sum]=(!res&amp;&amp;mod==sum);
	if(ok&amp;&amp;dp[pos][res][sum]!=-1) return dp[pos][res][sum];
	int ret=0,maxn=9;
	if(!ok) maxn=dig[op][pos];
	for(int i=0;i&lt;=maxn;i++)
	{
		int tmp=(res+mi[pos]%mod*i)%mod;
		ret+=solve(pos-1,tmp,sum+i,mod,ok||(i&lt;maxn),op);
	}
	if(ok) dp[pos][res][sum]=ret; 
	return ret;
}
int main()
{
	mi[1]=1;
	for(int i=2;i&lt;=19;i++) mi[i]=mi[i-1]*10;
	memset(dp,-1,sizeof(dp));
	scanf("%lld%lld",&amp;L,&amp;R);
	{
		init();
		ll ans1=0,ans2=0;
		for(int mod=1;mod&lt;=200;mod++)
		{
			ans1+=solve(m[1],0,0,mod,0,1);
			memset(dp,-1,sizeof(dp));
		}
		for(int mod=1;mod&lt;=200;mod++)
		{
			ans2+=solve(m[2],0,0,mod,0,2);
			memset(dp,-1,sizeof(dp));
		}
		//printf("ans1=%d,ans2=%d\n",ans1,ans2);
		printf("%lld\n",ans2-ans1);
	}
	return 0;
}
/*
11 819
11 459
20 743
18 725
9 920
13 877
15 932
6 454
10 533
16 547
*/ </code></pre>
</details>
<h2 class="ui header">F. 1.幸运数字</h2>
<p><img src="https://img2020.cnblogs.com/blog/2129610/202108/2129610-20210831152500490-662137510.png" /></p>
<h3>分析：</h3>
<p>妥妥的<strong>例题1</strong>的弱化版，信心题</p>
<p>不过刚看到这个数据范围还吓了一跳，N这么大都输入不进去，难道要高精？</p>
<p>想到高精之后发现除了字符串输入，没有任何别的操作了，这也告诉我们N的大小不重要，因为预处理的时候都要拆成一位一位的</p>
<p>dp状态把<strong>例题1</strong>削弱一下就出来了</p>
<h3>代码：</h3>
<details>
<summary>F. 1.幸运数字</summary>
<pre class="language-cpp highlighter-hljs" data-dark-theme="true"><code>#include&lt;bits/stdc++.h&gt;
using namespace std;
#define ll long long
const int INF = 0x3f3f3f3f;
ll L,R;
int dig[3][20],m[3];
ll mi[20];
ll dp[20][200][200];
//复杂度：1e6...... 
//dp[pos][res][sum][mod] 
inline void init()
{
	m[1]=m[2]=0;
	L--;//忘了这个... 
	while(L)
	{
		int x=L%10;
		dig[1][++m[1]]=x;
		L/=10;
	}
	while(R)
	{
		int x=R%10;
		dig[2][++m[2]]=x;
		R/=10;
	}
	
} 
//op判断是L还是R 
int solve(int pos,int res,int sum,int mod,bool ok,int op)
{
	if(sum&gt;mod) return dp[pos][res][sum]=0;
	if(pos==0) return dp[pos][res][sum]=(!res&amp;&amp;mod==sum);
	if(ok&amp;&amp;dp[pos][res][sum]!=-1) return dp[pos][res][sum];
	int ret=0,maxn=9;
	if(!ok) maxn=dig[op][pos];
	for(int i=0;i&lt;=maxn;i++)
	{
		int tmp=(res+mi[pos]%mod*i)%mod;
		ret+=solve(pos-1,tmp,sum+i,mod,ok||(i&lt;maxn),op);
	}
	if(ok) dp[pos][res][sum]=ret; 
	return ret;
}
int main()
{
	mi[1]=1;
	for(int i=2;i&lt;=19;i++) mi[i]=mi[i-1]*10;
	memset(dp,-1,sizeof(dp));
	scanf("%lld%lld",&amp;L,&amp;R);
	{
		init();
		ll ans1=0,ans2=0;
		for(int mod=1;mod&lt;=200;mod++)
		{
			ans1+=solve(m[1],0,0,mod,0,1);
			memset(dp,-1,sizeof(dp));
		}
		for(int mod=1;mod&lt;=200;mod++)
		{
			ans2+=solve(m[2],0,0,mod,0,2);
			memset(dp,-1,sizeof(dp));
		}
		//printf("ans1=%d,ans2=%d\n",ans1,ans2);
		printf("%lld\n",ans2-ans1);
	}
	return 0;
}
/*
11 819
11 459
20 743
18 725
9 920
13 877
15 932
6 454
10 533
16 547
*/ </code></pre>
</details>
<h2 class="ui header">G. 2.幸运666</h2>
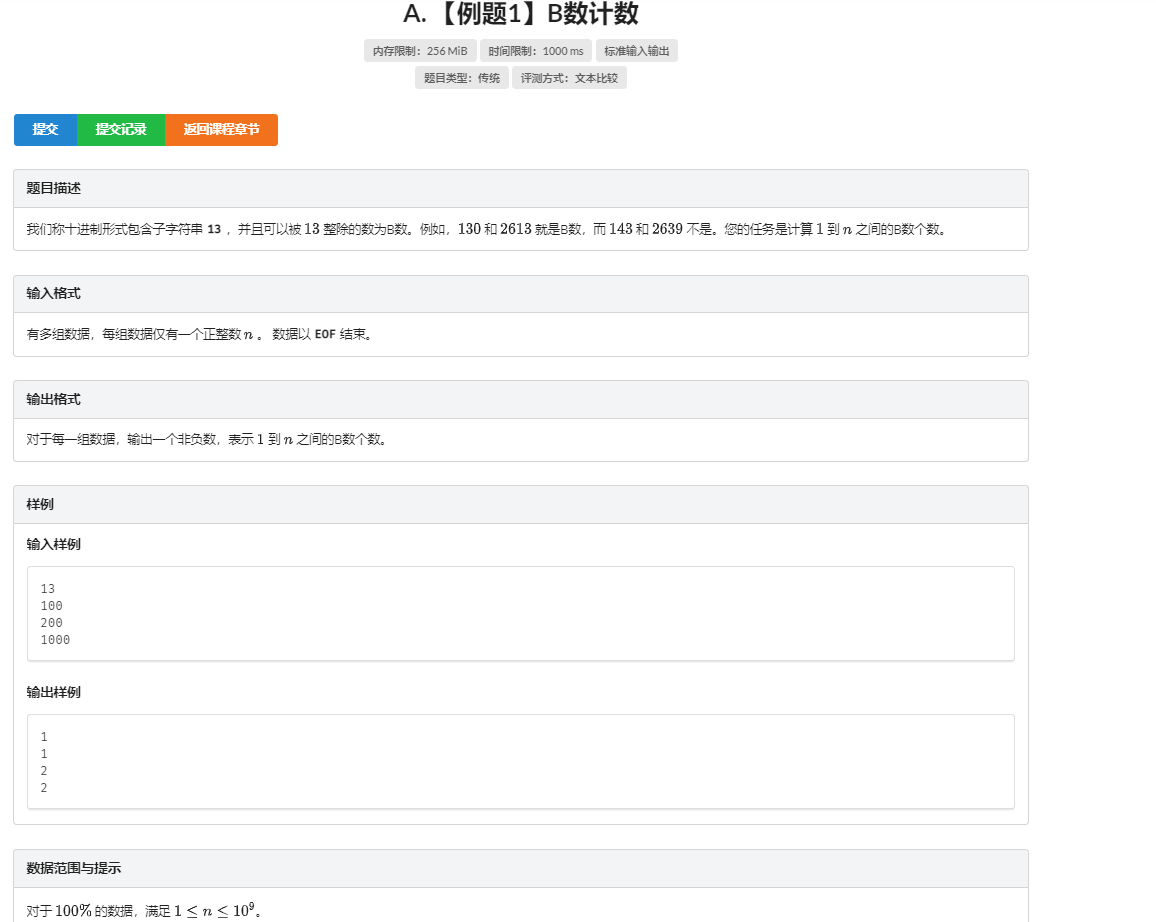
<p>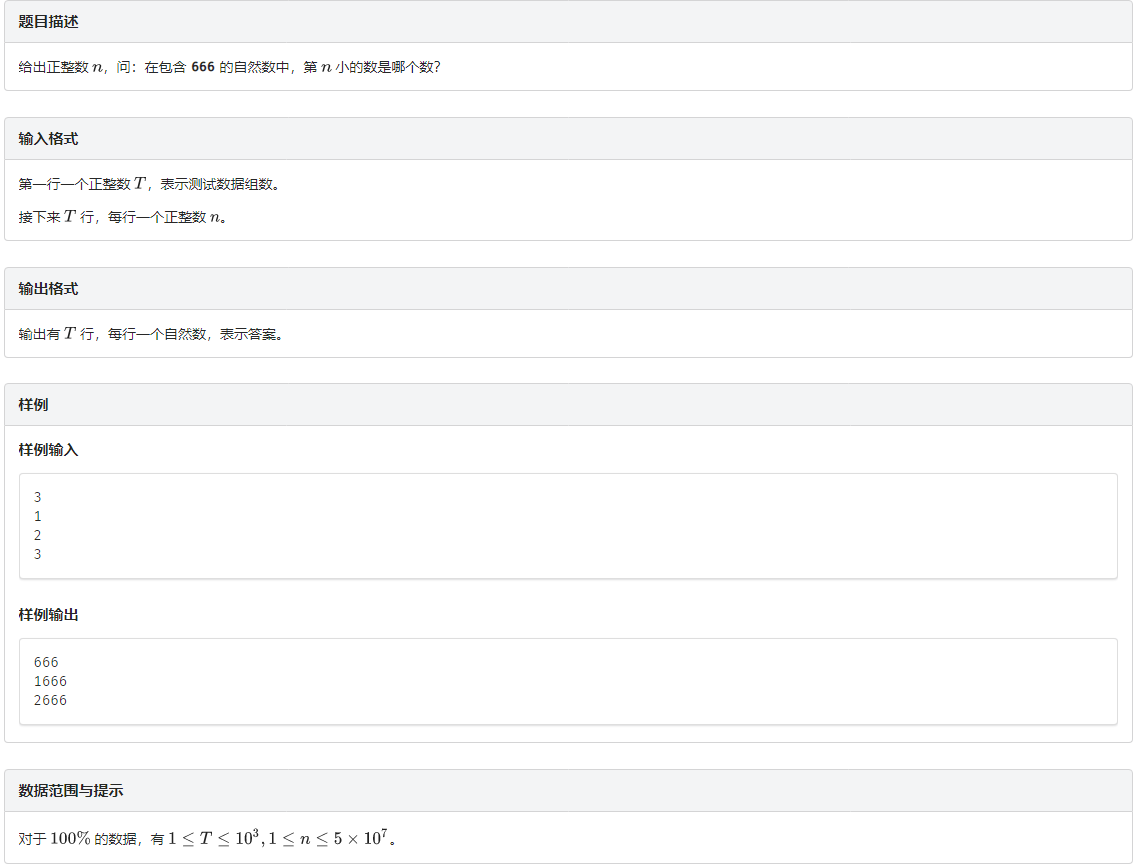![image](https://img2020.cnblogs.com/blog/2129610/202109/2129610-20210917192328130-1670009069.png) ### 分析： 此题引入数位 DP 解决的一种新类型题：求数位符合某种条件第 $k$ 小的数。 设 $f(i,0/1/2)$ 表示由 $i$ 位数字组成的，当前有 $0/1/2$ 个数字 $6$ 连续的非幸运数的个数。 $f(i,3)$ 表示由 $i$ 位数字组成的幸运数的个数。 这个式子就不必记忆化搜索了，直接递推就很简单。 然后可以根据 $f(i,3)$ 推出答案的位数，为最小的 $i$ ，使得 $n\le f(i,3)$。 然后从高位到低位尝试填数，根据预处理出的 $f$ 数组计算剩下的位置有多少种填法，记为 $cnt$. 若 $cnt&lt;n$ ，则说明当前位置填 $j$ 时最大的幸运数一定小于答案，所以``n-=cnt``. 若 $cnt\ge n$，则说明答案的当前位置**必定**填 $j$ ，输出 $j$ 并且接着考虑下一位 $i+1$。 对于最高位数，预计 $10$ 位的时候大概就够 $5 \times 10^7$，但是毕竟是估算还是开大一点范围（代码中开了 $20$） ### 代码: ```cpp #include&lt;bits/stdc++.h&gt; using namespace std; #define ll long long const int INF = 0x3f3f3f3f,N = 5e7+10; int T,n,m; int f[21][4]; void init() { f[0][0]=1; for(int i=1;i&lt;=20;i++) { f[i][0]=9*(f[i-1][0]+f[i-1][1]+f[i-1][2]); f[i][1]=f[i-1][0]; f[i][2]=f[i-1][1]; f[i][3]=10*f[i-1][3]+f[i-1][2]; } } int main() { init(); scanf("%d",&amp;T); while(T--) { scanf("%d",&amp;n); //init(); for(int i=1;i&lt;=20;i++) if(f[i][3]&gt;=n) {m=i;break;} ll cnt=0,k=0; for(int i=m;i&gt;=1;i--) { for(int j=0;j&lt;=9;j++) { cnt=f[i-1][3]; if(k==3) cnt+=f[i-1][0]+f[i-1][1]+f[i-1][2]; else if(j==6) for(int x=3-k-1;x&lt;3;x++) cnt+=f[i-1][x]; if(cnt&lt;n) n-=cnt; else { if(k&lt;3) { if(j==6) k++; else k=0; } printf("%d",j); break; } } } printf("\n"); } return 0; } ``` ## H. 3.奶牛编号 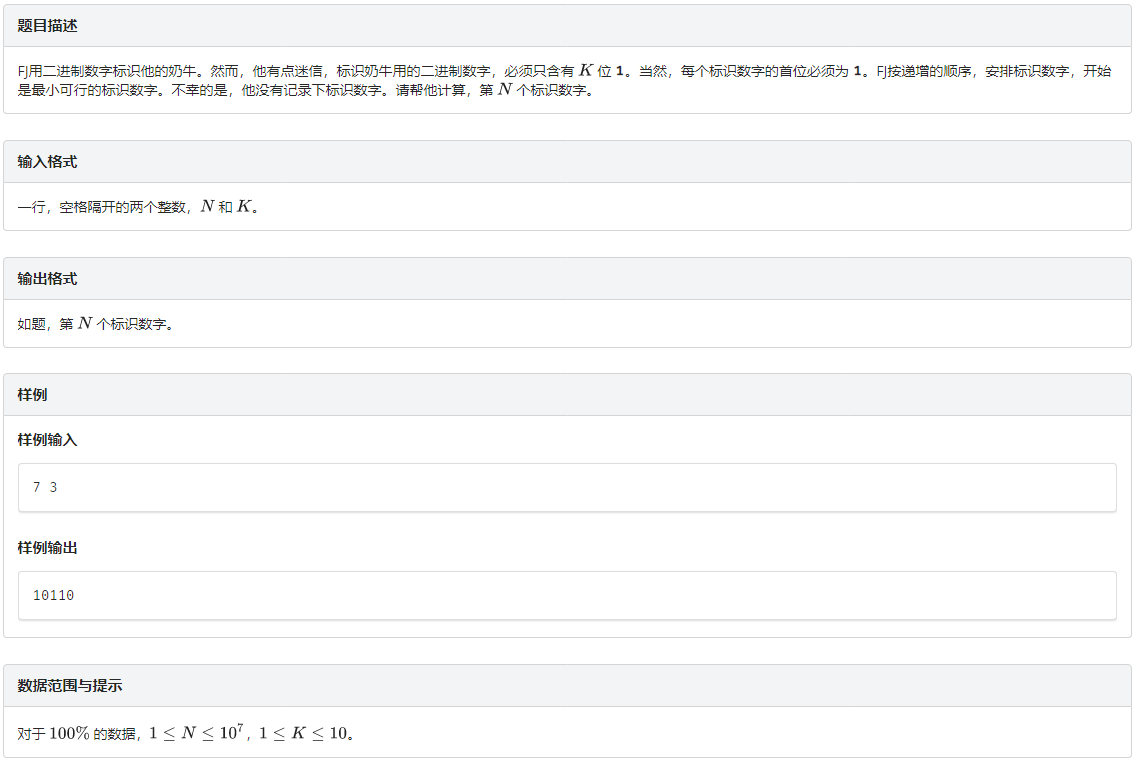![image](https://img2020.cnblogs.com/blog/2129610/202109/2129610-20210917225248957-452098905.png) ### 分析： 设 $f(i,j)$ 表示在前 $i$ 位上放 $j$ 个 $1$ 的方案数，转移很显然：$f(i,j)=f(i-1,j)+f(i-1,j-1)$. 和上一道题一样，从最高位开始填数，对于当前的第 $i$ 个位置，可以填 $0,1$ 。 记 $sumk$ 为能填 $1$ 的个数，$i$ 为当前位。 若 $f(i-1,sumk)&lt;n$ ，则说明当前位如果填 $0$ ，**最大的编号**也**小于** $n$ 。因此当前位**必定**填 $1$ ，同时 ``sumk--,n-=f[i-1][sumk]``. 否则说明当前位填 $0$ 的情况的**最大排名** $\ge n$ ，因此当前位**必定**填 $0$ ，如果当前他填的这个 $0$ 不是前导零就输出。 **注意**：特判``k==1``的情况直接输出 $n$ 位，其余情况**最大**的位数不超过 $5000$. 证明：显然能填的数字 $1$ 越多，最大的位数就越小。考虑``k==2``的情况，最大排名 $N=C^2_n$，即在 $n$ 位数里选两个，根据组合数的公式可以知道 $5000 \times (5000-1) \div 2 &gt; 10^7$ ，所以上界约为 $5000$ ，证毕 ### 代码： ```cpp #include&lt;bits/stdc++.h&gt; using namespace std; #define ll long long const int INF = 0x3f3f3f3f,N = 1e7+10; int n,k,m; ll f[6005][11]; bool fir; void init() { f[0][0]=1; //for(int i=0;i&lt;=6000;i++) f[i][0]=1; for(int i=1;i&lt;=6000;i++) for(int j=0;j&lt;=k;j++) { if(j) f[i][j]=min((ll)1e7,f[i-1][j-1]+f[i-1][j]); else f[i][j]=min((ll)1e7,f[i-1][j]); //printf("dp[%d][%d]=%d\n",i,j,f[i][j]); } } //书上写dfs输出答案，但没必要，直接按照下面i从m-&gt;1的循环输出即可 void dfs(int x,int y,int stp) { if(!stp) return; if(x&gt;f[stp-1][y]) { printf("1"); fir=1; dfs(x-f[stp-1][y],y-1,stp-1); } else { if(fir) printf("0"); dfs(x,y,stp-1); } } int main() { scanf("%d%d",&amp;n,&amp;k); init(); for(int i=1;i&lt;=6000;i++) if(f[i][k]&gt;=n) {m=i;break;} //printf("m=%d\n",m); if(k==1) { for(int i=1;i&lt;=n;i++) if(i==1) printf("1"); else printf("0"); return 0; } //dfs(n,k,6000); int sumk=k; for(int i=m;i&gt;=1;i--) { if(f[i-1][sumk]&lt;n) { printf("1"); n-=f[i-1][sumk]; sumk--,fir=1; } else if(fir) printf("0"); } return 0; } ```</p>