题解：P14799 [JOI 2026 二次预选] 比太郎之旅 3 / Bitaro's Travel 3

set 吗？？？bitset 无敌！！！

recall.cpp

题意？

一个无向图，选择一条路径，使得奇数号位的编号小于下一位，偶数号位的编号大于下一位。

对每个点，求出以他为起点的所有路径都不包含的点个数。

建图

显然双层图。

对于每条边 \((u,v)\)，保证 \(u<v\)，连一条 \((u_1,v_2)\) 的无向边。

每次从 \(s_1\) 出发，与他联通的点都可达。

以样例 #4 为例

6 6
1 4
1 3
2 4
2 5
3 6
5 6

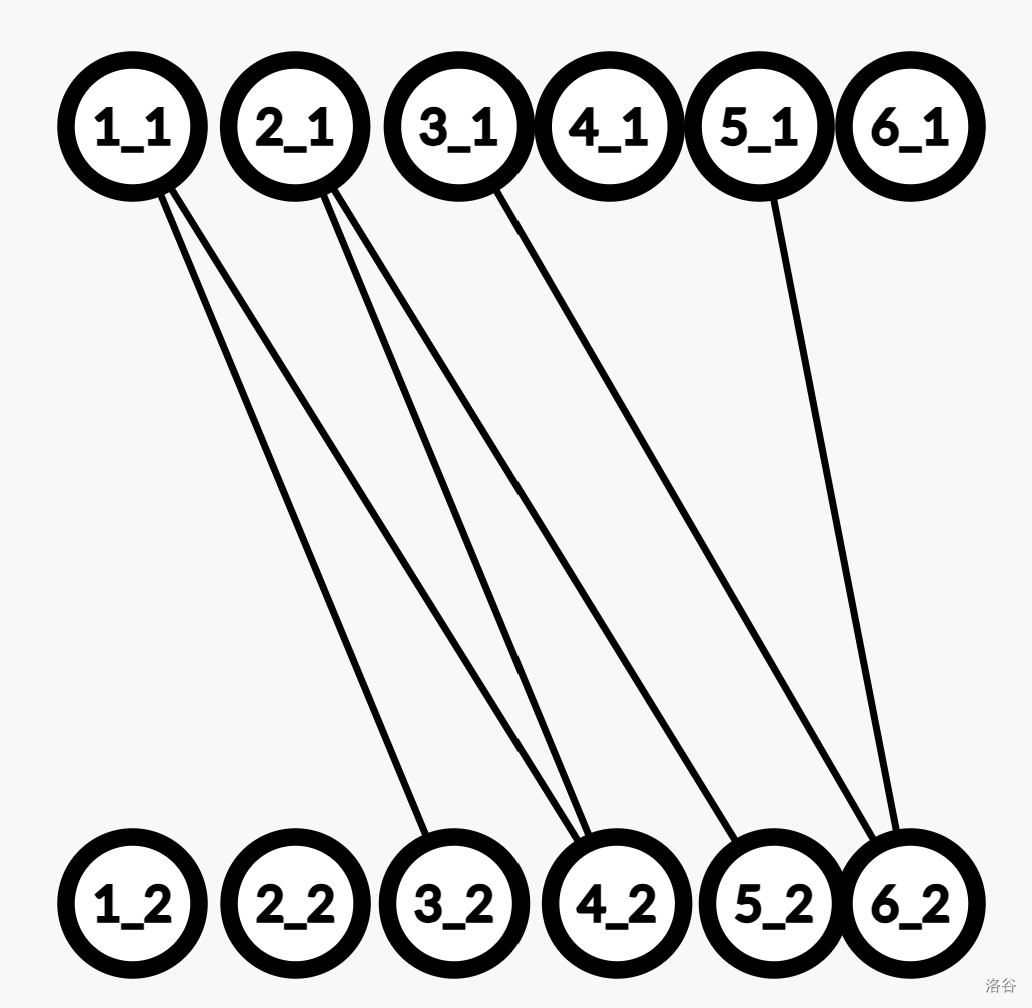
\(1\) 为起点可达点集为 \(\{1,2,3,4,5\}\)；
\(2\) 为起点可达点集为 \(\{1,2,3,4,5\}\)；
\(3\) 为起点可达点集为 \(\{3,5,6\}\)；
\(4\) 为起点可达点集为 \(\{4\}\)；
\(5\) 为起点可达点集为 \(\{3,5,6\}\)；
\(6\) 为起点可达点集为 \(\{6\}\)。

PS：起点必须是第一层，可达点只关注编号。

即：同连通块的点互相可达。

解决

对每个起点 dfs 一遍，记下连通块编号，并记下块内编号数量。

问题来了：怎么计数？（\(u_1\) 和 \(u_2\) 视为同一个点）

set：我来 \(O(\log n)\) 存点。

bitset：你好。

:::info[bitset]{open}
\(O(\frac {n(n-m)}{ \omega})\)

记录

实则极限 \(n=300 000,m=0\) 的数据跑了 \(7.02s\)。

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=6e5+5;
int n,m;
vector<int> g[N];
int scc[N],tot;
bitset<N> b;
vector<int> v;
int ans[N];
void dfs(int u){
	scc[u]=tot;
	if(u>n)	b[u-n]=1;
	else	b[u]=1,v.push_back(u);
	for(int i=0;i<g[u].size();i++){
		int v=g[u][i];
		if(scc[v])	continue;
		dfs(v);
	}
	return;
}
signed main(){
	cin>>n>>m;
	for(int i=1;i<=m;i++){
		int u,v;
		cin>>u>>v;
		g[u].push_back(v+n);
		g[v+n].push_back(u);
	}
	for(int i=1;i<=n;i++){
		if(scc[i])	continue;
		tot++;
		v.clear();
		b.reset();
		dfs(i);
		int res=b.count();
		for(int i=0;i<v.size();i++)
			ans[v[i]]=n-res;
	}
	for(int i=1;i<=n;i++)
		cout<<ans[i]<<'\n';
	return 0;
}

:::

:::info[set]{open}
\(O(n \log m)\)

记录

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=6e5+5;
int n,m;
vector<int> g[N];
int scc[N],tot;
set<int> b;
vector<int> v;
int ans[N];
void dfs(int u){
	scc[u]=tot;
	if(u>n)	b.insert(u-n);
	else	b.insert(u),v.push_back(u);
	for(int i=0;i<g[u].size();i++){
		int v=g[u][i];
		if(scc[v])	continue;
		dfs(v);
	}
	return;
}
signed main(){
	ios::sync_with_stdio(0);
	cin.tie(0),cout.tie(0);
	cin>>n>>m;
	for(int i=1;i<=m;i++){
		int u,v;
		cin>>u>>v;
		g[u].push_back(v+n);
		g[v+n].push_back(u);
	}
	for(int i=1;i<=n;i++){
		if(scc[i])	continue;
		tot++;
		v.clear();
		b.clear();
		dfs(i);
		int res=b.size();
		for(int i=0;i<v.size();i++)
			ans[v[i]]=n-res;
	}
	for(int i=1;i<=n;i++)
		cout<<ans[i]<<'\n';
	return 0;
}

:::

完结撒花