题解：P2076 曼哈顿距离最小生成树

曼哈顿距离最小生成树

声明

本篇题解主要是 FFTotoro 大佬的思想，但由于他的代码过于高深，本人发一篇易懂的题解 233。

食用者记得先看 FFTotoro 大佬的题解，再 copy 欣赏易懂代码。

思想

Kruskal 算法 emm，与边数直接挂钩，因此完全图直接跑 Kruskal 是不理智的。

考虑到大部分边是无用的，所以用人类智慧思考哪些边有用。

结论：以一个点为原点建立直角坐标系，在每 45 度内只会向距离该点最近的一个点连边。

简单证明一下，如图，当 \(x_1+y_1<x_2+y_2\) 时，原点与 \((x_2,y_2)\) 的曼哈顿距离必定最大，是无用的，丢掉。

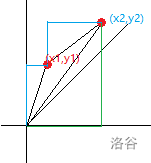
实际考虑

为了避免重复加边，我们只考虑左半边这4个区域。

设最近点为 \((x,y)\)，则对于任意该区域内其他点 \((x_i,y_i)\)，有：

• 如果点在 R1，它要满足：\(x \ge x_i ,y - x \ge y_i - x_i\)；
• 如果点在 R2，它要满足：\(y \ge y_i ,y - x \le y_i - x_i\)；
• 如果点在 R3，它要满足：\(y \le y_i ,y + x \ge y_i + x_i\)；
• 如果点在 R4，它要满足：\(x \ge x_i ,y + x \le y_i – x_i\)。

FFTotoro 大佬是用对称性变化的，本蒟蒻认为不太好理解，于是把每种情况列出来。

观察第一限制，是区间最值问题，并且一定是前缀最值，用树状数组非常方便维护。代码中只维护最小值，此时后缀即是最大值。

第二限制交给排序了。

复杂度

建图，包括排序及树状数组：\(O(n \log n)\)；

Kruskal，共建 \(m=4n\) 条边：\(O(m \log m)\)。

在 \(n\le2 \times 10^5\) 的范围内可以通过。

code

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=2e5+5;
const int inf=1e18;

struct BIT{					//树状数组 
	pair<int,int> a[N<<1];
	int n;
	inline int lowbit(int x){
		return x&-x;
	}
	void init(int _){
		n=_;
		for(int i=1;i<=n;i++)
			a[i]=make_pair(inf,0);
		return;
	}
	pair<int,int> qry(int x){
		pair<int,int> res=make_pair(inf,0);
		for(;x;x-=lowbit(x))
			res=min(res,a[x]);
		return res;
	}
	void upd(int x,pair<int,int> v){
		for(;x<=n;x+=lowbit(x)){
			a[x]=min(a[x],v);
		}
		return;
	}
	pair<int,int> qry_frt(int x){	//询问前缀，返回最小 
		return qry(x);
	}
	pair<int,int> qry_bck(int x){	//询问后缀，返回最大 
		return qry(n-x+1);
	}
	void upd_frt(int x,pair<int,int> v){
		return upd(x,v);
	}
	void upd_bck(int x,pair<int,int> v){
		return upd(n-x+1,v);
	}
}tr;

int n;
struct node{
	int x,y;
	int ix,iy;	//离散后 
	int id;
	int d,s;	//d 表示 y-x，s 表示 x+y 
}p[N];
int st[N<<2],tot;


int getdis(int x,int y){	//曼哈顿距离 
	return abs(p[x].x-p[y].x)+abs(p[x].y-p[y].y);
}

struct edge{		//存边 
	int u,v,w;
	bool operator <(const edge& p) const{
		return this->w<p.w;
	}
}e[N<<2];
int cnt;

bool cmp1(node a,node b){	//4种区域 
	return a.d>b.d||(a.d==b.d&&a.x>b.x);
//	if(a.d==b.d)	return a.x>b.x;
//	return a.d>b.d;
}
bool cmp2(node a,node b){
	return a.d<b.d||(a.d==b.d&&a.x>b.x);
//	if(a.d==b.d)	return a.x>b.x;
//	return a.d<b.d;
}
bool cmp3(node a,node b){
	return a.s>b.s||(a.s==b.s&&a.y<b.y);
//	if(a.s==b.s)	return a.y<b.y;
//	return a.s>b.s;
}
bool cmp4(node a,node b){
	return a.s<b.s||(a.s==b.s&&a.y>b.y);
//	if(a.s==b.s)	return a.y>b.y;
//	return a.s<b.s;
}

void make_G(){	//建图 
	tr.init(2*n);	//初始化很重要 
	sort(p+1,p+1+n,cmp1);
	for(int i=1;i<=n;i++){
		pair<int,int> t=tr.qry_bck(p[i].ix);
		if(t.first<inf)	
			e[++cnt].u=p[i].id,e[cnt].v=p[t.second].id,e[cnt].w=getdis(i,t.second);
		tr.upd_bck(p[i].ix,make_pair(p[i].s,i)); 
	}
	
	tr.init(2*n);
	sort(p+1,p+1+n,cmp2);
	for(int i=1;i<=n;i++){
		pair<int,int> t=tr.qry_bck(p[i].iy);
		if(t.first<inf)	
			e[++cnt].u=p[i].id,e[cnt].v=p[t.second].id,e[cnt].w=getdis(i,t.second);
		tr.upd_bck(p[i].iy,make_pair(p[i].s,i)); 
	}
	
	tr.init(2*n);
	sort(p+1,p+1+n,cmp3);
	for(int i=1;i<=n;i++){
		pair<int,int> t=tr.qry_frt(p[i].ix);
		if(t.first<inf)	
			e[++cnt].u=p[i].id,e[cnt].v=p[t.second].id,e[cnt].w=getdis(i,t.second);
		tr.upd_frt(p[i].ix,make_pair(p[i].d,i)); 
	}
	
	tr.init(2*n);
	sort(p+1,p+1+n,cmp4);
	for(int i=1;i<=n;i++){
		pair<int,int> t=tr.qry_bck(p[i].iy);
		if(t.first<inf)	
			e[++cnt].u=p[i].id,e[cnt].v=p[t.second].id,e[cnt].w=getdis(i,t.second);
		tr.upd_bck(p[i].iy,make_pair(p[i].d,i)); 
	}
	
	return;
}

int fa[N];		//路径压缩并查集 
int find(int x){
	if(fa[x]==x)	return x;
	return fa[x]=find(fa[x]);
}

signed main(){
	cin>>n;
	for(int i=1;i<=n;i++){
		cin>>p[i].x>>p[i].y;
		p[i].id=i;
		p[i].d=p[i].y-p[i].x;
		p[i].s=p[i].x+p[i].y;
	}
	
	for(int i=1;i<=n;i++){		//离散化：树状树状用的 
		st[++tot]=p[i].x;
		st[++tot]=p[i].y;
	}
	sort(st+1,st+1+tot);
	for(int i=1;i<=n;i++){
		p[i].ix=lower_bound(st+1,st+1+tot,p[i].x)-st;
		p[i].iy=lower_bound(st+1,st+1+tot,p[i].y)-st;
	}
	
	make_G();
	
	for(int i=1;i<=n;i++)		//Kruskal 
		fa[i]=i;
	sort(e+1,e+1+cnt);
	int k=0,ans=0;
	vector<int> V;
	for(int i=1;i<=cnt;i++){
		int u=e[i].u,v=e[i].v;
		u=find(u),v=find(v);
		if(u==v)	continue;
		ans+=e[i].w;
		V.push_back(i);
		fa[u]=v;
		k++;
		if(k==n-1)	break;
	}
	
	cout<<ans<<'\n';
	for(int i=0;i<V.size();i++)
		cout<<e[V[i]].u<<' '<<e[V[i]].v<<'\n';
	return 0;
}