CF645D 题解——from BTJ

CF645D 题解

啥玩意儿？并查集？——from 蒟蒻 BTJ

二分答案+拓扑排序

设机器人 \(u\) 打败机器人 \(v\)。

则建立一条自 \(u\) 向 \(v\) 的有向边。

二分边数 \(m\)，剩下的交给 topo 板板。

复杂度 \(O(n\log n)\)，刚好 haha。

拓扑排序

基本的步骤：

计算每个点的入度。

• 入度为 \(0\) 就加入队列。

• 当队列不为空则循环：

  • 取出队首元素并输出。

  • 遍历队首元素的连边，对应节点的入度 \(−1\)。

  • 当对应的节点入度为 \(0\) 就加入队列。

——from LV06 巨佬的博客 OZR。

样例解释

四条边：

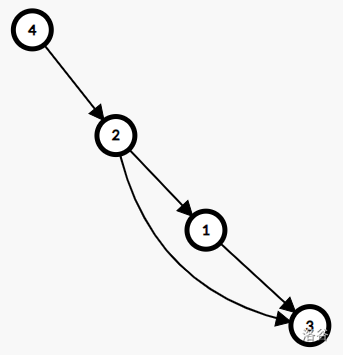
五条边：

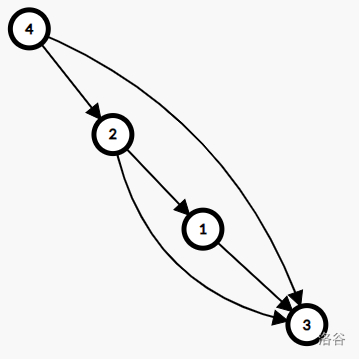
可见四条边即可。

CODE:

#include<iostream>
#include<vector>
#include<queue>
#include<cstring>
#define int long long
const int N=1e5+5;
int n,m;
std::pair<int,int> p[N];
std::queue<int> q;
std::vector<int> e[N];
bool vis[N];
int in[N];
bool check(int x){
	memset(in,0,sizeof(in));
	memset(vis,false,sizeof(vis));
	while(!q.empty())	q.pop();
	for(int i=0;i<N;i++)	e[i].clear();
	for(int i=1;i<=x;i++){
		e[p[i].first].push_back(p[i].second);
		in[p[i].second]++;
	}
	for(int i=1;i<=n;i++){
		if(in[i])	continue;
		vis[i]=true;
		q.push(i);
	}
	while(!q.empty()){
		if(q.size()>1)	return false;
		int u=q.front();
		q.pop();
		for(std::vector<int>::iterator it=e[u].begin();it!=e[u].end();it++){
			in[*it]--;
			if(!in[*it]&&!vis[*it]){
				vis[*it]=1;
				q.push(*it);
			}
		}
	}
	return true;
}
signed main(){
	std::ios::sync_with_stdio(0);
	std::cin.tie(0),std::cout.tie(0);
	std::cin>>n>>m;
	for(int i=1;i<=m;i++){
		int u,v;
		std::cin>>u>>v;
		p[i]=std::make_pair(u,v);
	}
	int l=1,r=m;
	bool f=false;
	while(l<=r){
		int mid=l+r>>1;
		if(check(mid))	r=mid-1,f=1;
		else	l=mid+1;
	}
	if(f)	std::cout<<r+1;
	else	std::cout<<-1;
	return 0;
}

后记

本来真打算打并查集的，后来发现太长太难打，就不打惹。

有没有巨佬打个并查集让我涨涨见识。

完结撒花~