鸢尾花书 - Book_3《数学要素》 - Chapter13 二元函数

13.1 二元一次函数：平面

二元一次函数是一元一次函数的扩展：
\(y = f(x_{1}, x_{2}) = w_{1}x_{1} + w_{2}x_{2} + b\) 后面简称（1）
当w1和w2均为0时，\(f(x_{1}, x_{2}) = b\)为二元常数函数，平行于x1x2水平面

用矩阵乘法，（1）可以写成：
\(y = f(x_{1}, x_{2}) = w^{T}x + b\)（2）
其中：
\(\boldsymbol{w} = \begin{bmatrix}w_{1} \\w_{2}\end{bmatrix},\boldsymbol{x} = \begin{bmatrix}x_{1} \\x_{2}\end{bmatrix}\) 后面简称（3）
当y取一定值时，比如y=c，平面退化为一条直线：\(w_{1}x_{1} + w_{2}x_{2} + b = c\)

从另外一个角度，c相当于\(f(x_{1}, x_{2})\)平面的某一条等高线，即\(f(x_{1}, x_{2})\)等高线为直线

举个例子1

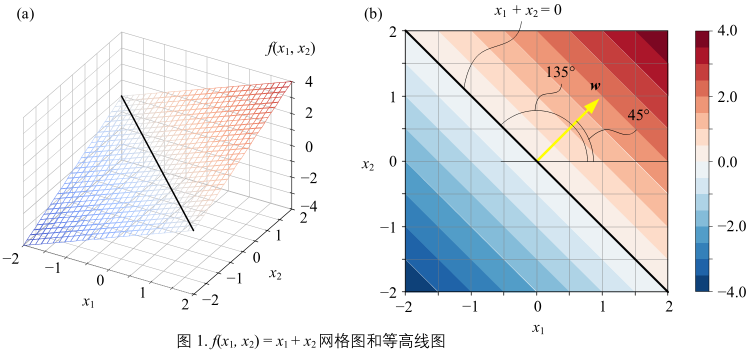
图1：
解析式：
\( y = f(x_{1},x_{2}) = x_{1} + x_{2} = \underbrace{\begin{bmatrix} 1\\1 \end{bmatrix}^{T}}_{\text{w}} \underbrace{\begin{bmatrix} x_{1}\\x_{2} \end{bmatrix}}_{\text{x}} \)（5）

图1（a）
所示为（5）的对应平面，图中黑色直线对应x1 + x2 = 0，即 x2 = -x1。

图1（b）
所示\(f(x_{1}, x_{2})\)平面等高线都平行于x1 + x2 = 0。由于\(f(x_{1}, x_{2})\)为线性函数，因此等高线平行，且间距相同。

图1（b）
黄色箭头为\(f(x_{1}, x_{2})\)增大方向，箭头和x1轴正方向夹角为45°。黄色箭头对应的向量就是 w：\(\boldsymbol{w} = \begin{bmatrix} 1\\1 \end{bmatrix}\)

图1（b）
w 向量垂直于等高线并指向\(f(x_{1}, x_{2})\)增大方向，w向量便是梯度向量。

举个例子2

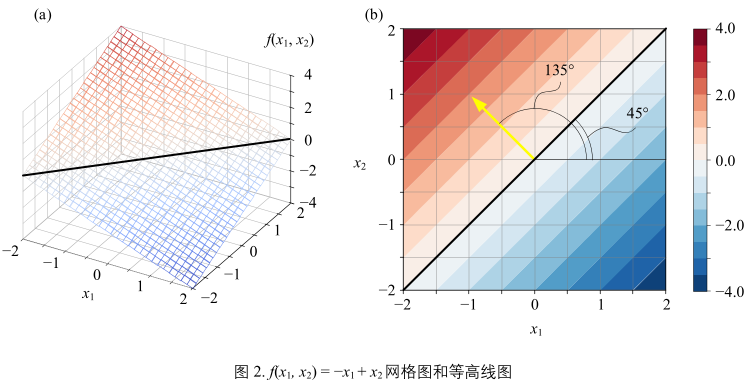
\( y = f(x_{1},x_{2}) = -x_{1} + x_{2} = \underbrace{\begin{bmatrix} -1\\1 \end{bmatrix}^{T}}_{\text{w}} \underbrace{\begin{bmatrix} x_{1}\\x_{2} \end{bmatrix}}_{\text{x}} \)（7）

图2（b）
黄箭头同样指向\(f(x_{1}, x_{2})\)增大方向，对应（7）中的w。箭头和x1轴正方向夹角为135°

等高线平行纵轴

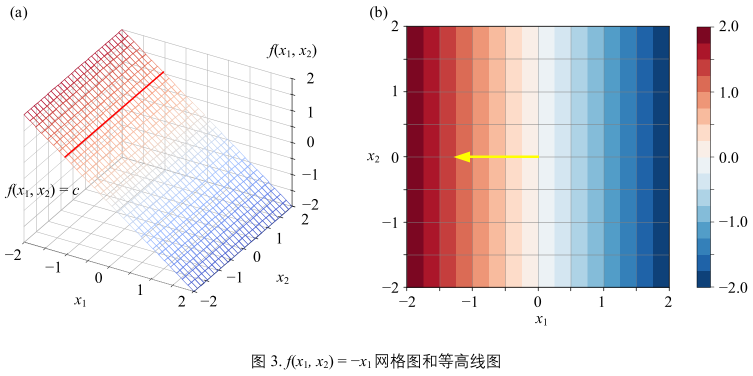
\( y = f(x_{1},x_{2}) = -x_{1} = \underbrace{\begin{bmatrix} -1\\0 \end{bmatrix}^{T}}_{\text{w}} \underbrace{\begin{bmatrix} x_{1}\\x_{2} \end{bmatrix}}_{\text{x}} \)（8）

图3（a）：

1. 平面平行于x2轴，即纵轴

图3（b)：

1. \(f(x_{1}, x_{2})\)平面等高线同样平行于x2轴
2. 黄色箭头为函数\(f(x_{1}, x_{2})\)，箭头平行x1朝左，即朝向x1轴负方向

等高线平行横轴

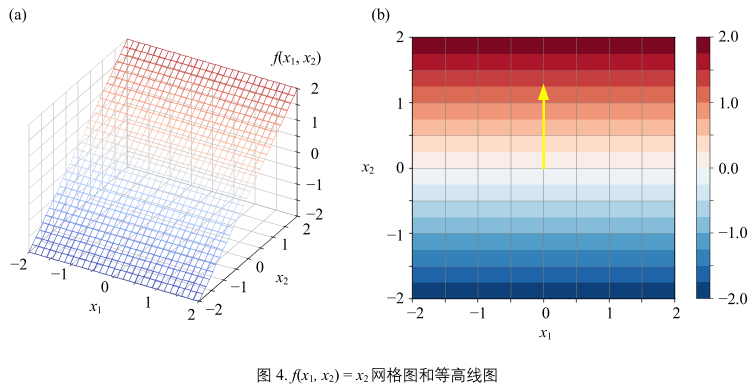
\( y = f(x_{1},x_{2}) = x_{2} = \underbrace{\begin{bmatrix} -1\\0 \end{bmatrix}^{T}}_{\text{w}} \underbrace{\begin{bmatrix} x_{1}\\x_{2} \end{bmatrix}}_{\text{x}} \)（9）

图4（a）：

1. 平面平行于x1轴

图4（b）：

1. \(f(x_{1}, x_{2})\)平面等高线同样平行于x1轴。
2. 黄色箭头同样为\(f(x_{1}, x_{2})\)增大方向，箭头指向x2轴正方向。

平面叠加

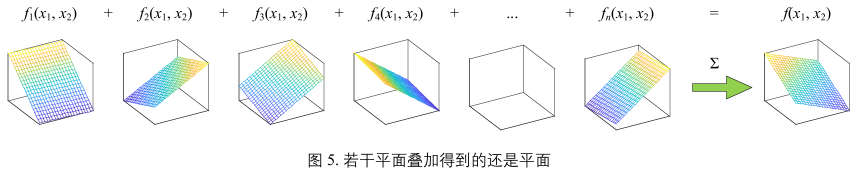
图5：
若干平面叠加得到的还是平面。函数\(f(x_{1}, x_{2})\)中下角标i为函数序号，不同序号代表不同函数。

超平面

一次函数中变量数量继续增多时，将获得超平面，解析式：
\(y = f(x_{1}, x_{2}, \dots x_{D}) = w_{1}x_{1} + w_{2}x_{2} + \dots + w_{D}x_{D} + b\) （10）

将（10）写成矩阵运算形式：
\(y = f(x) = w^{T}x + b\)
\(\boldsymbol{w} = \begin{bmatrix}w_{1} \\ w_{2} \\ \dots \\ w_{D}\end{bmatrix},\boldsymbol{x} = \begin{bmatrix}x_{1} \\ x_{2} \\ \dots \\ x_{D}\end{bmatrix}\)

表1：

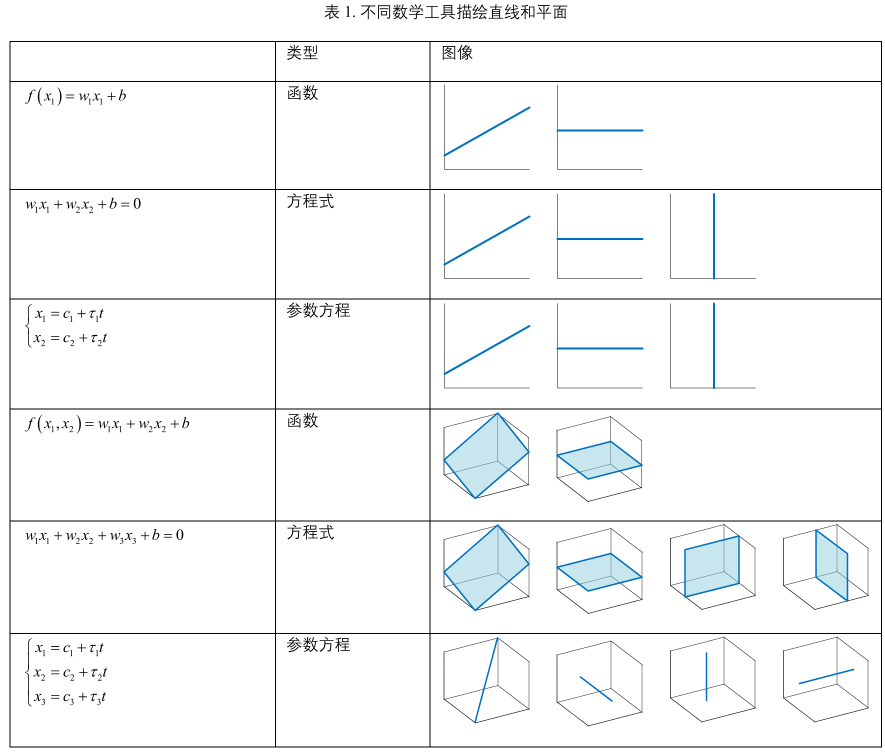
平面直线、三维空间直线、三维空间平面阔以借助不同数学工具进行描述，要格外注意区分代数中函数、方程式、参数方程三个概念之间的区别

13.2 正圆抛物面：等高线为正圆

正圆抛物面是抛物面的一种特殊形式，它的等高线为正圆。
最简单的形式：\(y = f(x_{1}, x_{2}) = a (x_{1}^{2}, x_{2}^{2})\) （13）

（13）可以写成如下矩阵运算形式：
\(y = f(x_{1}, x_{2}) = \underbrace{\begin{bmatrix} x_{1} \\ x_{2} \end{bmatrix}^{T}}_{x}\begin{bmatrix} a & 0 \\ 0 & a \end{bmatrix}\underbrace{\begin{bmatrix} x_{1} \\ x_{2} \end{bmatrix}}_{x}=a\underbrace{\begin{bmatrix} x_{1} \\ x_{2} \end{bmatrix}^{T}}_{x}\underbrace{\begin{bmatrix} x_{1} \\ x_{2} \end{bmatrix}}_{x}=ax^{T}x = a||x||^{2}\) （14）

向量的模

请格外注意（14）可以写成\(y = f(x_{1}, x_{2}) = a||x||^{2}\)这种形式，其中\(||x||\)叫向量 x 的模。

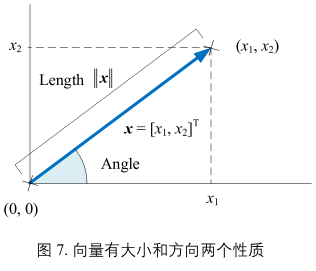
图（7）
有了坐标系，向量x可以理解为平面上有方向的线段，它有大小和方向两个性质。\(||x||\)为向量x的摸，就是向量的长度，定义：\(||x|| = \sqrt{x_{1}^{2} + x_{2}^{2}}\) （15）

观察（15），利用勾股定理，\(||x||\)相当于\((x_{1}, x_{2})\)和原点(0, 0)之间的距离，即欧氏距离。而（14）相当于欧氏距离的平方。

开口朝上

解析式：\(y = f(x_{1}, x_{2}) = x_{1}^{2} + x_{2}^{2} = \underbrace{\begin{bmatrix} x_{1} \\ x_{2} \end{bmatrix}^{T}}_{x}\begin{bmatrix} 1&0 \\ 0&1 \end{bmatrix}\underbrace{\begin{bmatrix} x_{1}\\x_{2} \end{bmatrix}}_{x}=x^{T}x = ||x||^{2}\) （16）

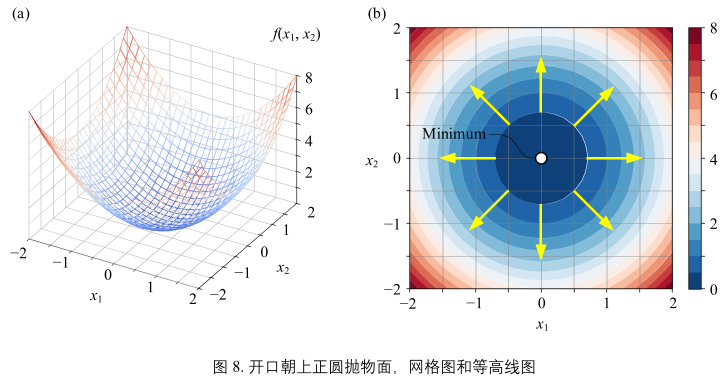
图（8）a&b：

1. 不同位置的黄色箭头都垂直于等高线，并指向函数增大方向。
2. 曲面最小值点为（0， 0）
3. 箭头发散
4. 曲面为凸面

当\(x_{1}\)为定值时，比如 \(x_{1} = 1\)，得到的曲线为抛物线：\(y = f(x_{1} = 1, x_{2}) = 1 + x_{2}^{2}\)

开口朝下

\(y = f(x_{1}, x_{2}) = -x_{1}^{2} - x_{2}^{2} = \underbrace{\begin{bmatrix} x_{1} \\ x_{2} \end{bmatrix}^{T}}_{x}\begin{bmatrix} -1&0 \\ 0&-1 \end{bmatrix}\underbrace{\begin{bmatrix} x_{1}\\x_{2} \end{bmatrix}}_{x}=-x^{T}x\) （18）

图（9）a&b：

1. 不同位置的黄色箭头都垂直于等高线，并指向函数增大方向。
2. （0， 0）处取得最大值点
3. 箭头汇聚
4. 曲面为凹面

平移

将（18）中二元函数变量\((x_{1}, x_{2})\)平移\((c_{1}, c_{2})\)
得到：\(y = f(x_{1}, x_{2}) = -(x_{1} - c_{1})^{2} - (x_{2} - c_{2})^{2} = -(x - c)^{T}(x - c) = -||x - c||^2\) 后面简称（19），其中: \(c = [c_{1}, c_{2}]^{T}\)

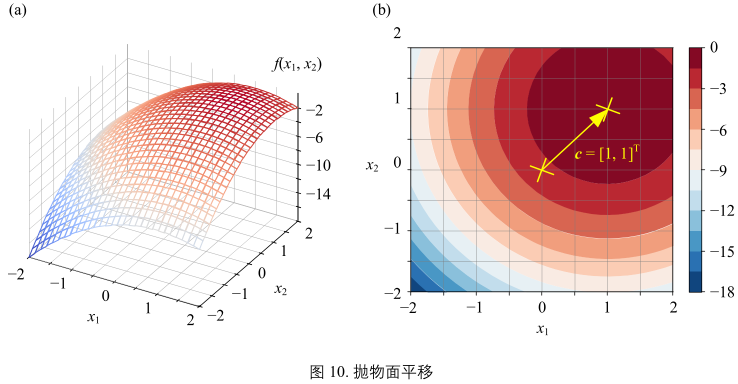
图（10）：

1. （19）对应的抛物面和等高线
2. 图（9）图像在\(x_{1}x_{2}\)平面平移\(c=[1, 1]^{T}\)得到图（10）
3. 正圆抛物面的中心移动到了\((1, 1)\)，相应的最大值也移动到了\((1, 1)\)

13.3 椭圆抛物面：等高线为椭圆

开口朝上

一般形式：
\(y = f(x_{1}, x_{2}) = \frac{x_{1}^{2}}{a^{2}} + \frac{x_{2}^{2}}{b^{2}} = \underbrace{\begin{bmatrix} x_{1} \\ x_{2} \end{bmatrix}^{T}}_{x}\begin{bmatrix} \frac{1}{a^{2}}&0 \\ 0&\frac{1}{b^{2}} \end{bmatrix}\underbrace{\begin{bmatrix} x_{1} \\ x_{2} \end{bmatrix}}_{x}\) 后面简称（20）

其中，a 和 b 都不为 0。特别地，\(a^{2} = b^{2}\) 椭圆抛物面是正圆抛物面

将（20）写成：
\(y = f(x_{1}, x_{2}) = x^{T}\begin{bmatrix} \frac{1}{a}&0 \\ 0&\frac{1}{b} \end{bmatrix}\begin{bmatrix} \frac{1}{a}&0 \\ 0&\frac{1}{b} \end{bmatrix}x = (\begin{bmatrix} \frac{1}{a}&0 \\ 0&\frac{1}{b} \end{bmatrix}x)^{T}\begin{bmatrix} \frac{1}{a}&0 \\ 0&\frac{1}{b} \end{bmatrix}x\) 后面简称（21）

图（11）：

从几何的角度来看，上式中的对角方阵起到的就是“缩放”这个几何操作。

举个例子：

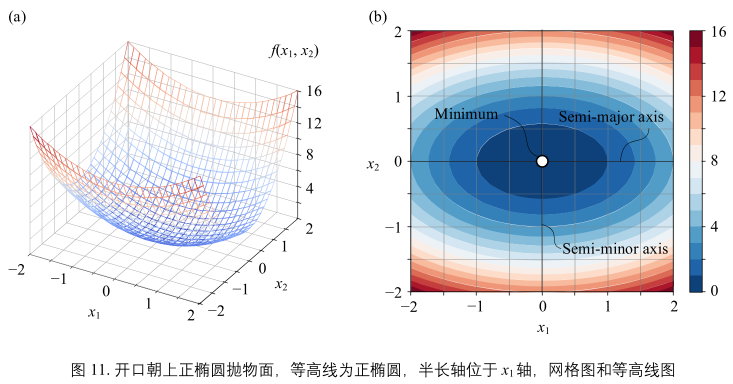
图11所示椭圆抛物面开口朝上，解析式：
\(y = f(x_{1}, x_{2}) = x_{1}^{2} + 3x_{2}^{2} = \underbrace{\begin{bmatrix} x_{1} \\ x_{2} \end{bmatrix}^{T}}_{x}\begin{bmatrix} 1&0 \\ 0&3 \end{bmatrix}\underbrace{\begin{bmatrix} x_{1} \\ x_{2} \end{bmatrix}}_{x}\)（22）

图（11）：

1. 最小值点位于（0, 0）
2. 图（8）在\(x_{2}\)轴方向以一定比例缩放得到图（11）

图（11）b：

1. 三维等高线为一系列椭圆。这些椭圆为正椭圆，其半长轴位于\(x_{1}\)轴

开口朝下

图（12）：

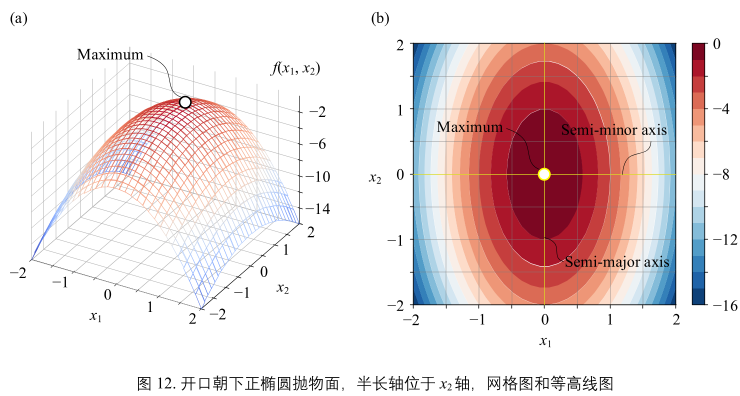
1. 最大值点位于（0, 0）
2. 半长轴位于\(x_{2}\)轴。

\(y = f(x_{1}, x_{2}) = -3x_{1}^{2} - x_{2}^{2} = \underbrace{\begin{bmatrix} x_{1} \\ x_{2} \end{bmatrix}^{T}}_{x}\begin{bmatrix} -3&0 \\ 0&-1 \end{bmatrix}\underbrace{\begin{bmatrix} x_{1} \\ x_{2} \end{bmatrix}}_{x}\)（23）

旋转

图13（a&b）：

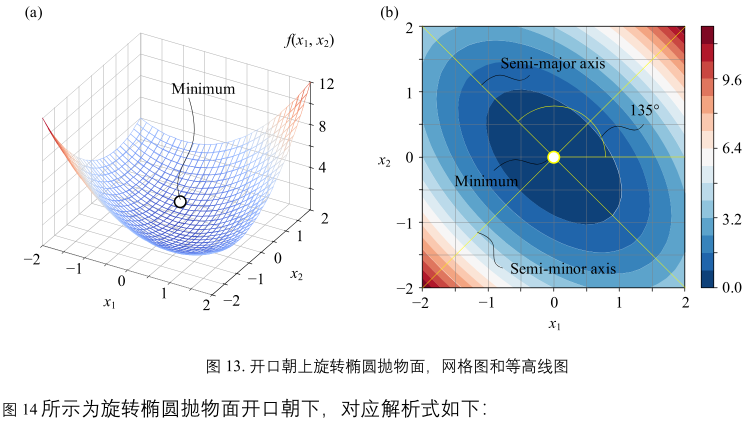
对应解析式：
\(y = f(x_{1}, x_{2}) = x_{1}^{2} + x_{1}x_{2} + x_{2}^{2} = \underbrace{\begin{bmatrix} x_{1} \\ x_{2} \end{bmatrix}^{T}}_{x}\begin{bmatrix} 1&\frac{1}{2} \\ \frac{1}{2}&1 \end{bmatrix}\underbrace{\begin{bmatrix} x_{1} \\ x_{2} \end{bmatrix}}_{x}\)（24）

图13（b）：

1. 三位等高线不再是正椭圆，而是旋转椭圆。
2. 旋转椭圆的长半轴和\(x_{1}\)轴正方向夹角135°

图14（a&b）

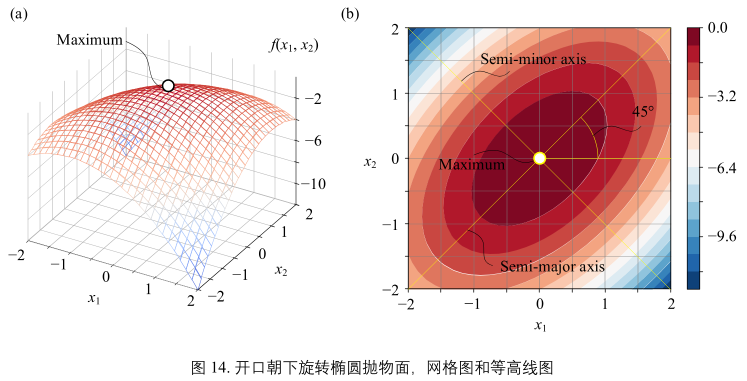
解析式：
\(y = f(x_{1}, x_{2}) = -x_{1}^{2} + x_{1}x_{2} - x_{2}^{2} = \underbrace{\begin{bmatrix} x_{1} \\ x_{2} \end{bmatrix}^{T}}_{x}\begin{bmatrix} -1&\frac{1}{2} \\ \frac{1}{2}&-1 \end{bmatrix}\underbrace{\begin{bmatrix} x_{1} \\ x_{2} \end{bmatrix}}_{x}\)（25）

1. 与图13正好相反
2. 最大值点位于（0，0）

13.4 双曲抛物面：马鞍面

双曲抛物面，也叫马鞍面，因其形状酷似马鞍而得名。
解析式：
\(y = f(x_{1}, x_{2}) = \frac{x_{1}^{2}}{a^{2}} - \frac{x_{2}^{2}}{b^{2}} \underbrace{\begin{bmatrix} x_{1} \\ x_{2} \end{bmatrix}^{T}}_{x} \begin{bmatrix} \frac{1}{a^{2}}&0 \\ 0&-\frac{1}{b^{2}} \end{bmatrix} \underbrace{\begin{bmatrix} x_{1} \\ x_{2} \end{bmatrix}}_{x} \) （26）

举个例子

图16：

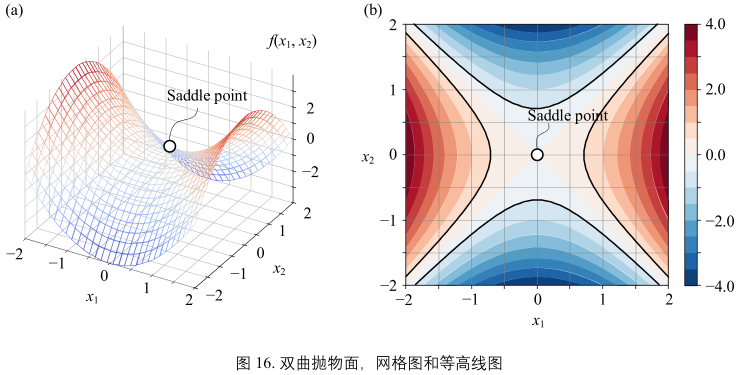
对应解析式：
\(y = f(x_{1}, x_{2}) = x_{1}^{2} - x_{2}^{2} = \underbrace{\begin{bmatrix} x_{1} \\ x_{2} \end{bmatrix}^{T}}_{x} \begin{bmatrix} 1&0 \\ 0&-1 \end{bmatrix} \underbrace{\begin{bmatrix} x_{1} \\ x_{2} \end{bmatrix}}_{x} \) （27）

观察图16（b）：

1. 三维等高线位一系列双曲线
2. 曲面中心点称作鞍点
3. 鞍点既不是曲面最大值点也不是最小值点
4. 等高线不再是闭合曲线

旋转

图17：

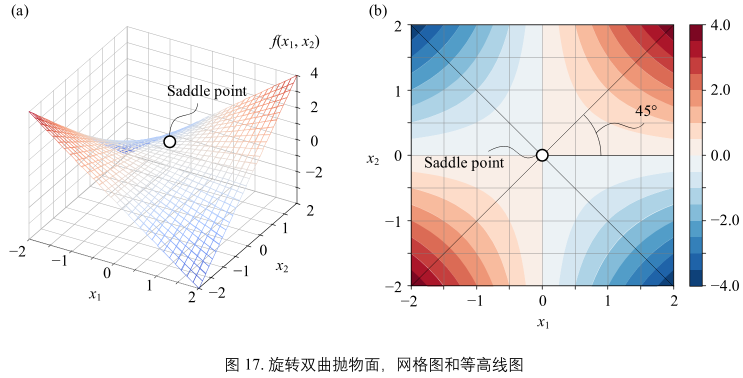
对应解析式：
\(y = f(x_{1}, x_{2}) = x_{1}x_{2} = \underbrace{\begin{bmatrix} x_{1} \\ x_{2} \end{bmatrix}^{T}}_{x} \begin{bmatrix} 0&\frac{1}{2} \\ \frac{1}{2}&0 \end{bmatrix} \underbrace{\begin{bmatrix} x_{1} \\ x_{2} \end{bmatrix}}_{x} \) （28）

观察图17（b）：

1. 等高线是一系列反比例函数
2. 是图16（b）双曲线旋转45°

13.5 山谷和山脊：无线极值点

山谷面

图18：

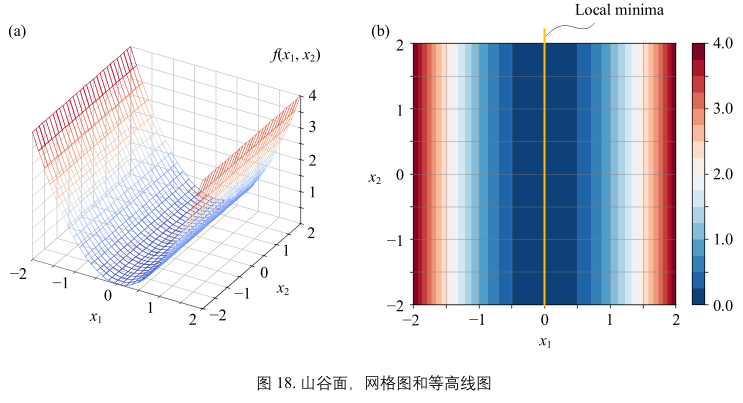
对应解析式：
\(y = f(x_{1}, x_{2}) = x_{1}^{2} = \underbrace{\begin{bmatrix} x_{1} \\ x_{2} \end{bmatrix}^{T}}_{x} \begin{bmatrix} 1&0 \\ 0&0 \end{bmatrix} \underbrace{\begin{bmatrix} x_{1} \\ x_{2} \end{bmatrix}}_{x} \) （29）

观察图18（b）：

1. 山谷面存在无数极小值
2. 这些极小值点均在一条直线上

叠加

图19：

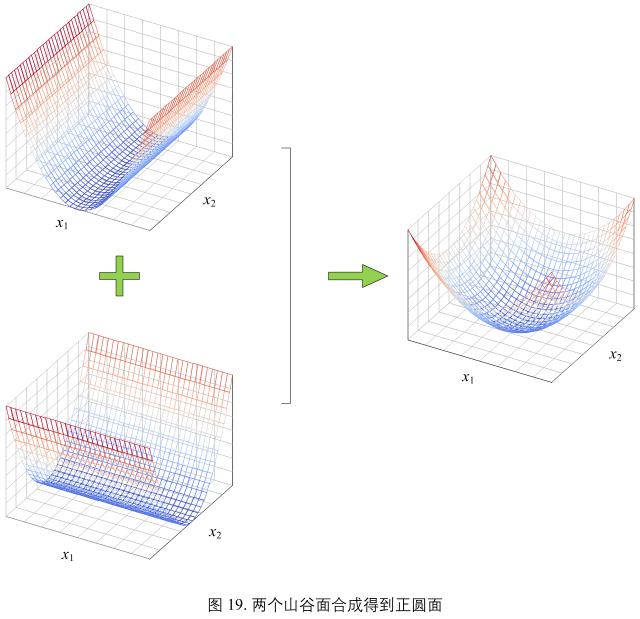
图19正圆抛物面可以看作由两个山谷面叠加得到：
\(y = f(x_{1}, x_{2}) = x_{1}^{2} + x_{2}^{2}\) （30）
很多曲面都可以看作是若干不同类型曲面叠加而成。这个几何视角对于理解一些机器学习和数据科学算法非常重要。

山脊面

图20：

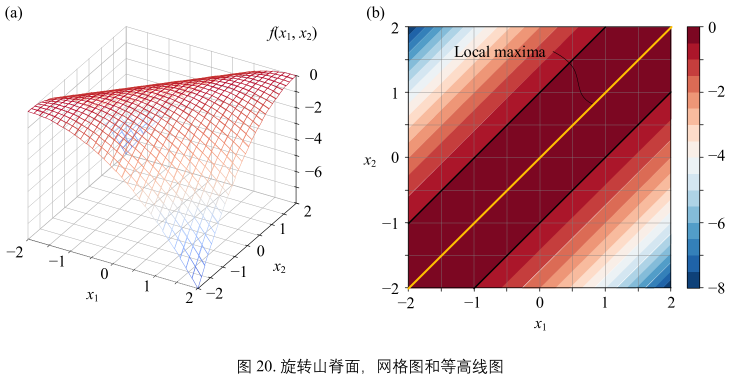
图20所示为旋转山脊面，解析式如下：
\(y = f(x_{1}, x_{2}) = \frac{x_{1}^{2}}{2} + x_{1}x_{2} - \frac{x_{2}^{2}}{2} = \underbrace{\begin{bmatrix}x_{1} \\ x_{2}\end{bmatrix}^{T}}_{x}\begin{bmatrix}-\frac{1}{2} & \frac{1}{2} \\\frac{1}{2} & -\frac{1}{2}\end{bmatrix}\underbrace{\begin{bmatrix}x_{1} \\ x_{2}\end{bmatrix}}_{x}\) （31）

图20（b）：

1. 山脊面有一系列极大值点，它们在同一条斜线上
2. 黑色等高线不同点绘制梯度方向箭头

13.6 锥面：正圆抛物面开方

开口朝上

开口朝上正圆抛物面解析式开平方取正，便得到锥面。

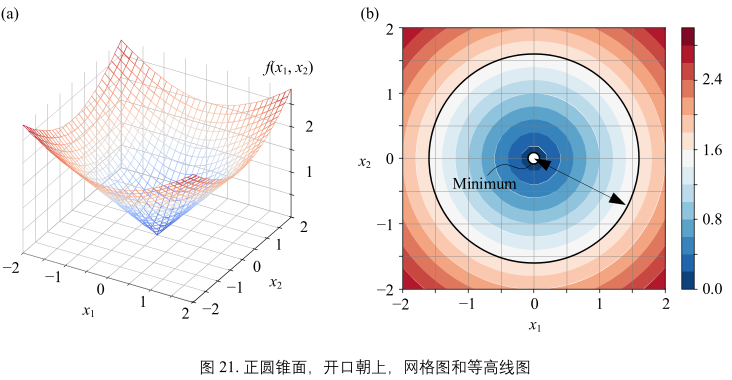
图21所示锥面开口向上解析式：
\(y = f(x_{1}, x_{2}) = \sqrt{x_{1}^{2} + x_{2}^{2}} = \sqrt{\boldsymbol{x^{T}} + \boldsymbol{x}} = ||\boldsymbol{x}||\) （33）

观察图21（b）：

1. 锥面的等高线为一系列同心圆
2. （0，0）处取最小值
3. （0，0）并不光滑，该点为尖点
4. 不同等高线之间均匀渐变
5. 不同等高线代表和（0，0）距离相同，这些等高线就是欧式距离“等距线”

开口朝下

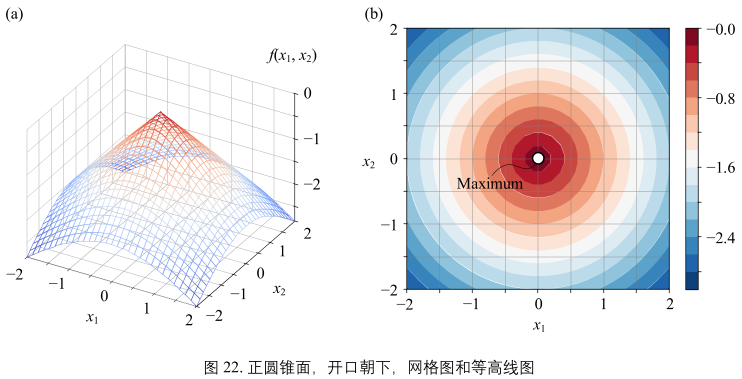
（33）解析式加上负号便得到了图22开口向下锥面：
\(y = f(x_{1}, x_{2}) =-\sqrt{x_{1}^{2} + x_{2}^{2}} = \sqrt{\boldsymbol{x^{T}} + \boldsymbol{x}} = ||\boldsymbol{x}||\)

对顶圆锥

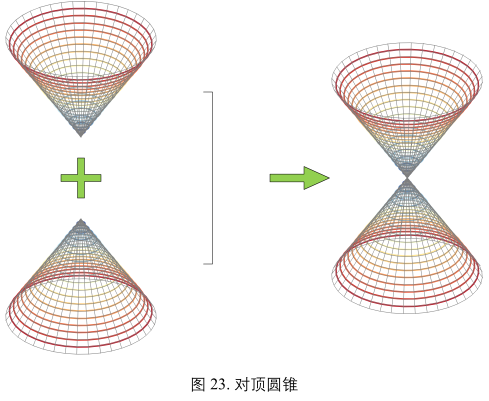
中轴保持在一条直线撒谎给你，将图21和图22两个圆锥面在顶点处拼接在一起获得对顶圆锥

13.7 绝对值函数：和超椭圆有关

平面对折

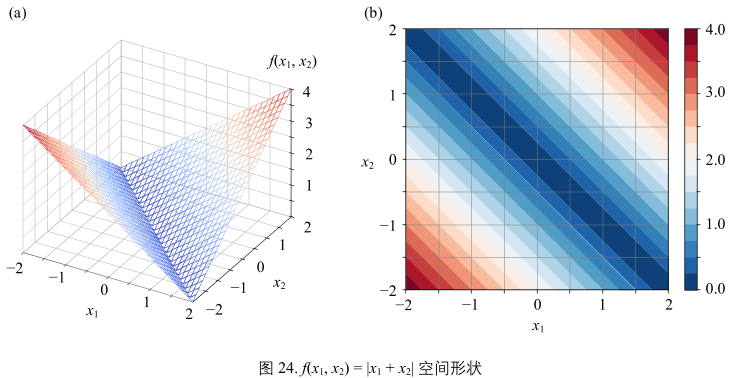
第一个例子：
\(x_{1} + x_{2}\) 取绝对值
解析式：\(y = f(x_{1}, x_{2}) = |x_{1} + x_{2}|\) （35）

此外（35）相当于旋转山谷面解析式开平方取正：
\(y = f(x_{1}, x_{2}) = \sqrt{(x_{1} + x_{2})^{2}}\)（36）

旋转正方形

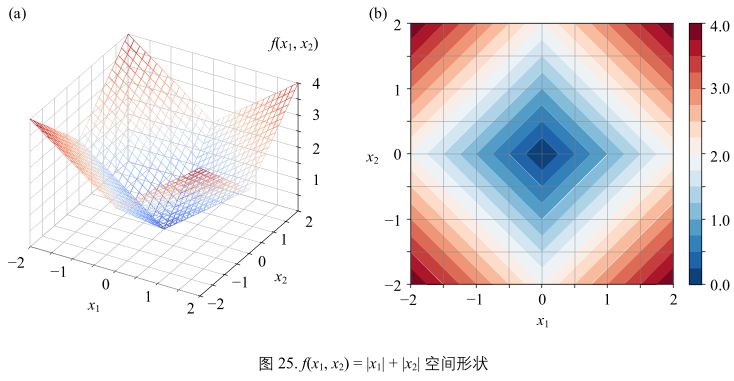
第二个例子：
\(x_{1}\) \(x_{2}\)分别取绝对值
\(y = f(x_{1}, x_{2}) = |x_{1}| + |x_{2}|\) （37）

正方形

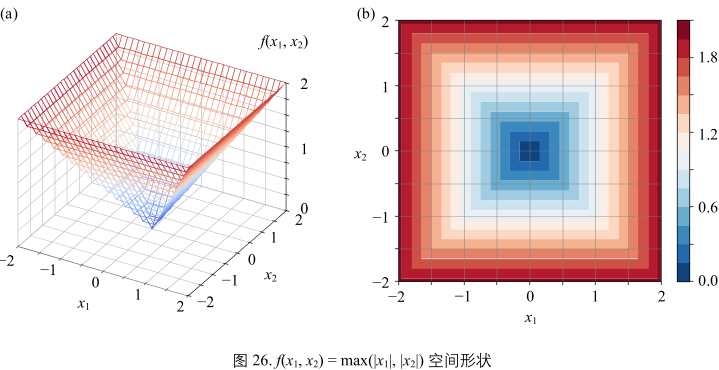
第三个例子：
x1 x2 分别取绝对值，比大小后，取两者中最大值
\(y = f(x_{1}, x_{2}) = max(|x_{1}|, |x_{2}|)\)（38）

13.8 逻辑函数：从一元到二元

二元逻辑函数解析式：
\(y = f(x_{1}, x_{2}) = \frac{1}{1 + exp(-(w_{1}x_{1} + w_{2}x_{2} + b))}\)（40）

写成矩阵运算形式：
\(y = f(x_{1}, x_{2}) = \frac{1}{1 + exp(-(\boldsymbol{w}^{T} + \boldsymbol{x} + b))}\)（41）
（41）可以看作一个符合函数

举个例子

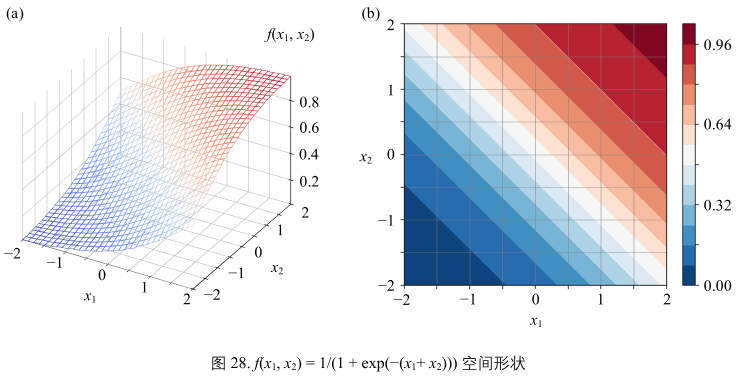
当w1 = 1, w2 = 1, b = 0时，（40）可以写成：
\(y = f(x_{1}, x_{2}) = \frac{1}{1 + exp(-(x_{1} + x_{2}))}\)（42）

图28：

1. x1 + x2 趋近正无穷时，（42）却无法达到1.
2. x1 + x2 趋近负无穷时，（42）却无法达到0.

再举个例子

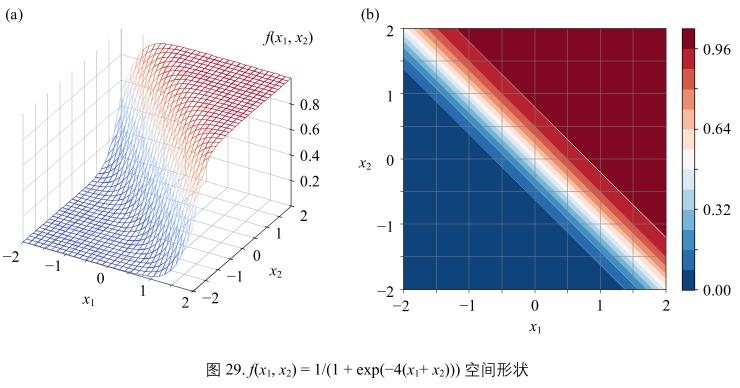
当w1 = 4, w2 = 4, b = 0时，（40）可以写成：
\(y = f(x_{1}, x_{2}) = \frac{1}{1 + exp(-4(x_{1} + x_{2}))}\)（43）

图29：
当w1和w2增大后，破面变得陡峭

二元 tanh() 函数

逻辑函数是S型函数的一种；机器学习中，sigmoid函数很多时候特指tanh()函数，解析式：
\(y = f(x_{1}, x_{2}) = tanh(\gamma(w_{1}x_{1} + w_{2}x_{2}) + r)\)（44）

写成矩阵形式：
\(y = f(\boldsymbol{x}) = tanh(\gamma\boldsymbol{w}^{T}\boldsymbol{x} + r)\)（45）

举个例子

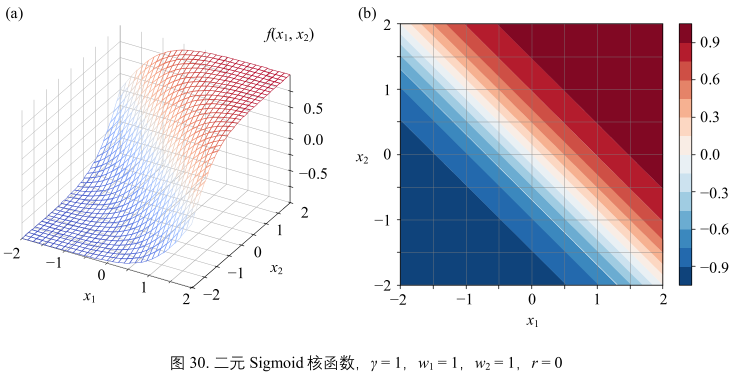
y = 1, w1 = 1, w2 = 1, r = 0时，可以写成：
\(y = f(x_{1}, x_{2}) = tanh(x_{1} + x_{2})\)（46）

图30：

1. 当 \(\gamma\) 增大时，曲面也变得陡峭。

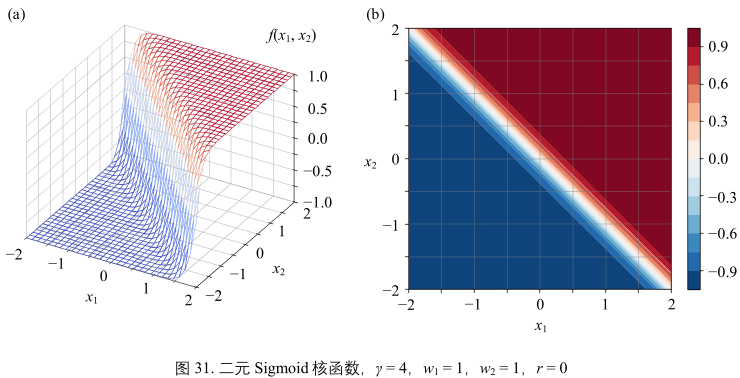
图31是 y = 4, w1 = 1, w2 = 1, r = 0时的图像

13.9 高斯函数：机器学习的多面手

二元高斯函数的一般形式：
\(y = f(x_{1}, x_{2}) = exp(-\gamma((x_{1} - c_{1})^{2} + (x_{2} - c_{2})^{2}))\)（47）

举个例子

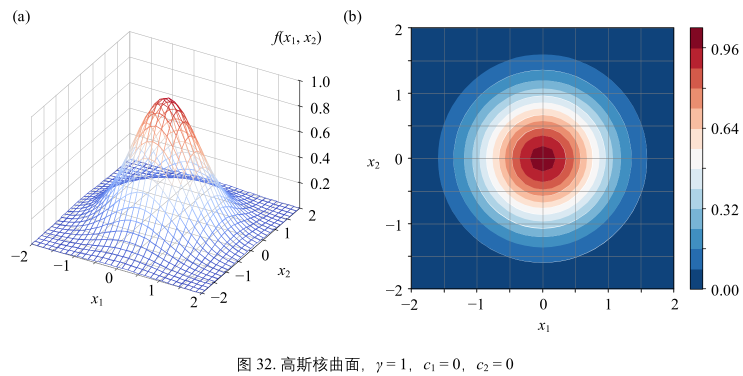
\(\gamma\) = 1, c1 = 0, c2 = 0时，二元高斯函数的解析式：
\(y = f(x_{1}, x_{2}) = exp(-(x_{1}^{2} + x_{2}^{2})) = exp(-\boldsymbol{x}^{T}\boldsymbol{x}) = exp(-||x||^{2})\)（48）

再举个例子

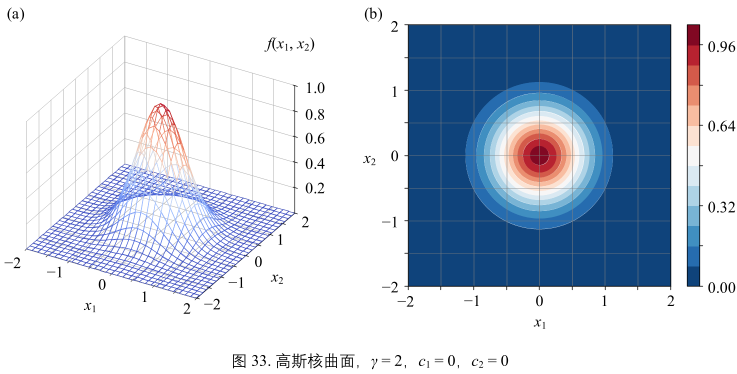
\(\gamma\) = 2, c1 = 0, c2 = 0时，二元高斯函数的解析式：
\(y = f(x_{1}, x_{2}) = exp(-2(x_{1}^{2} + x_{2}^{2})) = exp(-2\boldsymbol{x}^{T}\boldsymbol{x}) = exp(-2||x||^{2})\)（49）
比较图32和图33，可以发现随着 \(\gamma\) 增大，曲面边得更尖，更陡峭。

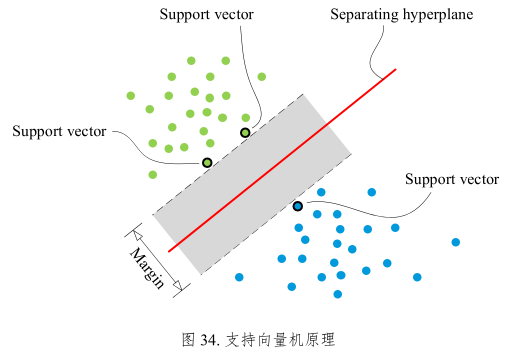
图34：
支持向量机 SVM 基本原理就是找到一条灰色“宽带”，将绿色和蓝色点分开，并让灰色“间隔”最宽。灰色“间隔”中心线（图34中红色直线）便是分割衔接，即分类决策边界。

图35：
实际情况很多数据不能用一条直线将不同标签样本分类。对于这种情况，我们需要采用核技巧。核技巧的基本思路就是将数据映射到高维空间中，让数据在这个高维空间中线性可分。

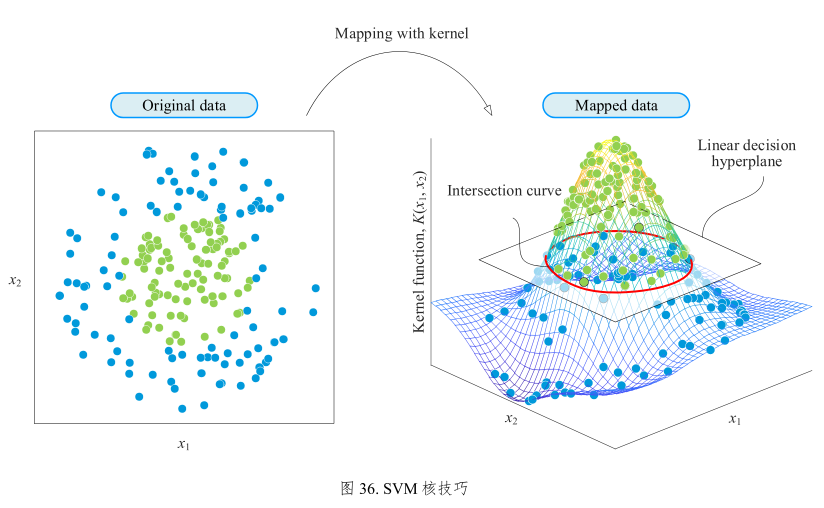
图36：
原数据线性不可分，显然不能用一条直线将数据分成两类。但是将原来的二维数据映射到三维空间之后，就可以用一个平面将数据轻易分类。这个投射规则便是核函数，而高斯函数是最重要的核函数之一。右图由若干高斯函数叠加而成。红色等高线便是分类决策边界。

注：以上内容均摘自生姜博士的鸢尾花书系列-Book_3《数学要素》