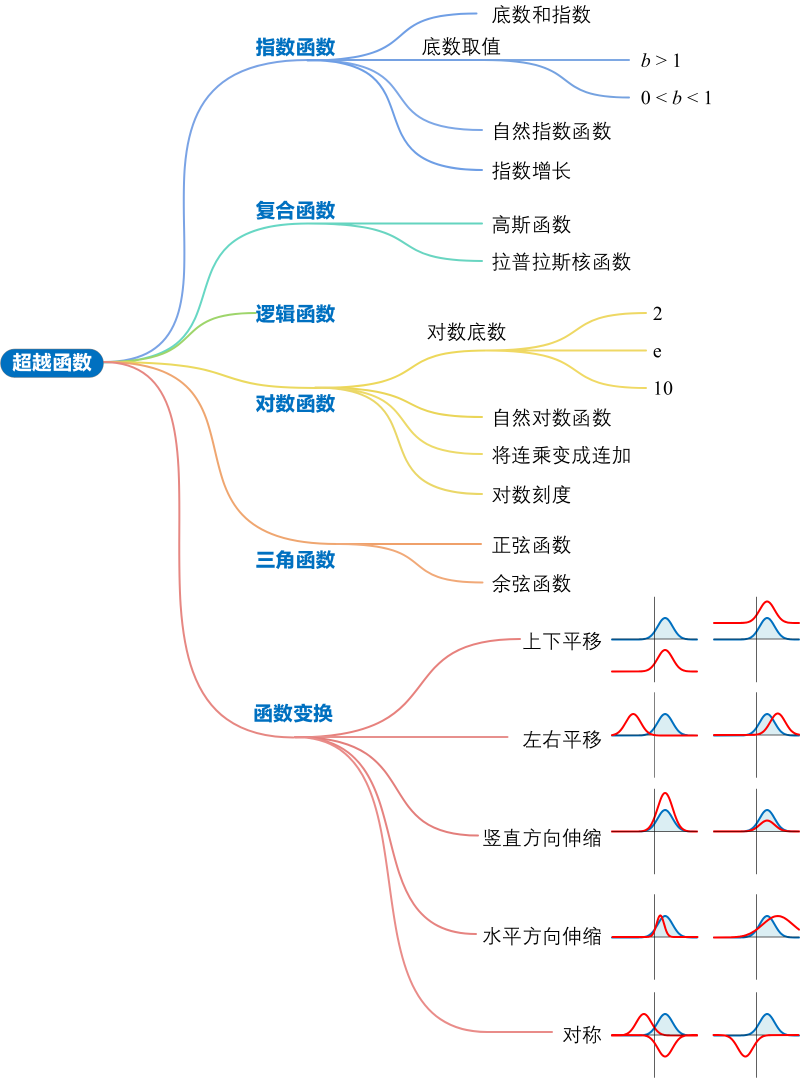
鸢尾花书 - Book_3《数学要素》 - Chapter12 超越函数
12.1 指数函数:指数为自变量
指数函数一般形式:\(f(x) = b^{x}\)
注:幂函数的自变量为底数,而指数函数的自变量为指数
图1:
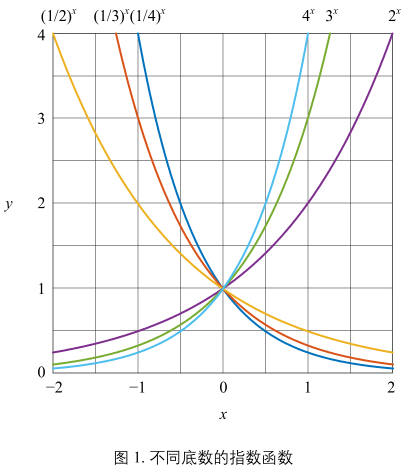
当底数取不同值时指数函数的图像,这几条曲线都经过(0,1)
区分底数 b > 1 和 0 < b < 1 两种情况对应的指数函数图像。
b > 1:\(f(x) = b^{x}\) 单调增
0 < b < 1: \(f(x) = b^{x}\) 单调减
自然指数函数
更多情况下指数函数指的是自然指数函数:\(f(x) = e^{x} = exp(x)\)
自然指数函数中的“自然”指的是自然常数 e 为底数 \(e \cong 2.718\)
可以将自然指数函数转换以 e 为底数的函数:
\(y = f(x) = b^{x} = e^{lnbx} = exp(lnbx)\)
指数增长
指数增长模型:\(G(t) = (1 + r)^{t}\)
r 为年化增长率,t为年限
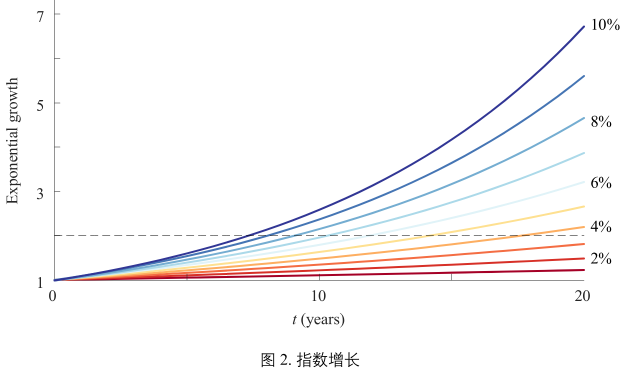
图2:
当增长率 r 取不同值时,指数增长模型G(t)和年限对应的关系。
翻倍时间指增长翻倍所用的时间。
横轴的虚线就是增长翻倍所对应的高度
12.2 对数函数:把连乘变成连加
对数函数解析式:\(y = f(x) = log_{b}(x)\)
其中 b 为对数底数,b > 0 且 b != 1。上述对数函数的定义域为 x > 0
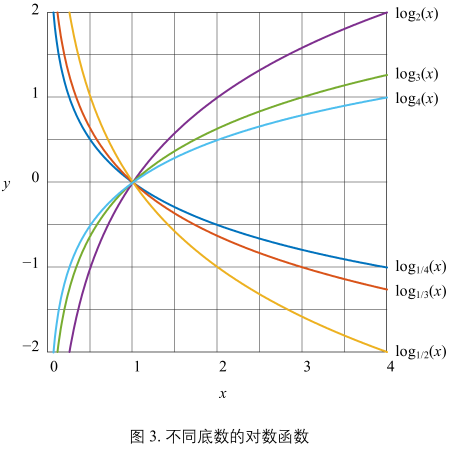
图3:
b > 1 时,单调增
0 < b < 1 时,单调减
自然对数函数
\(y = f(x) = ln(x) = log_{e}(x)\)
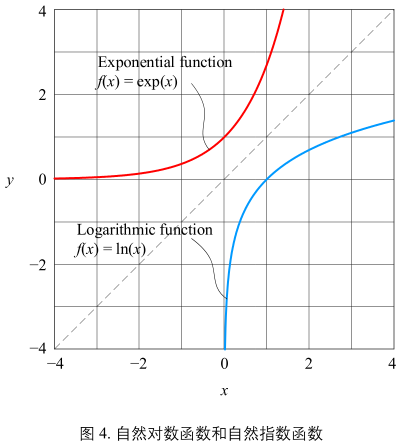
图4:
自然指数函数(红色)和自然对数函数(蓝色)互为反函数,两条曲线关于图中画线对称
对数运算特点
\(log_{b}x = \frac{log_{k}x}{log_{k}b}\)
\(log_{b}x = \frac{log_{10}x}{log_{10}b} = \frac{lnx}{lnb}\)
\(log_{b^{n}}x^{m} = \frac{m}{n}log_{b}x\), \(x = b^{log_{b}(x)}\), \(x^{log_{b}(y)} = y^{log_{b^{(x)}}}\)
对数的一个重要的性质是,把连乘变成连加:
\(log_{b}(xyz) = log_{b}x + log_{b}y + log_{b}z\)
- 用对数运算把连乘变成连加,是因为连乘不容易求偏导,连家更容易求偏导。
- 高斯函数存在 exp() 项,ln()可以把指数项变成求和形式,再者ln()不改变单调性。
对数刻度
对数刻度是一种非线性刻度,常用来描述较大的数值。
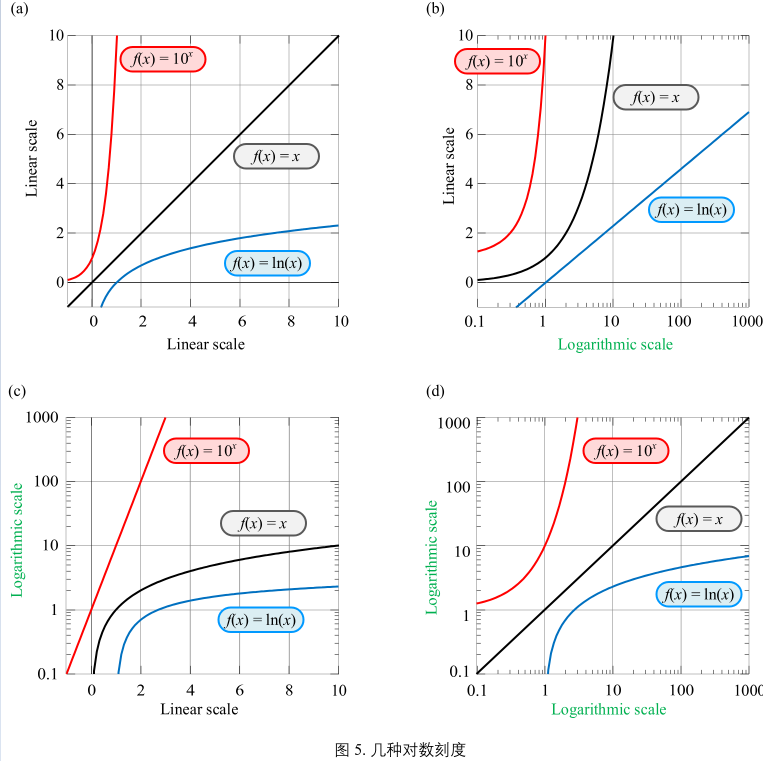
图5(a):
横轴和纵轴都是线性刻度,图中一元一次函数 \(f(x) = x\) 为一条直线。
图5(b):
横轴为对数刻度,图中对数函数 \(f(x) = ln(x)\) 为一条直线。
图5(c):
纵轴为对数刻度,其中指数函数 \(f(x) = 10^{x}\) 为一条直线。
图6(d):
横纵都是对数刻度,图中一元一次函数 \(f(x) = x\) 还是一条直线。
12.3 高斯函数:高斯分布之基础
高斯函数
自然指数函数复合二次函数,得到高斯函数:\(f(x) = exp(-\gamma x^{2})\)
其中 \(\gamma\) 为参数,\(\gamma > 0\)。
定义域 \((-\infty, +\infty)\)
值域:(0, 1]
\(f(x) = exp(-\gamma x^{2})\) 关于 x = 0 对称
高斯函数无限接近0,却不到达0
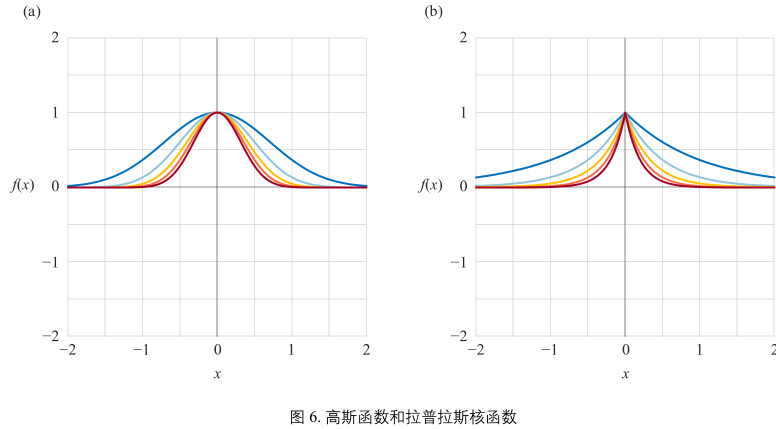
图6(a)
\(\gamma\) 决定高斯函数的形状
最基本的高斯函数:
-
\(f(x) = exp(-x^{2})\)
通过缩放、平移等变换可以得到下面的公式。 -
\(f(x) = a \cdot exp(\frac{-(x-b)^{2}}{2c^{2}})\) 关于 x = b 对称
高斯函数和高斯分布(Gaussian distribution)的概率密度函数(Probability Density Function, PDF)直接相关。高斯函数可以进一步推广得到径向基核函数(radial basis function, RBF)
拉普拉斯核核算
\(f(x) = exp(-\gamma|x|)\)
图6(b)
\(\gamma\) 决定拉普拉斯核函数的形状
x = 0 处有“尖点”,它破坏了函数的平滑。拉普拉斯核函数也经常出现再机器学习一些算法中。
12.4 逻辑函数:在 0 和 1 之间取值
逻辑函数也可以视作是自然指数函数扩展得到的复合函数
最简单的一元逻辑函数:\(f(x) = \frac{1}{1+exp(-x)} = \frac{exp(x)}{1+exp(x)}\)
更一般的一元逻辑函数形式为:\(f(x) = \frac{1}{1+exp(-(b_{0}+b_{1}x))}\)
图8:
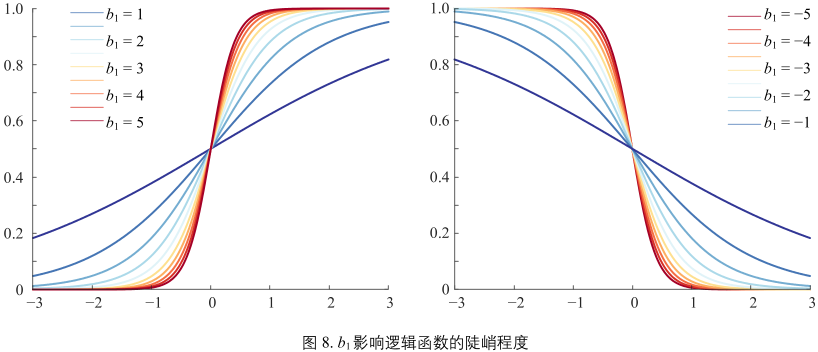
逻辑函数取值范围在 0 和 1 之间,函数无限接近 0 和 1,却不能达到。
\(b_{1}\) 影响图像的陡峭程度,注意图 \(b_{0} = 0\)
中心点位置
确定 \(f(x) = \frac{1}{2}\) 位置:
\(f(x) = \frac{1}{1+exp(-(b_{0}+b_{1}x))} = \frac{1}{2}\)
整理得到:
\(x = \frac{b_{0}}{b_{1}}\)
这个点被称作为逻辑函数中心所在位置。
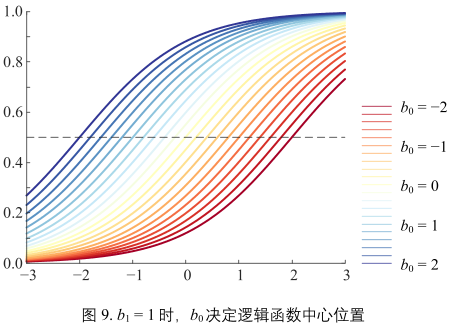
图9:
\(b_{1} = 1\),\(b_{0}\) 决定逻辑函数中心所在位置
逻辑斯谛增长
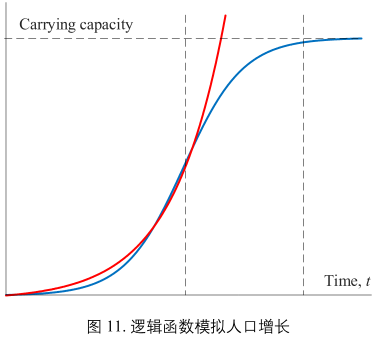
图11:
J 型增长:指数增长,一般只在一段时间内存在。各种条件会限制增长幅度,比如人口增长不可能一直按照指数增长持续下去,毕竟地球的承载能力有限。
S 型增长:开始阶段类似指数增长。然后由于各种因素,增长阻力增大,增速开始放慢。最后增长逐渐停止,趋向于瓶颈。
S 型函数
常见的S型函数还有:
- 双曲正切函数\(f(x) = tanh(x)\)
- 反正切函数\(f(x) = arctan(x)\)
- 误差函数\(f(x) = erf(x)\)
等等......
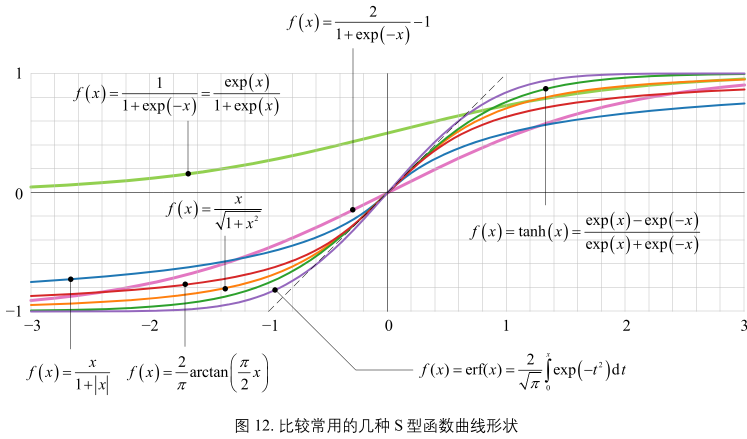
图12:
列出了比较常见的 S 型函数曲线。
tanh() 函数
在很多机器学习算法中,sigmoid 函数特指 tanh() 函数。
tanh() 函数一般式:\(f(x) = tanh(\gamma x)\)
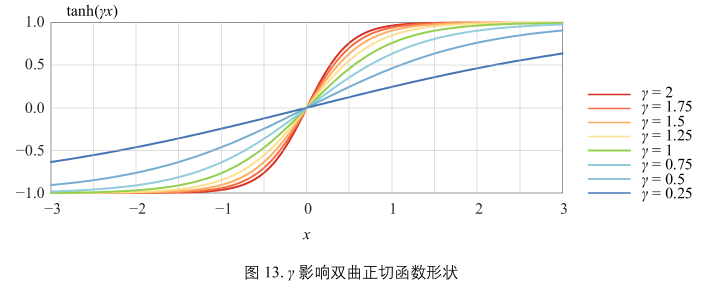
图13:
\(\gamma\) 如何影响曲线形状
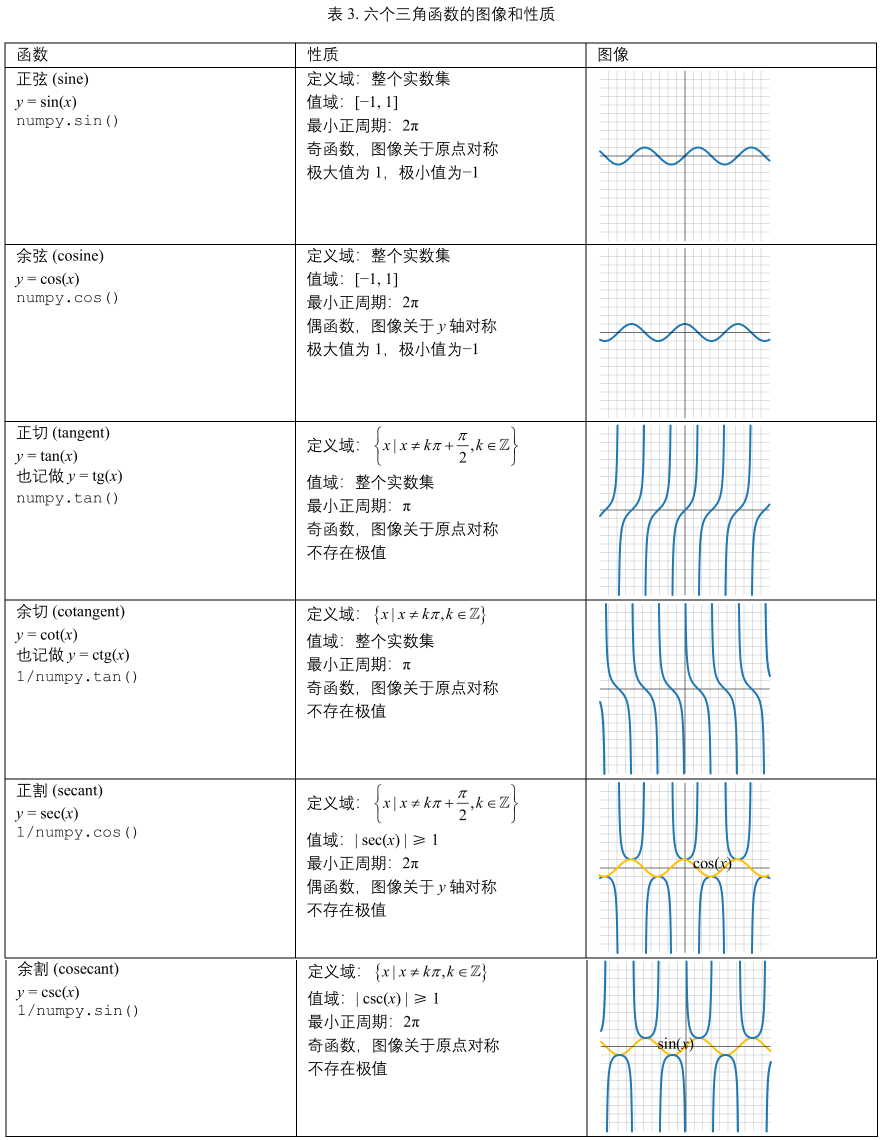
12.5 三角函数:周期函数的代表
正弦函数
\(y = f(x) = sin(x)\)
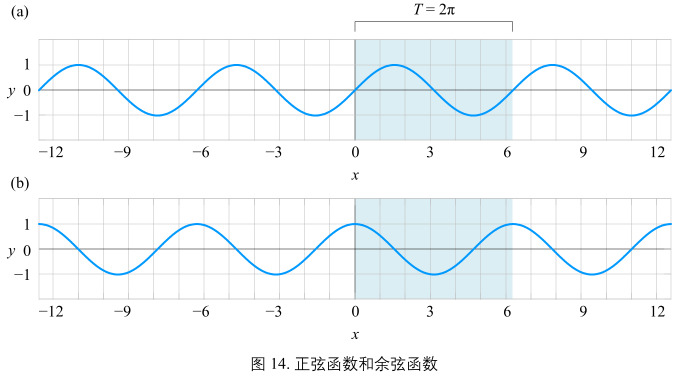
图14(a):
- 奇函数
- 关于原点对称
- 函数周期\(T = 2 \pi\)
- 值域 [-1, 1]
- 取得极大值1对应的x为:\(x = \frac{\pi}{2} + 2 \pi n\),n为整数
- 取得极小值-1对应的x为:\(x = -\frac{\pi}{2} + 2 \pi n\)
余弦函数
\(y = f(x) = cos(x)\)
- 偶函数
- 关于纵轴对称 (相当于 \(sin(x) 水平向左移动 \frac{\pi}{2}\))
- 函数周期\(T = 2 \pi\)
- 值域 [-1, 1]
12.6 函数变化:平移、缩放、对称
利用高斯函数探讨函数变换。常见函数变换有三种:
- 平移
- 缩放
- 对称
给定某个函数 y = f(x) 解析式:\(f(x) = 2exp(-(x-1)^{2})\)
平移
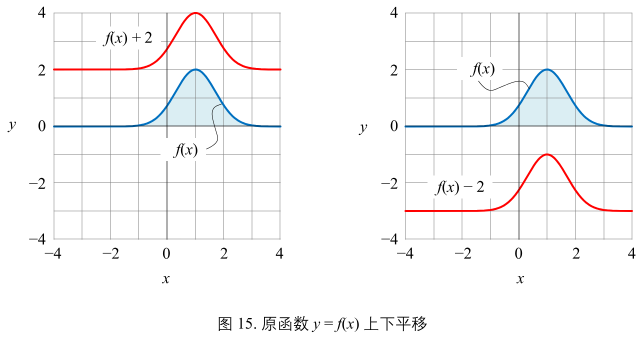
图15:
相对 y = f(x)
- f(x) + c 竖直向上平移 c 单位;
- f(x) - c 竖直向下平移 c 单位;
图16:
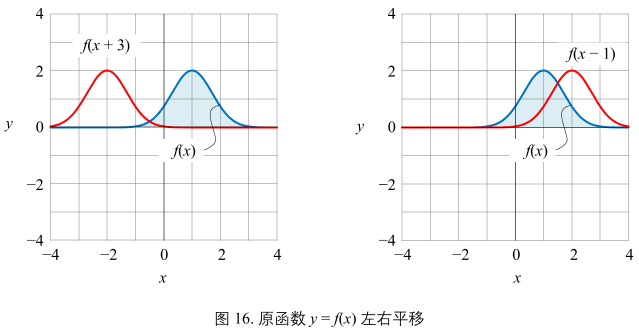
相对 y = f(x)
- f(x + c) 向左平移 c 单位;
- f(x - c)向右平移 c 单位;
水平平移不影响函数图像和横走包围的面积
缩放
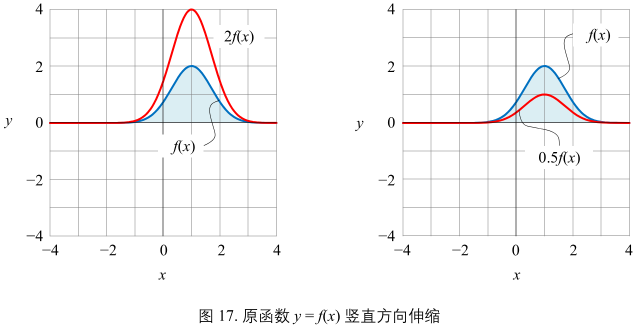
图17:
相对 y = f(x)
- cf(x) 竖直方向伸缩;
c > 1 时,cf(x) 竖直方向拉伸;
0 < c < 1 时,竖直方向压缩;
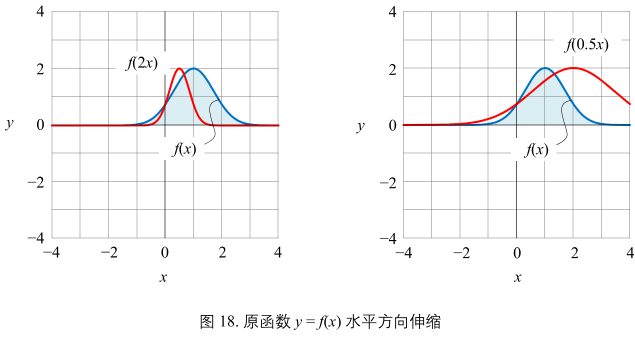
图18:
相对 y = f(x)
f(cx) 水平方向伸缩
c > 1 时,水平方向压缩;
0 < c < 1 时,水平方向拉伸;
面积等比例缩放,缩放比例为 1/c

图19:
相对 y = f(x)
cf(cx) 面积不变
对称
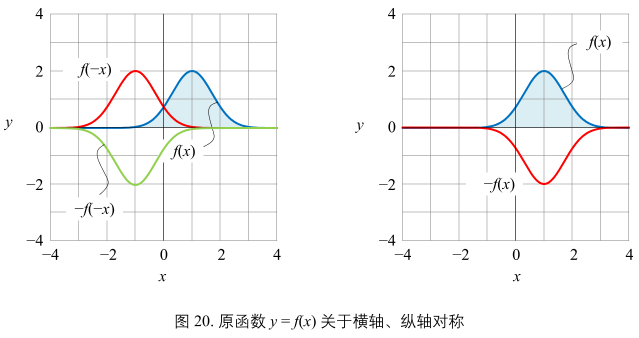
图20:
相对 y = f(x)
f(-x) 相当于函数关于 y 轴对称
-f(x) 相当于函数关于 x 轴对称
f(x) 和 -f(-x) 关于原点对称
一元高斯分布的概率密度函数解析式如下:
\(p(x) = \frac{1}{\sqrt[\sigma]{2\pi}}exp(\frac{-1}{2} (\frac{x - \mu}{\sigma})^{2})\) 后面简称 (26)
\(\mu\) 为均值,\(sigma\) 为标准差
观察(26)中指数部分存在两个函数变换:
- 横轴缩放 \(\sigma\)
- 横轴平移 \(\mu\)
令 \(z = \frac{x - \mu}{\sigma}\) 后面简称(27)
将(27)带入(26),整理得到:
\(f(x) = \frac{1}{\sqrt[\sigma]{2\pi}}exp(\frac{-1}{2}z^{2})\) 后面简称(28)
(28)中分母 \(\sqrt[\sigma]{2\pi}\),起到的是纵向缩放的作用,保证曲线下方面积为1
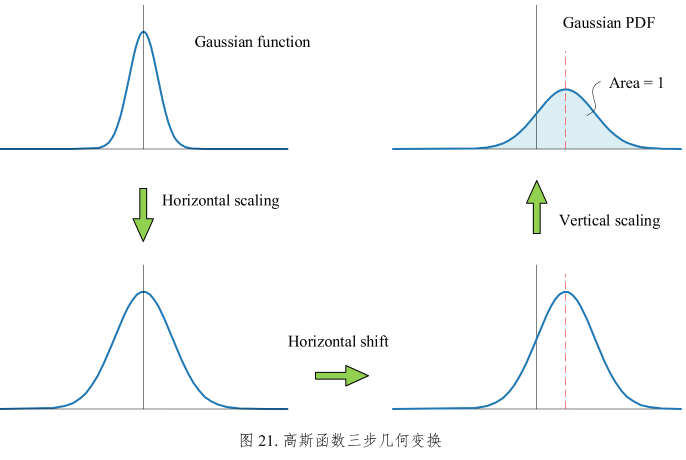
图21:
(26)(27)(28) 变换
注:以上内容均摘自生姜博士的鸢尾花书系列-Book_3《数学要素》




 浙公网安备 33010602011771号
浙公网安备 33010602011771号