鸢尾花书 - Book_3《数学要素》 - Chapter11 代数函数

11.2 一次函数：一条斜线

图3（a）：斜截式

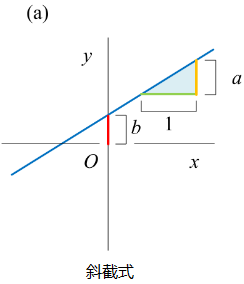
\(y = f(x) = ax + b\)
两个参数：斜率 a 和 y 轴截距 b，对于一次函数，斜率 a 不能为 0
当 a = 0，函数为常函数，即水平线
当 b = 0，函数为比例函数

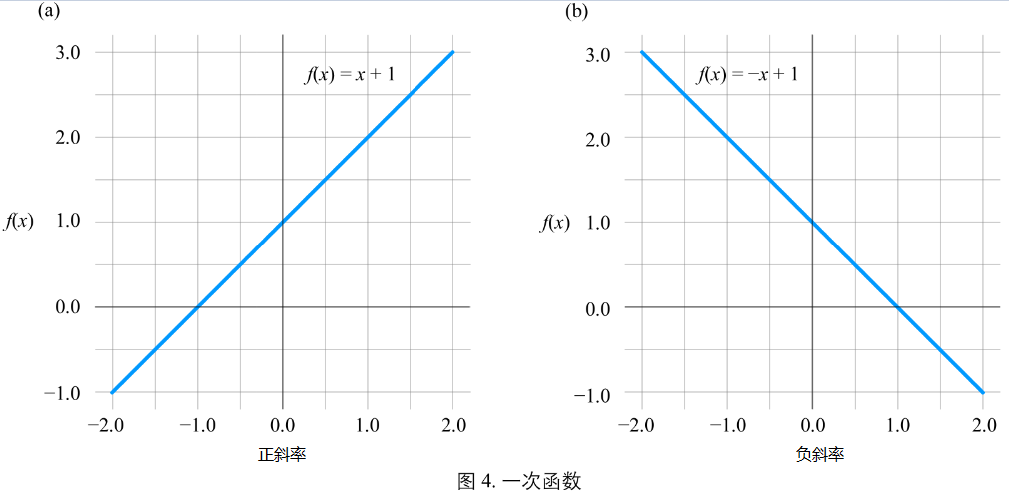
图4（a）：正斜率，斜率大于0，单调增。

图4（b）：负斜率，斜率小于0，单调减。

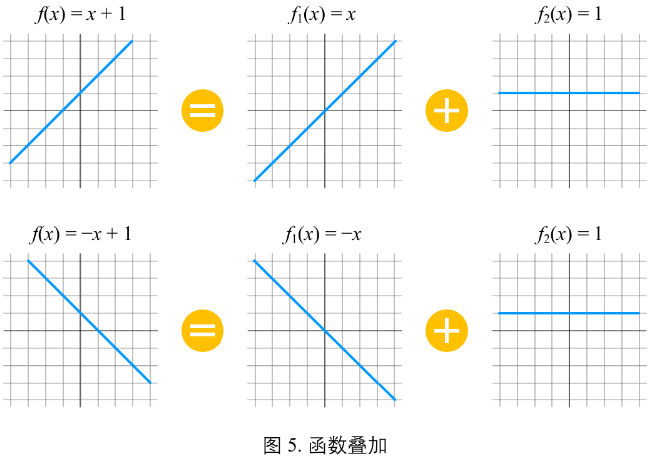
简单函数叠加和符合可以得到更复杂的函数

斜率

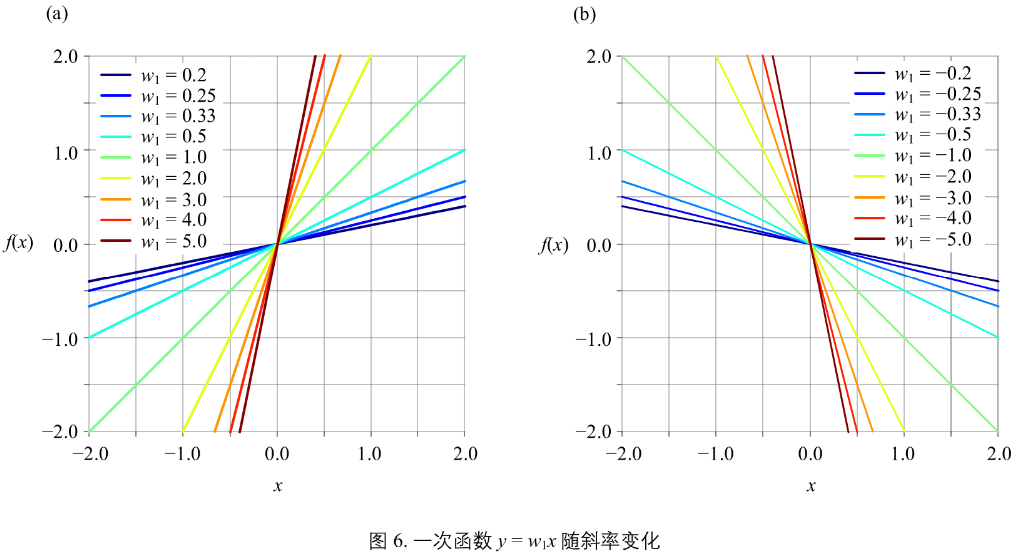
图6：
一次函数 \(y = w_{1}x\) 随斜率变化，\(w_{1}\) 的绝对值越大，一次函数图像越陡峭

截距

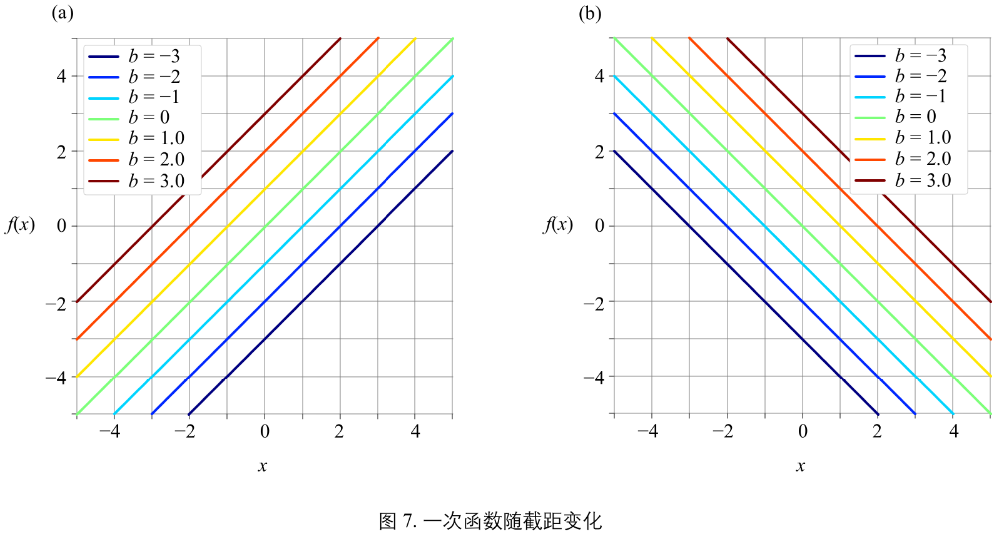
图7：
一次函数随 y 轴截距变化情况。调整一次函数函数 y 轴截距大小，相当于图像上下平移。

两条直线关系

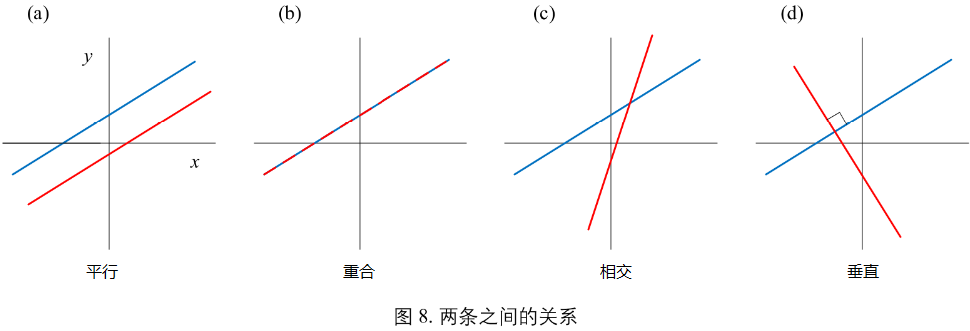
图3（b）：点斜式

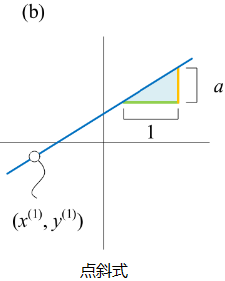
\(y - y^{(1)} = f(x) - y^{(1)} = a(x - x^{(1)})\)
给定斜率 a 和直线上的一个点 \((x^{(1)}, y^{(1)})\)，便可以确定平面上一条直线。

图3（c）：两点式

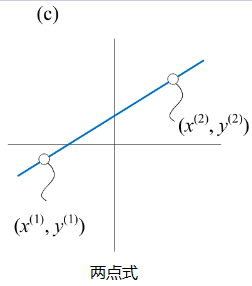
$ y - y_{(1)} = \underbrace{\frac{y^{(2)} - y^{(1)}}{x - x^{(1)}}}_{\text{Slope}}(x - x^{(1)})$

其中 \(x^{(1)} \ne x^{(2)}\)

两点式展开：\((y - y^{(1)})(x^{(2)} - x^{(1)}) = (y^{2} - y^{(1)})(x - x^{(1)})\)

图3（d）：参数方程

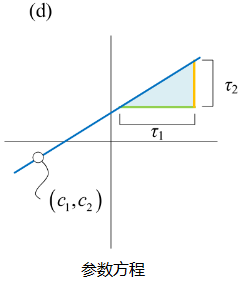
11.3 二次函数：一条抛物线

三种形式

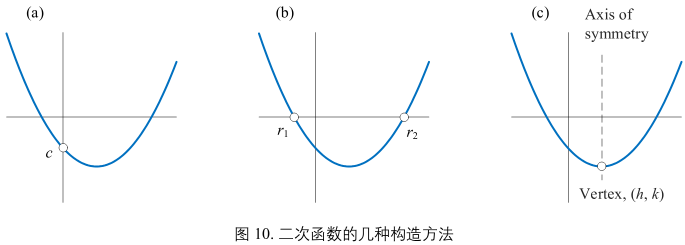
1. 基本式，图（a）
   二次函数的基本形式：\(f(x) = ax^{2} + bx + c, a \ne 0\)
   a：二次项系数，不为 0
   b：一次项系数
   c：常数项，也叫 y 轴截距

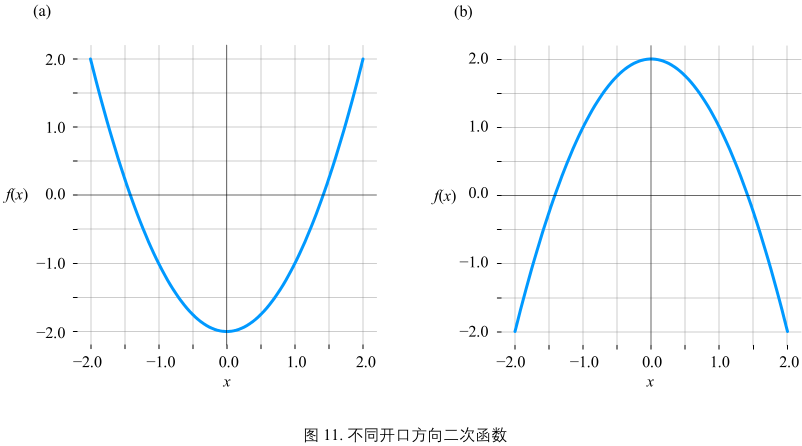
图11（a）：
开口向上，顶点位于 y 轴，顶点位置对应函数最小值，凸函数。

图12（b）：
开口向下，顶点位于 y 轴，顶点位置对应函数最大值，凹函数。

开口大小

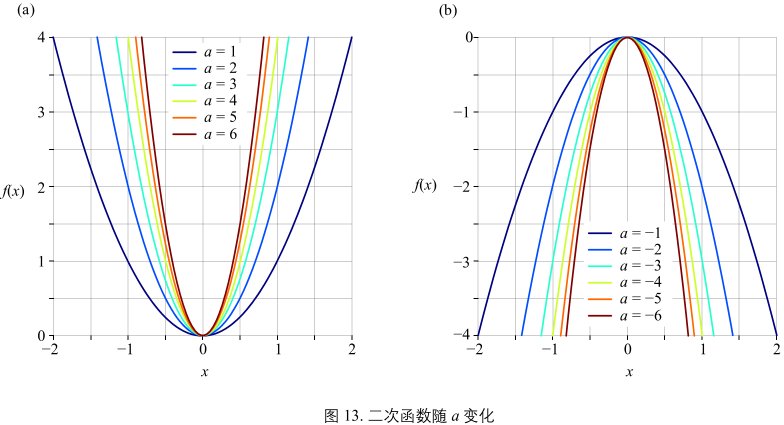
图13：
a 为正数，函数开口向上：a 的绝对值越大，开口越小
a 为负数，函数开口向下：a 的绝对值越大，开口越小

2. 两根式，图（b）
   如果 f(x) = 0 存在两个实数根的话，两次函数可以写成两根式；
   \(f(x) = a(x - r_{1})(x - r_{2}), a \ne 0\)

3. 顶点式，图（c）
   \(f(x) = a(x - h)^{2} + k, a \ne 0\)
   
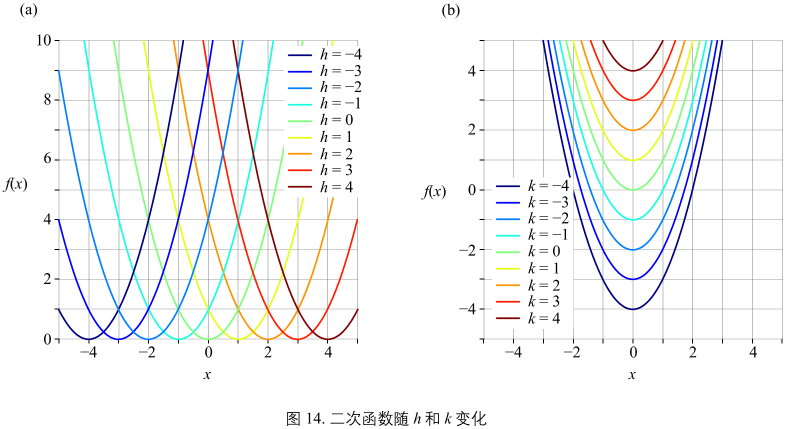
   图14（a）：
   函数图像和 h 的关系，h影响函数在水平方向位置。

图14（b）：
函数图形和 k 的关系，k影响函数在竖直方向位置。

11.4 多项式函数：从叠加角度来看

多项式函数相当于一次和二次函数的推广：
\(y = f(x) = a_{K}x^{K} + a_{K-1}x^{K-1} + ... + a_{2}^x{2}+a_{1}x + a_{0} = \sum_{i=0}^{K}a_{i}x^{i}\)

最高次系数 \(a_{K}\) 不为 0，\(x^{K}\) 中的 K 为最高次项次数

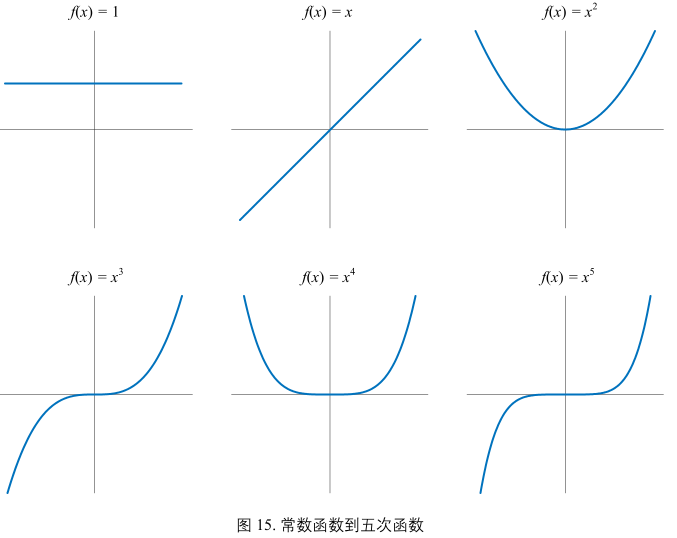
三次函数

\(y = f(x) = a_{3}x^{3} + a_{2}x^{2} + a_{1}x + a_{0}\)

举例：

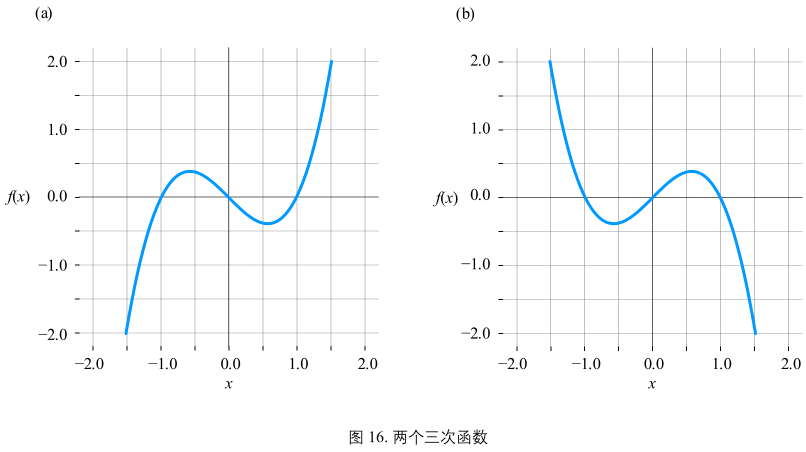
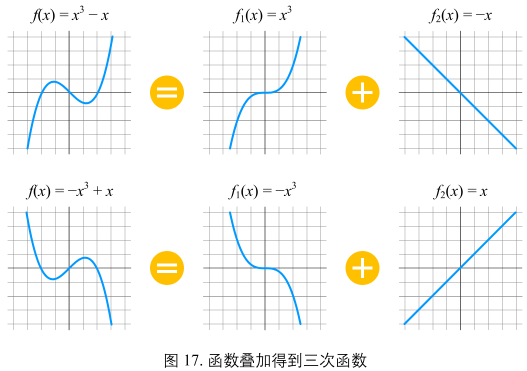
图16（a） + 图17（上）：
\(y = f(x) = x^{3} - x\)

图16（b） + 图17（下）：
\(y = f(x) = -x^{3} + x\)

11.5 幂函数：底数为自变量

\(f(x) = k * x^{p}\)
x：底数
p：指数

常用的幂函数：

1. 常函数：\(f(x) = 1 = x^{0}\)
   

2. 恒等函数：\(f(x) = x = x^{1}\)
   

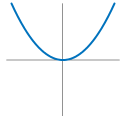
3. 平方函数：\(f(x) = x^{2}\)
   

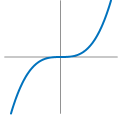
4. 立方函数：\(f(x) = x^{3}\)
   

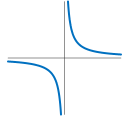
5. 反比例函数：\(f(x) = \frac{1}{x} = x^{-1}\)
   

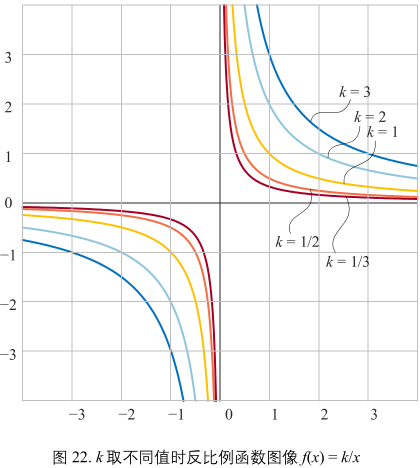
• 还有一种形式：\(y = f(x) = \frac{k}{x}\)
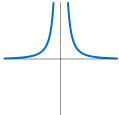
  图22：
  

|k| > 1 时，双曲线远离原点方向拉伸；|k|<1 将双曲线靠近原点方向压缩。

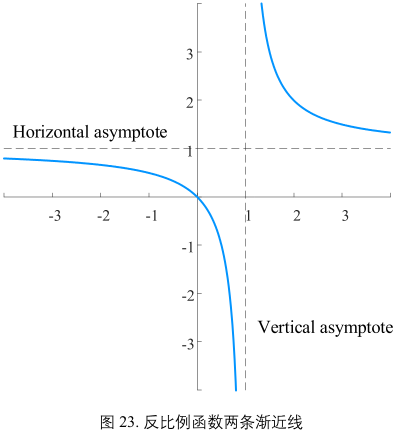
• 移动后可以得到简单的有理函数：\(f(x) = \frac{k}{x - h} + a\)
  其中 \(x \ne h\)
  h 左右移动竖直渐近线；a 上下移动水平渐近线。

图23：\(f(x) = \frac{1}{x + 1} + 1\)

5. 反比例平方函数：\(f(x) = \frac{1}{x^{2}} = x^{-2}\)
   

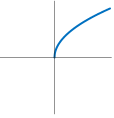
6. 平方根函数：\(f(x) = \sqrt{x} = x^{\frac{1}{2}}\)
   

7. 立方根函数：\(f(x) = \sqrt[3]{x} = x^{\frac{1}{3}}\)
   

奇偶性

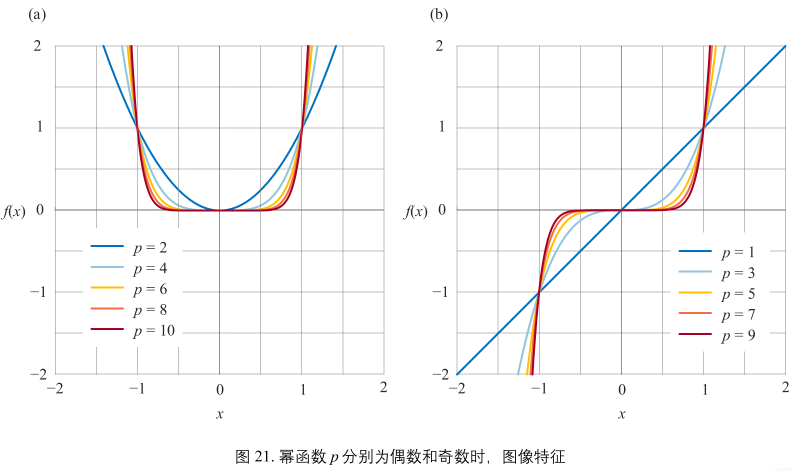
图21（a）：
p 为偶数，幂函数为偶函数，图像关于 y 轴对称。P 值越大，x 绝对值增大时，函数值快速接近正无穷

图21（b）：
p 为奇数，幂函数为奇函数，图形关于 原点对称。P 值越大，x 绝对值增大时，函数值越快接近正无穷或负无穷。

渐近线#

曲线极限相关的一条直线，当曲线上某动点沿该曲线的一个分支移向无穷远时，动点到该渐近线的垂直举例趋于0.

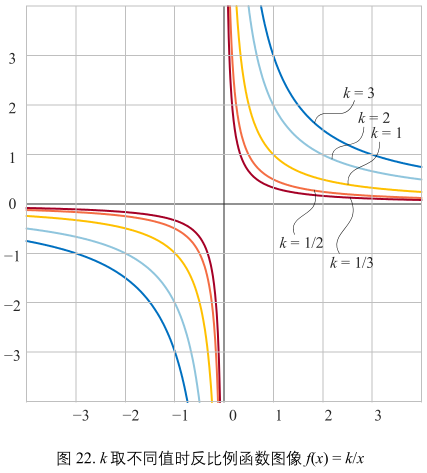
图22，当 x 从右侧接近竖直渐近线，函数值无约束的接近正无穷；相反当 x 从左侧接近竖直渐近线，函数值无约束的接近负无穷。

11.6 分段函数：不连续函数

分段函数式一类不连续函数；分段函数是自变量 x 的不同的取值范围有不同的解析式的函数
图24：

$
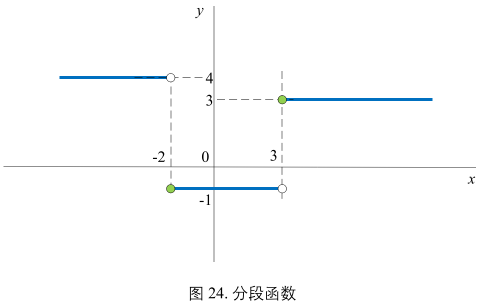
\begin{cases}

4 & x < -2 \
-1 & -2 <= x < 3 \
3 & 3 <= x

\end{cases}
$

图25：

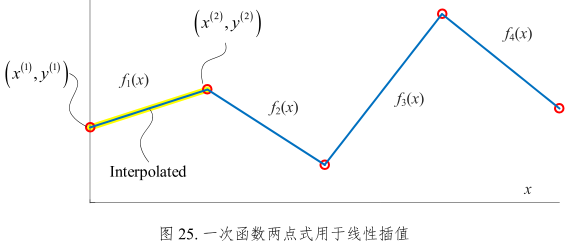
所有红色的圆点为已知离散数据点。
相邻亮点连接得到的线段解析式是线性插值分段函数。两点式公式常用在线性插值。
举例：利用一次函数两点式，给定两点\((x^{1}, y^{1})\) 和 \((x^{2}, y^{2})\) 可以确定分段函数 \(f_1(x)\)

插值指的是通过已知离散数据点，在一定范围内推导求得新数据点的方法。线性插值是指插值函数为一次函数。

插值函数是分段函数时，也称分段插值，每两个相邻的数据点之间便是一个分段函数：
$
\begin{cases}

f_{1}(x) & x^{1} <= x < x^{2} \

f_{2}(x) & x^{2} <= x < x^{3} \

... & ... \

f_{n-1}(x) & x^{n-1} <= x < x^{n}

\end{cases}
$

绝对值函数

可以看作是分段函数，一般式：\(f(x) = k|x - h| + a\)

图26

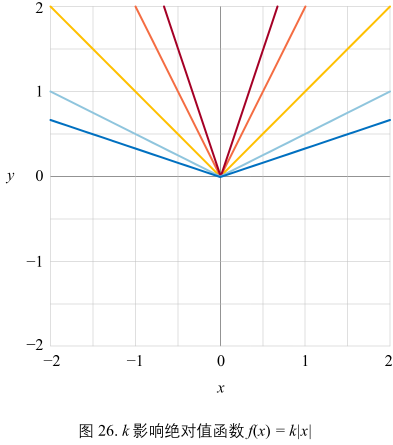
举个简单的例子：\(f(x) = k|x|\)
x = 0 为 f(x) 的尖点，它破坏了函数的光滑；
k 影响开口大小；k 的绝对值越大，开口越小。

绝对值函数可以写成自变量的指数幂和开方形式：
\(f(x) = \sqrt[k]{x^{2}}\)

注：以上内容均摘自生姜博士的鸢尾花书系列-Book_3《数学要素》