鸢尾花书 - Book_3《数学要素》 - Chapter10 函数

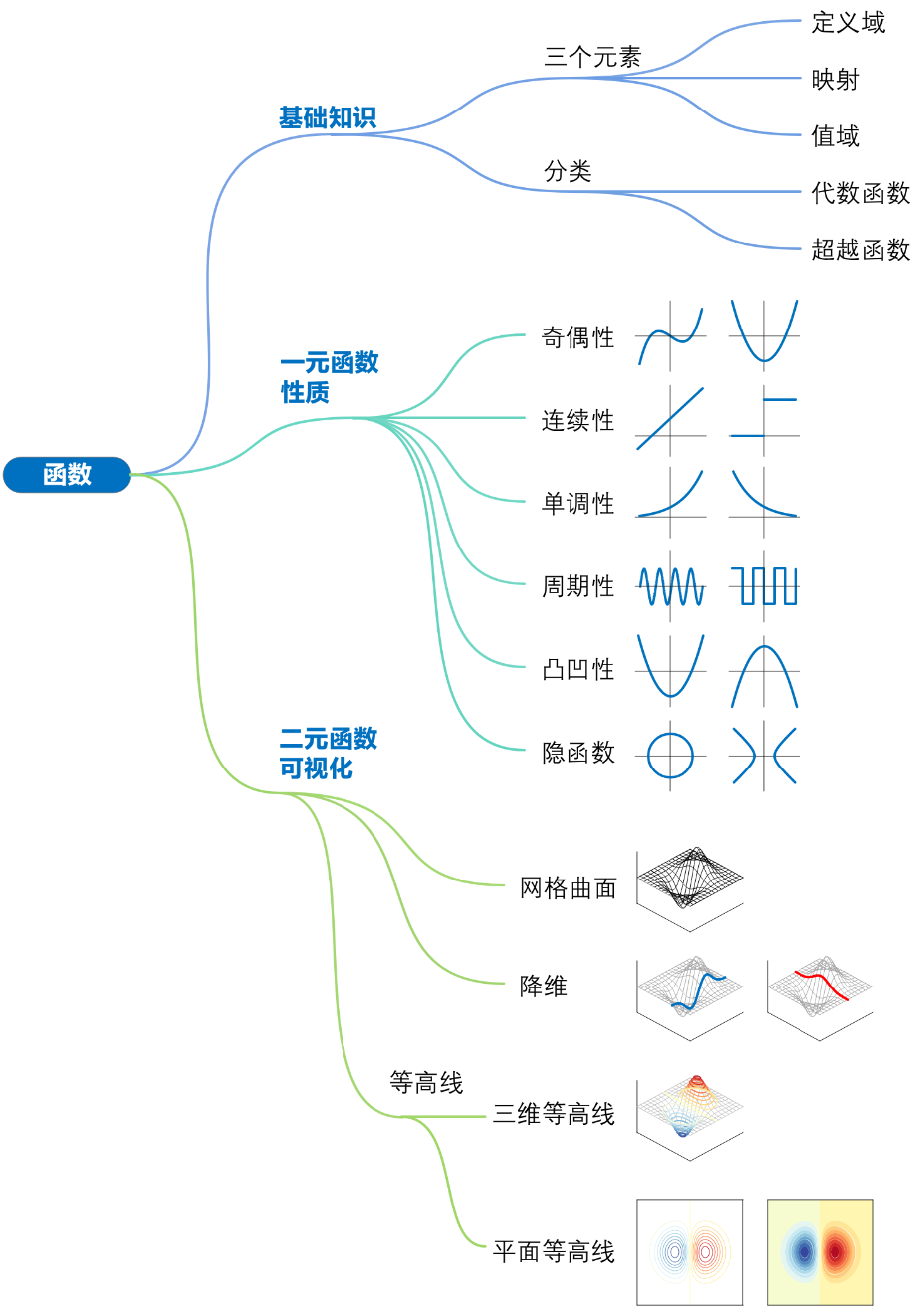
10.1 待代数式遇到坐标系

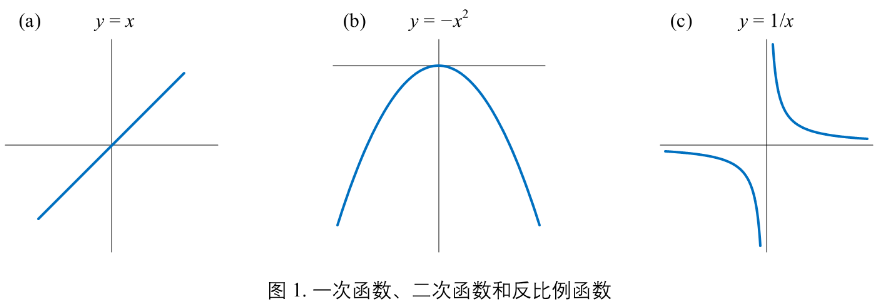
第一组

1. 线性函数 \(y = x\)

2. 抛物线 \(y = -x^{2}\)

3. 反比例函数 \(y = \frac{1}{x}\)

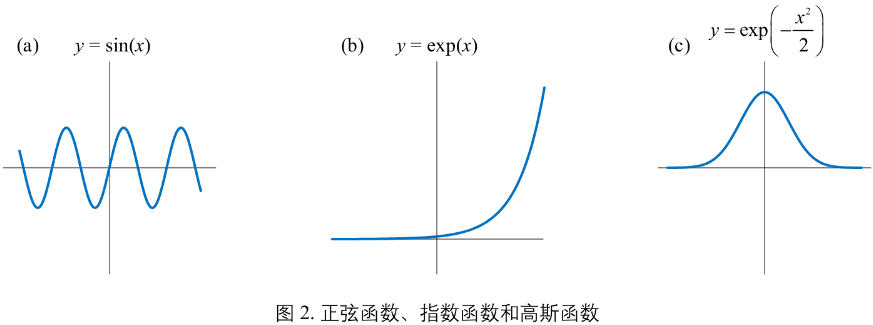
第二组

1. 正弦函数 \(y = sin(x)\)

2. 指数函数 \(y = exp(x)\)

3. 高斯函数 \(y = exp(-\frac{x^{2}}{2})\)

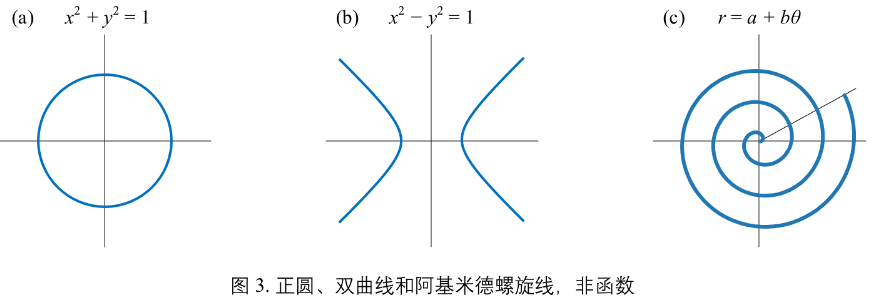
第三组

1. 正圆 \(x^{2} + y^{2} = 1\)

2. 双曲线 \(x^{2} - y^{2} = 1\)

3. 阿基米德螺旋线 \(r = a + b\theta\)

10.2 一元函数：一个自变量

定义

函数 f 以 x 作为唯一输入值，输出值写作 \(y = f(x)\)，函数是一元函数。有一个自变量的函数叫做一元函数。

定义域：x 构成的集合
值域：y 构成的集合

注意：任一 x 在值域中有唯一对应的 y。不同的 x 可以对应不一样的函数值。

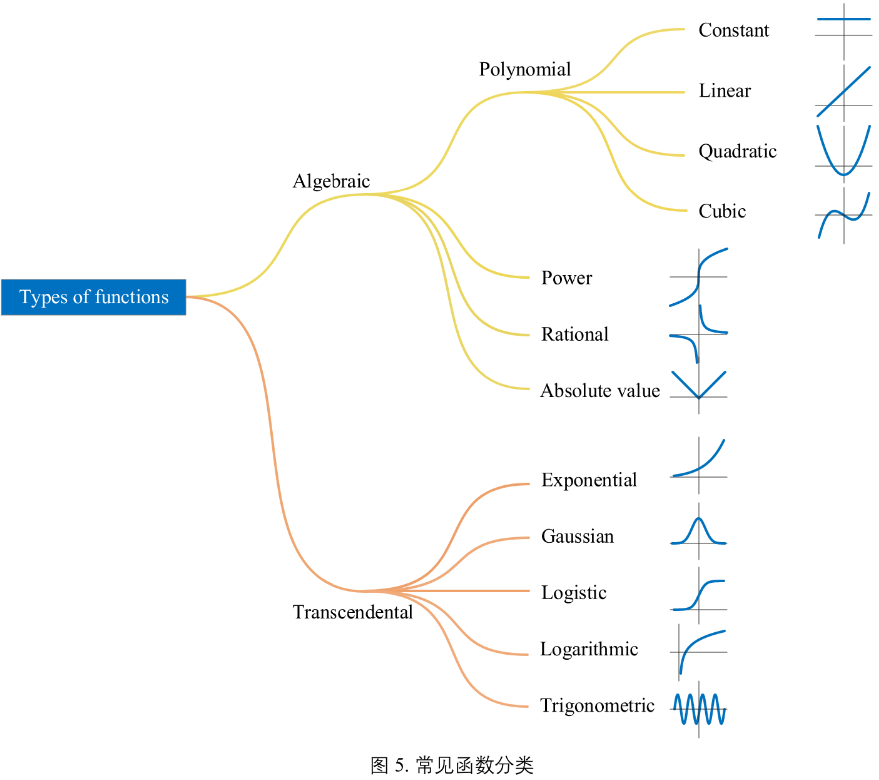
代数函数

定义：通过与自变量相互之间有限加、减、乘、除、有理指数幂和开方等运算构造的函数。

超越函数

定义：“超出”代函数范畴的函数，比如对数函数、指数函数、三角函数

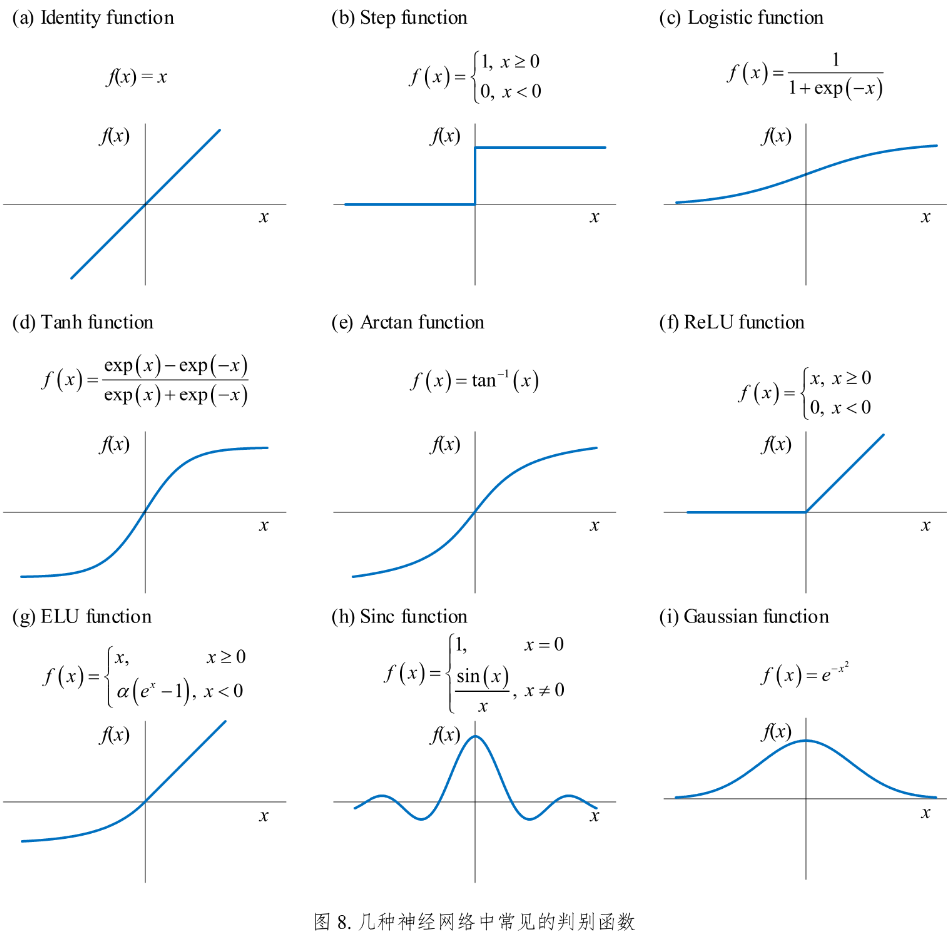
10.3 一元函数的性质

学习函数时，关注函数特征：1. 形状；2. 变化趋势；3. 自变量取值范围；4. 函数值取值范围；5. 函数性质

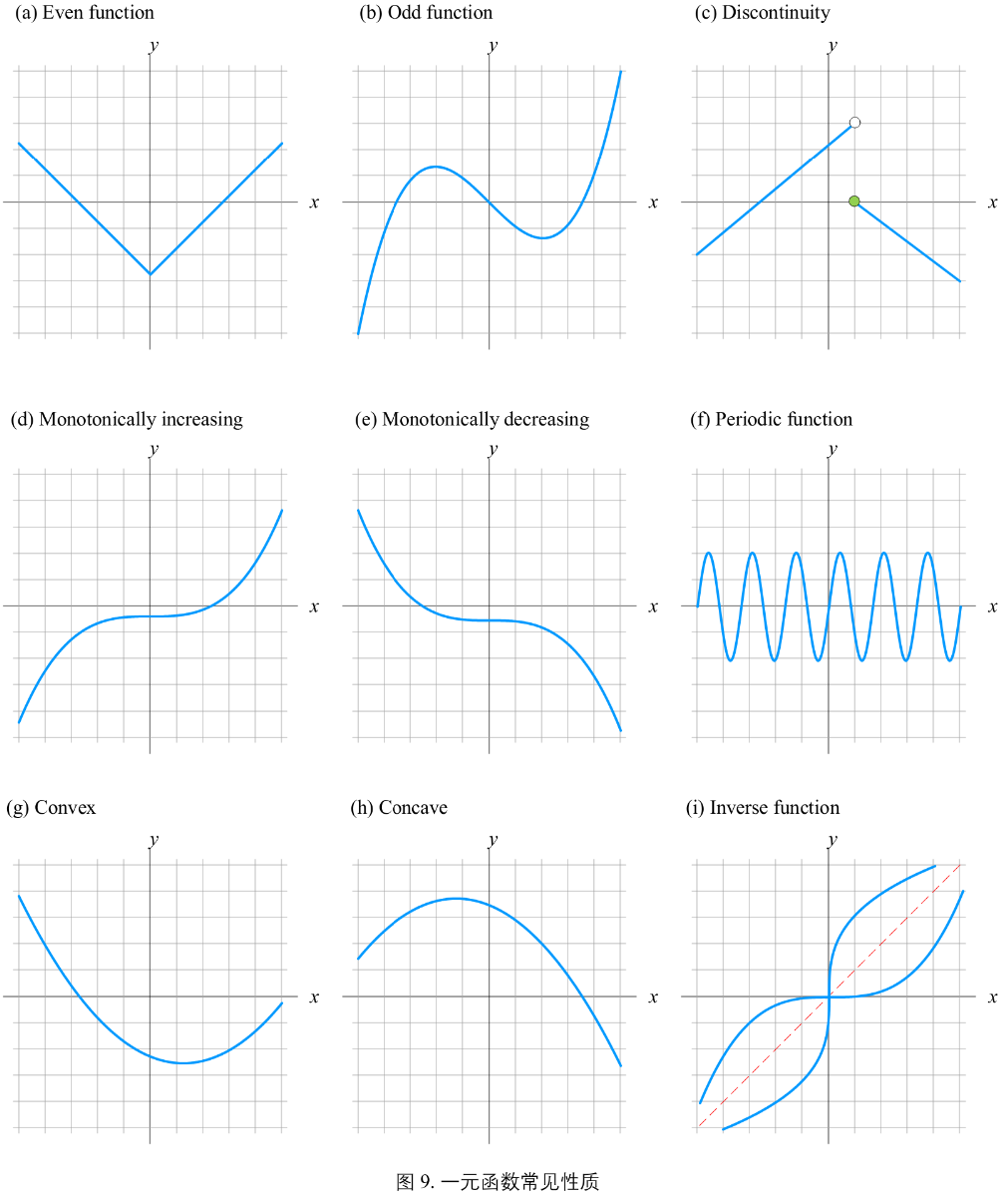
1. 奇偶性

图9（a）
f(x) 若为偶函数，对于定义域内任意 x 关系都成立：\(f(x) = f(-x)\)，关于纵轴对称。

图9（a）
f(x) 若为奇函数，对于定义域内任意 x 关系都成立：\(f(-x) = -f(x)\)，关于原点对称。

2. 连续性

函数 \(y = f(x)\) 当自变量 x 的变化很小时，所引起的因变量 y 的变化很小，即没有函数值突变。

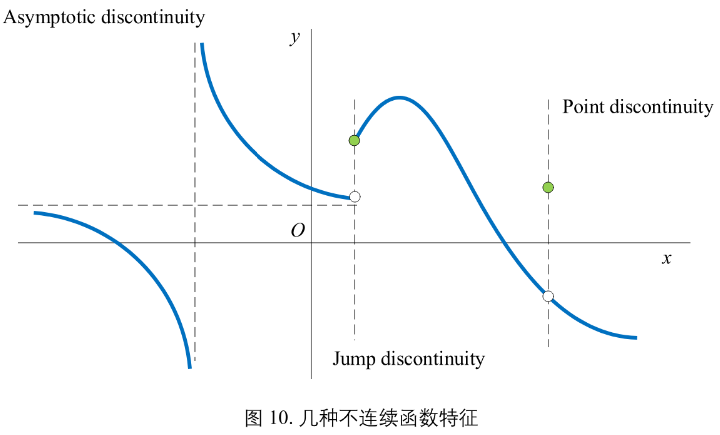
图9（c）不连续。1. 渐近线间断（asymptotic discontinuity）；2. 点间断（point discontinuity）；3. 跳跃简短（jump discontinuity）

3. 单调性

图9（d）单调增；图（e）单调减

4. 周期性

图9（f）
函数 f 中不同位置 x 满足 \(f(x+T) = f(x)\)，T为周期。

5. 凹凸性

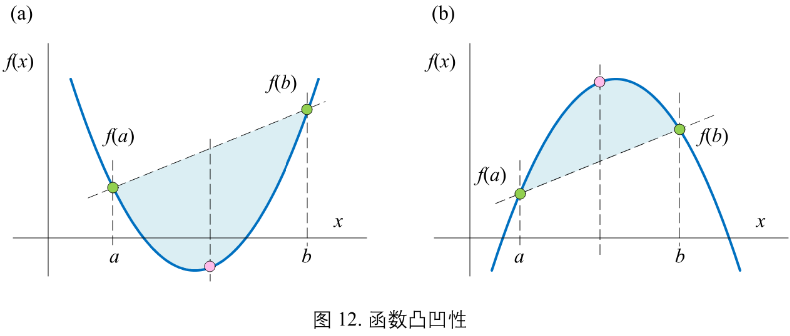
图12（a）
若 f(x) 在区间 I 有定义，如果对于任意\(a, b \in I\) 且 \(a \ne b\)
如果满足：\(f(\frac{a + b}{2}) < \frac{f(a) + f(b)}{2}\)
则称 f(x) 在该区间内为凸函数

图12（b）
若 f(x) 在区间 I 有定义，如果对于任意\(a, b \in I\) 且 \(a \ne b\)
如果满足：\(f(\frac{a + b}{2}) > \frac{f(a) + f(b)}{2}\)
则称 f(x) 在该区间内为凹函数

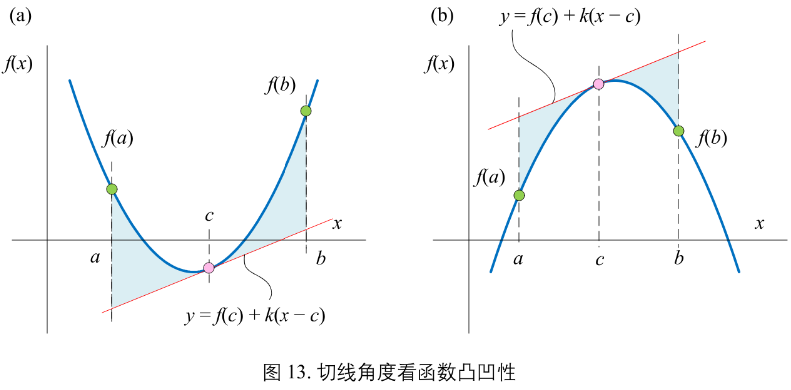
图13
在（a, b）区间内一点 x = c，在函数(f, f(c))做一条切线，解析式：\(y = f(c) + k(x - c)\)，k就是函数在 x = c 切线的斜率。

图13（a）
如果函数是凸函数，当 \(x \ne c\)，函数 f(x) 的图像在切线上方，即：
\(f(x) > f(c) + k(x - c), x \in (a, b), x \ne c\)

图13（b）
如果函数是凹函数，当 \(x \ne c\)，函数 f(x) 的图像在切线下方，即：
\(f(x) < f(c) + k(x - c), x \in (a, b), x \ne c\)

6. 反函数

\(x = f^{-1}(y)\) 定义域 = \(y = f(x)\) 值域
\(x = f^{-1}(y)\) 值域 = \(y = f(x)\) 定义域

图9（i）
函数 f 和其反函数 \(f^{-1}\)，两者关系：\(f^{-1}(f(x)) = x\)

7. 隐函数

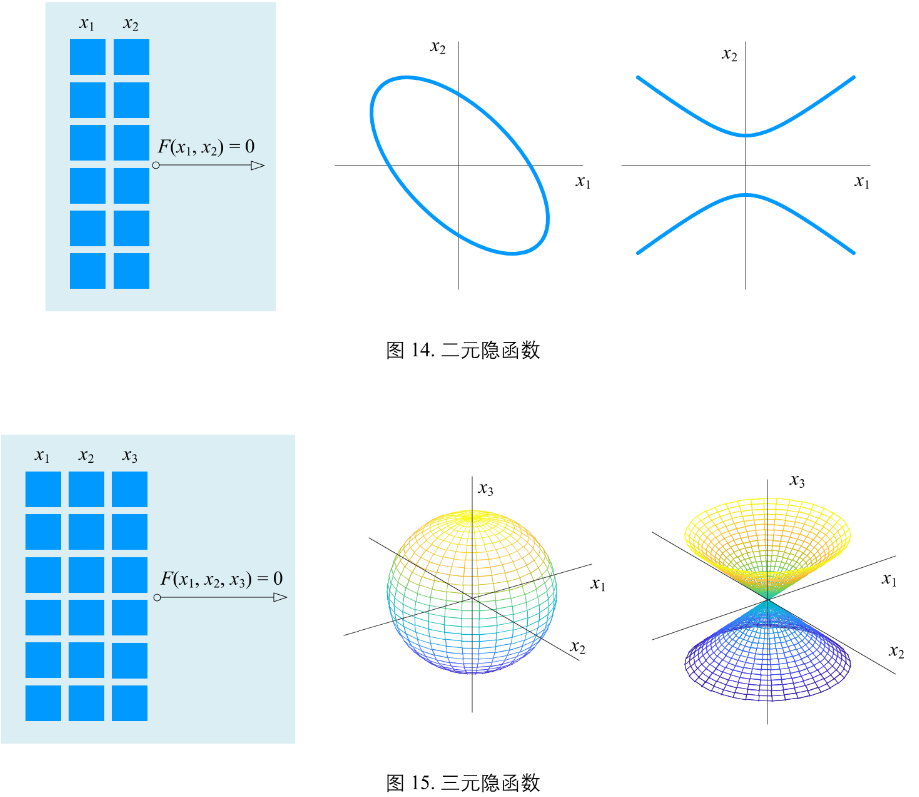
由隐式方程所隐含定义的函数，隐式方程F(x1, x2) = 0，描述 x1 和 x2 两者关系

不同于一般函数，很多隐函数较难分离自变量和因变量，如图14：

8. 变化率和面积

很多数学问题要求准确的函数变化率。

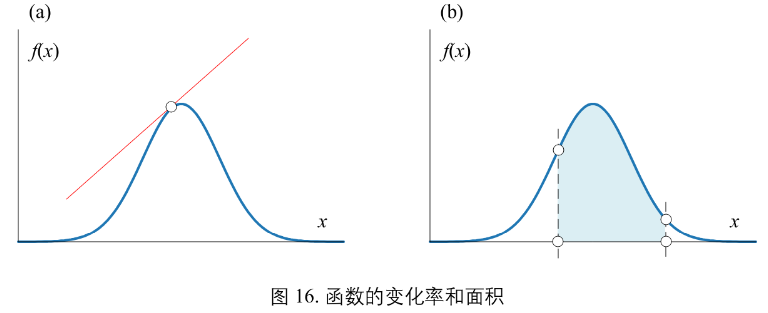
图16（a）
函数上某一带你切线的斜率是函数的变化率。微积分中，函数的变化率称为导数。

图16（b）
一些数学问题求解面积时，需要计算某个函数图形在一定取值范围和横轴围城几何图形的面积，这就需要用到积分。

图17

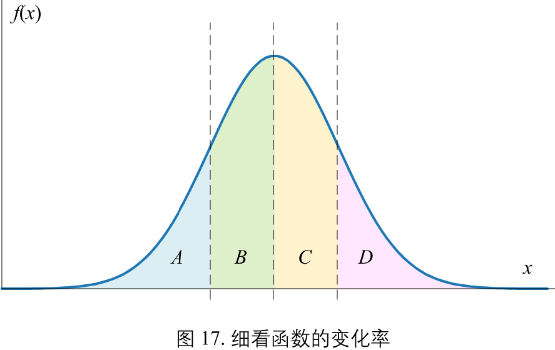
在A B 两个区域，随 x 增大 f(x) 增大，变化率为正。在A B两个区域在函数曲线上任一点做切线，切线斜率为正。

在 A 区域，x 增大 f(x) 增速加快，函数“变化率的变化率”为正；
在 B 区域，x 增大 f(x) 增速放缓，函数“变化率的变化率”为负；

在C D区域，随 x 增大 f(x) 减小，变化率为负。在C D两个区域在函数曲线上任意一点做切线，切线斜率为负。

10.4 二元函数：两个自变量

有两个自变量函数叫做二元函数，比如 \(y = f(x1, x2)\)

图18 所示为二元函数映射关系以及几个示例：

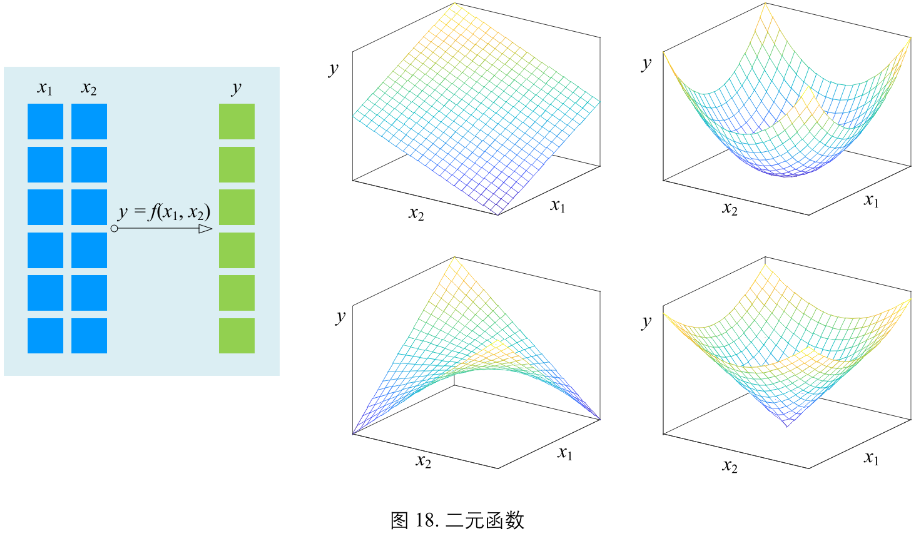
举例：二元一次函数 \(y = f(x_{1}, x_{2}\) = x1 + x2。x1 = 2, x2 = 4，函数值=6

网格化数据

为了获得 \(f(x_{1}, x_{2})\) 在三维空间的图形，需要提供一系列整齐的网格化坐标值（x_{1}, x_{2}）

将上述坐标点 x1 和 x2 分离并携程两个矩阵形式：

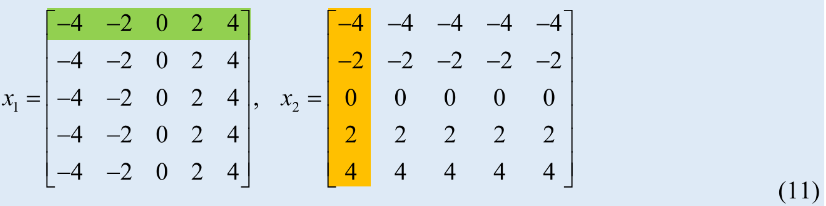
x1 的每个值代表点的横坐标
x2 的每个值代表点的纵坐标。
numpy.meshgrid() 获得网格化数据

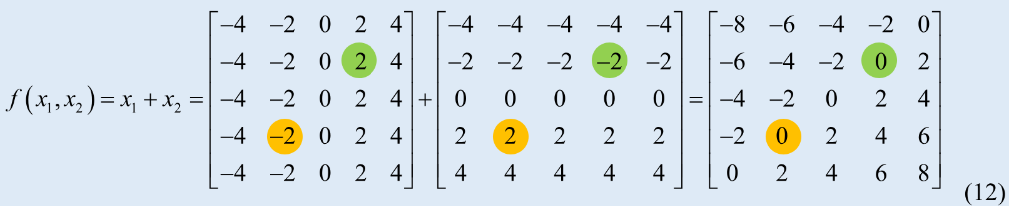
图19
f(x1, x2) = x1 + x2 对应的三维空间平面。
函数 f() 则代表某种规则，将网格数据从 x1x2 平面映射到三维空间

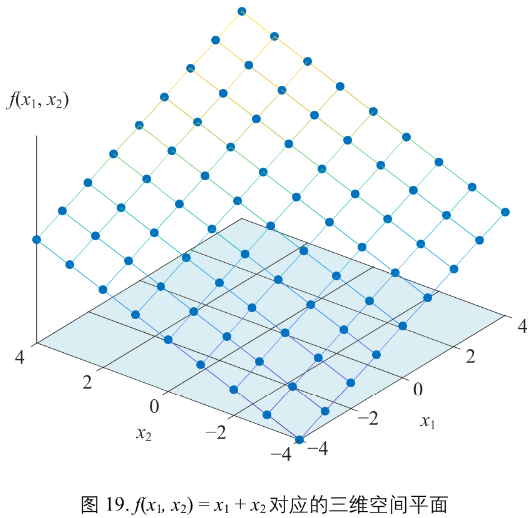
在绘制函数图像时，比如二元函数曲面，实际上输入的函数值都是离散的、网格化的。当然，网格越密，函数曲面越精确。实际应用中，网格的疏密可以根据函数的复杂度调整。对于复杂的函数，网格则需要设置的密一些，也就是步长小一些。

一个复杂曲面

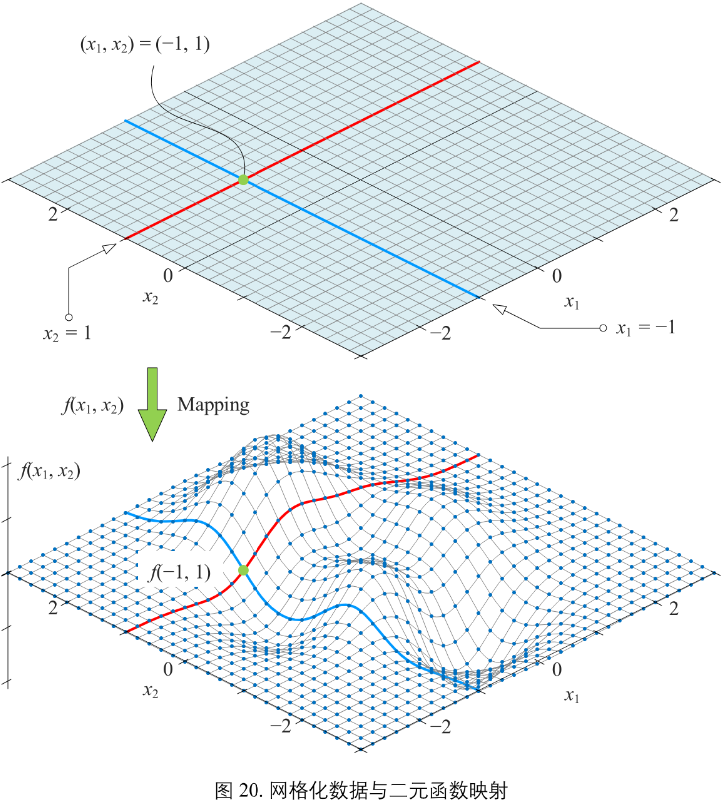
图20 函数解析式：
\(f(x_{1}, x_{2}) = 3(1-x_{1})^{2}exp(-x_{1}^{2}-(x_{2}+1)^{2})-10(\frac{x_{1}}{5}-x_{1}^{3}-x_{2}^{5})exp(-x_{1}^{2}-x_{2}^{2})-\frac{1}{3}exp(-(x_{1}+1)^{2}-x_{2}^{2})\)

10.5 降维：二元函数切一刀得到一元函数

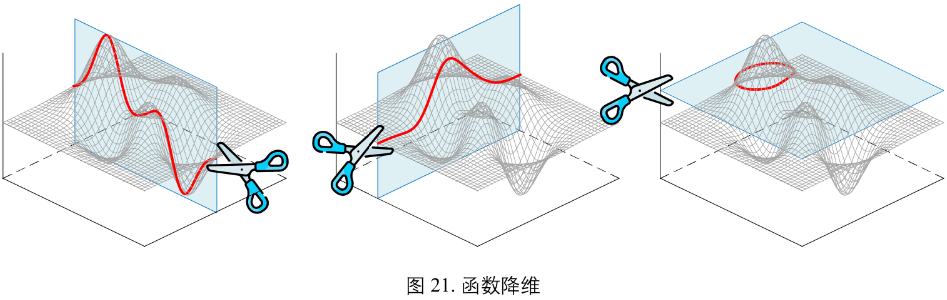
图21
二元函数两种可视化工具 - 剖面线、等高线

\(x_{1}y\) 平面方向剖面线

固定 x2 = c，自变量 x1 变化，f(x1, x2=c) 随 x1 变化的一元函数
图22：

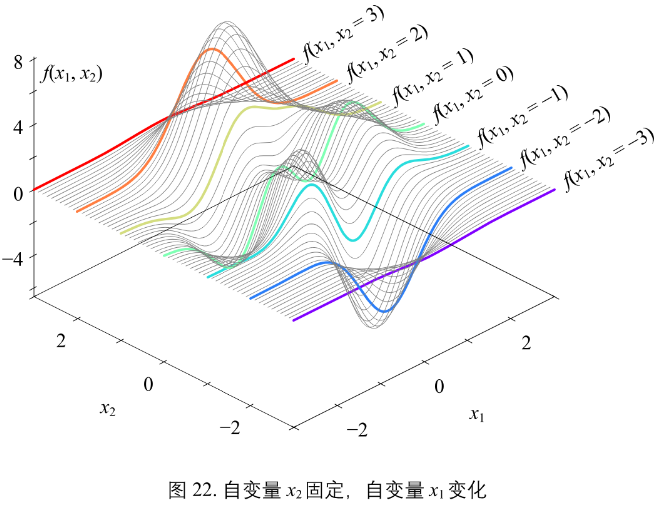
图23：
将 f(x1, x2=c) 剖面线投影在 \(x_{1}y\) 平面上。得到 图24

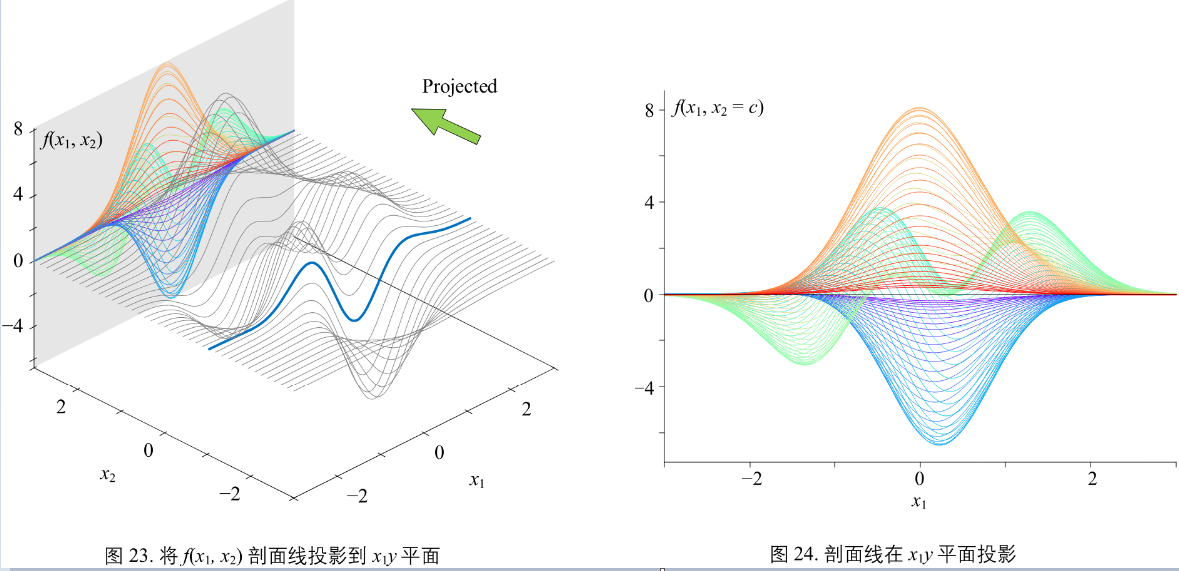
\(x_{2}y\) 平面方向剖面线

固定 x1 = c，自变量 x2 变化，f(x1=c, x2）随 x2 变化的一元函数

图25：

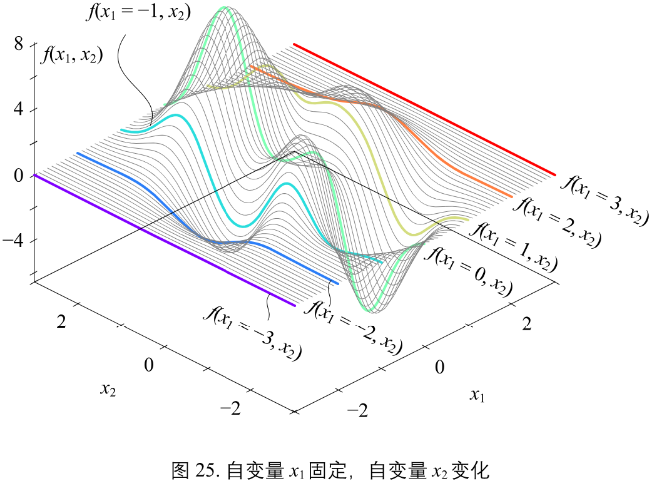
图26：
将 f(x1=c, x2) 剖面线投影在 \(x_{2}y\) 平面上。得到 图27

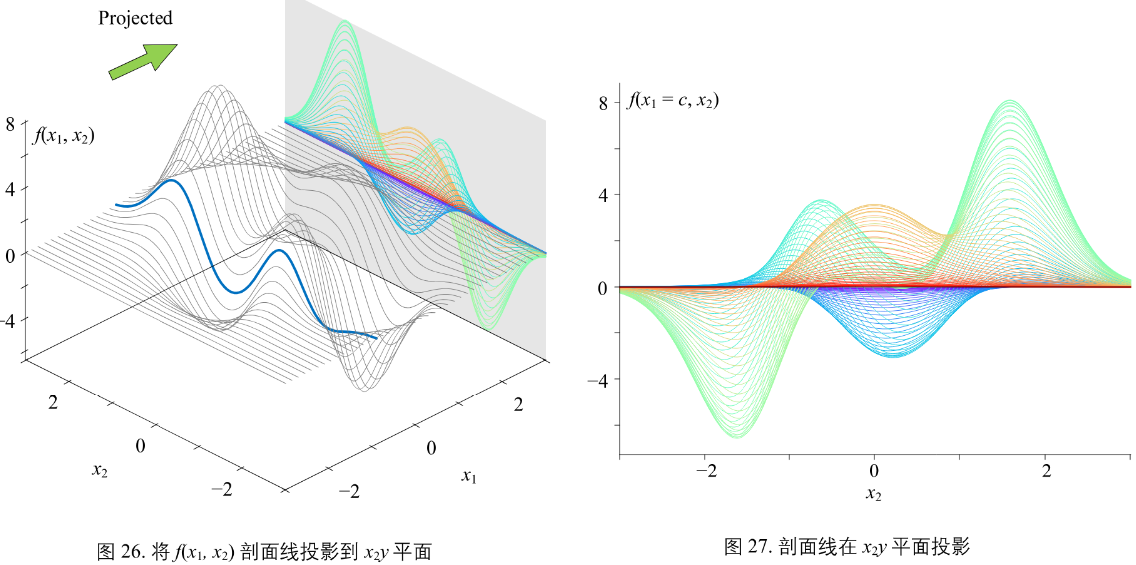
10.6 等高线：由函数值相等点连成

图28
f(x1, x2) 曲面比作一座山峰，函数值越大，相当于山峰越高。暖色山峰，冷色山谷。

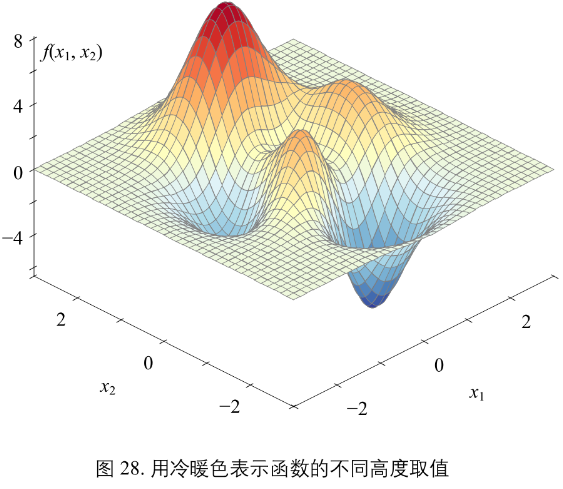
等高线

三维和平面等高线是研究二元函数重要的手段之一。
曲面某一条等高线是函数值 f(x1, x2)相同，即 f(x1, x2) = c 的相邻点连接构成的曲线。

图29
当 c 取值不同时，便得到一系列对应不同高度的等高线，这些曲线可以是闭合曲线，也可以非闭合

图30
将图29 所示彩色线投影到水平面上，得到平面等高线图。

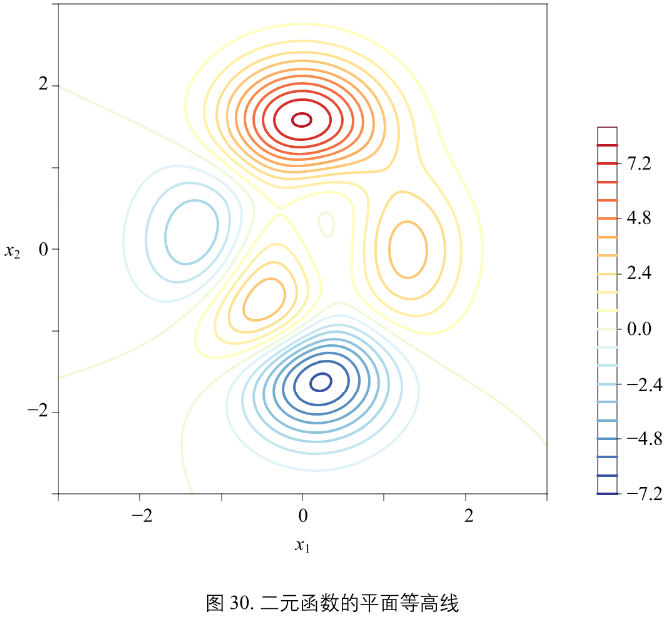
图中，每条不同颜色的曲线代表一个具体函数取值。把二元函数比作山峰的话，等高线越密集的区域，坡度越陡峭。等高线越平缓的区域，坡度越平坦。

填充等高线

图31

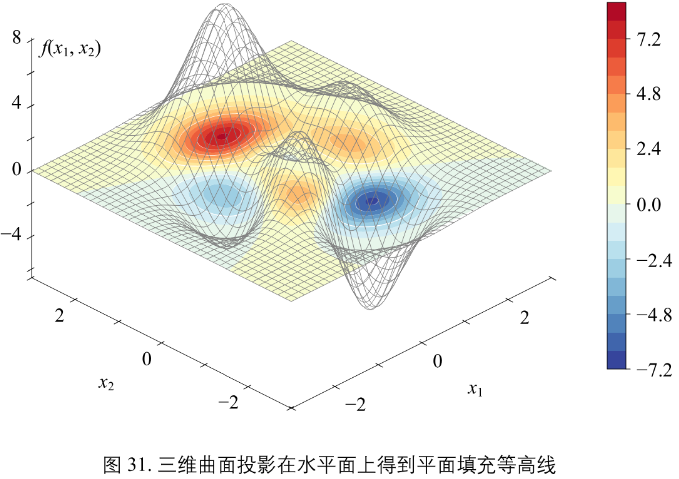
f(x1, x2) 三维坐标系中在 x1x2 平面上得到的填充等高线

图32

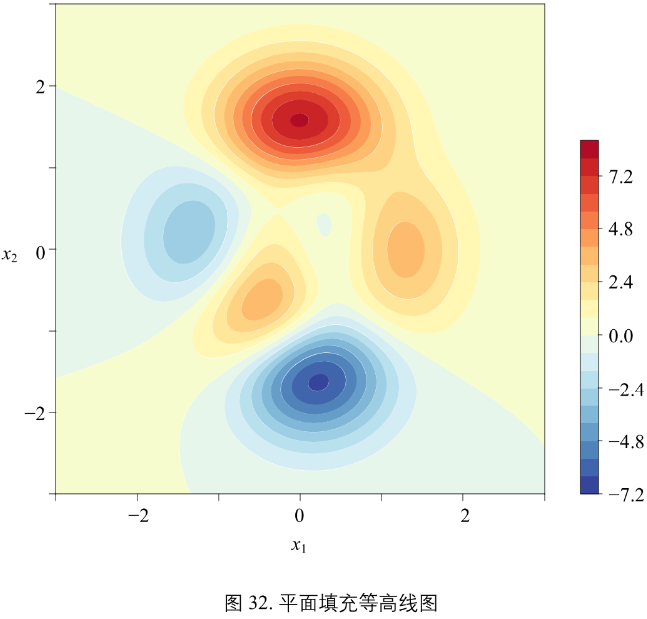
填充等高线在 x1x2 平面上的投影效果

注：以上内容均摘自生姜博士的鸢尾花书系列-Book_3《数学要素》