鸢尾花书 - Book_3《数学要素》 - Chapter9 深入圆锥曲线

9.2 离心率：联系不同类型的圆锥曲线

$x_{2}^{2} = 2px_{1} + (e^{2} - 1)x_{1}^{2}, x >= 0$ 公用（0, 0）顶点。
正圆离心率：e = 0
椭圆离心率：0 < e < 1
抛物线离心率：e = 1
双曲线离心率：e > 1
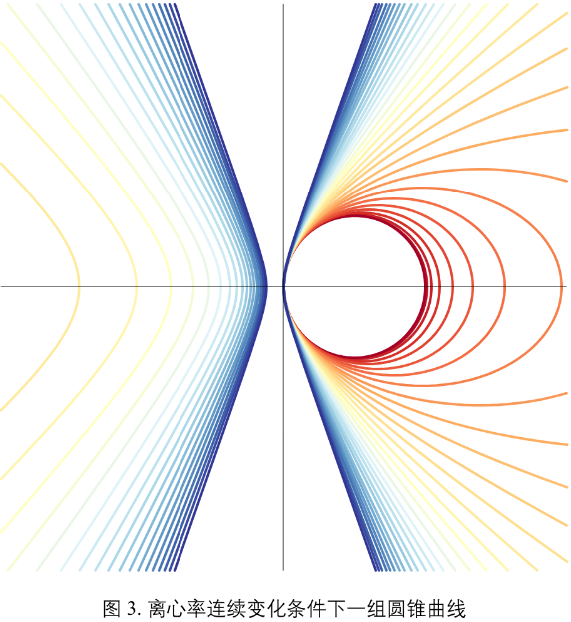
当 p = 1时，离心率 e 取不同数值，可以得到图3 一组圆锥曲线

9.3 一组有趣的圆锥曲线

解析式（2）：$\underbrace{\frac{x_{1}^{2}}{m^{2}} + \frac{x_{2}^{2}}{n^{2}}}_{\text Ellipse} - \underbrace{2\rho\frac{x_{1}x_{2}}{mn}}_{\text Hyperbola} = 1$ 其中，m > 0, n > 0。
上式可以看作是椭圆和双曲线的“叠加”。$x_{1}x_{2} = 1$ 实际上是一个旋转双曲线。参与 $\rho$ 可以视作调节双曲线“影响力”的参数， $\rho$ 越大双曲线的影响越强。
点 $(\pm m, 0)$、$(0, \pm n)$ 都满足上式，也就是说这四个点都在圆锥曲线上。

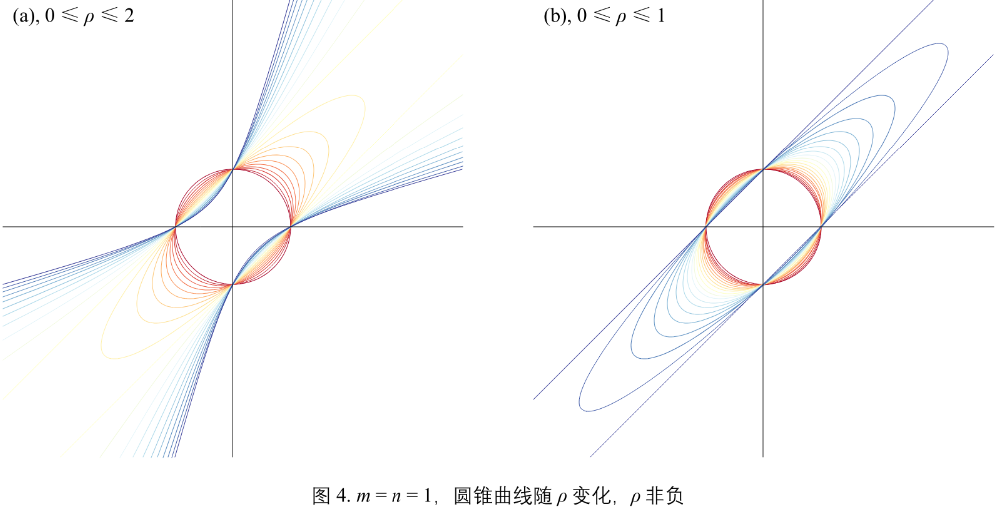
当 $m = n = 1$ 且 $\rho >= 0$，圆锥曲线随 $\rho$ 变化。
图4：

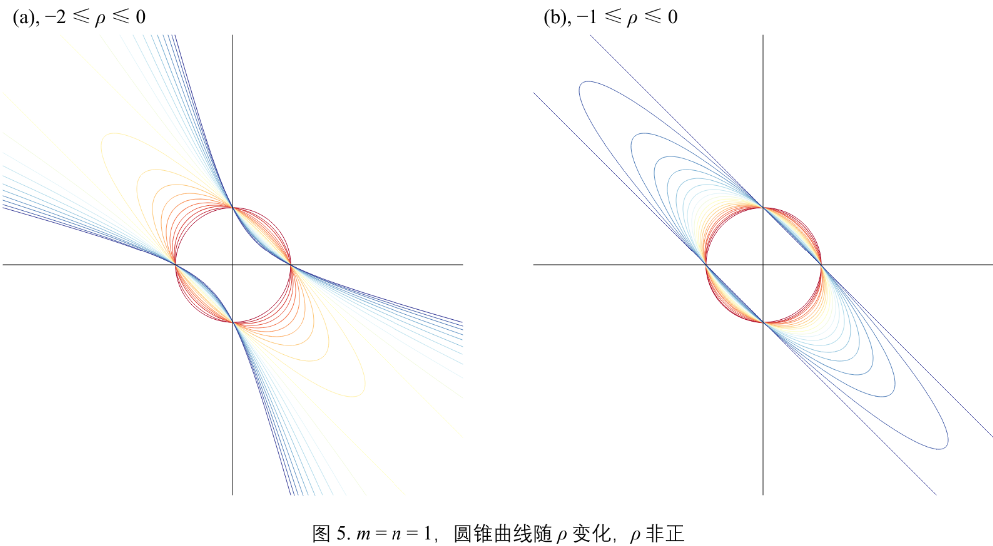
当 $m = n = 1$ 且 $\rho <= 0$，圆锥曲线随 $\rho$ 变化。
图5：

$-1 < \rho < 1$：椭圆的影响力占上风。
$\vert \rho \vert > 1$：双曲线影响力更大。
$\rho = \pm 1$：椭圆和双曲线势均力敌。

当 $m = n = 1$ 且 $\rho = 1$ 解析式（2）为 $(x - y)^{2} = 1$，对应两条直线 $x - y = 1, x - y = -1$

当 $m = n = 1$ 且 $\rho = -1$ 解析式（2）也对应两条直线

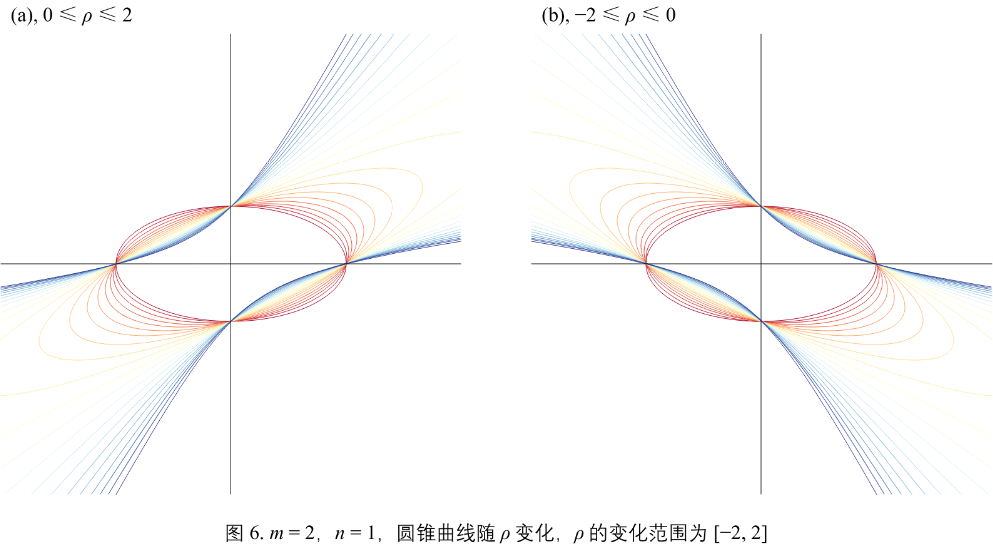
图6：m = 2, n = 1, 圆锥曲线随 $\rho$ 变化，$\rho$ 的变化范围为 [-2, 2]

9.4 特殊椭圆：和给定矩形相切

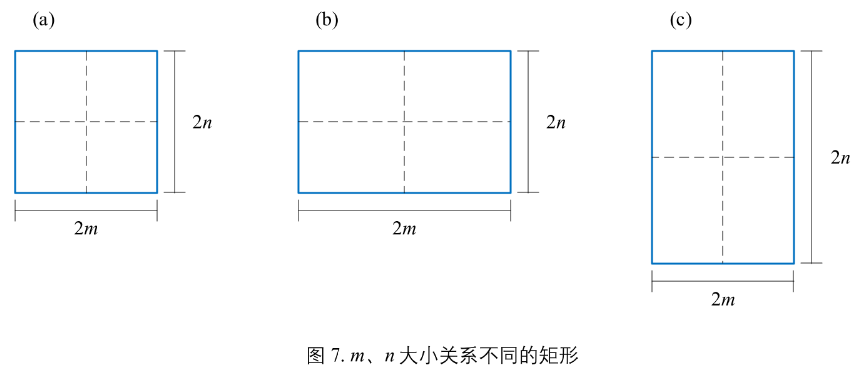
图7：假定三类矩形都位于原点。

对解析式（2）稍作修改：$\frac{x_{1}^{2}}{m^{2}} + \frac{x_{2}^{2}}{n^{2}} - \frac{2\rho x_{1}x_{2}}{mn} = 1 - \rho^{2}$ 解析式（5），$\rho$ 取值范围在 -1 和 1 之间。参数 $\rho$ 影响椭圆的倾斜程度

解析式（5）进一步写成：$\frac{1}{1-\rho^{2}}(\frac{x_{1}^{2}}{m^{2}} + \frac{x_{2}^{2}}{n^{2}} - \frac{2\rho x_{1}x_{2}}{mn}) = 1 - \rho^{2}$

图8：
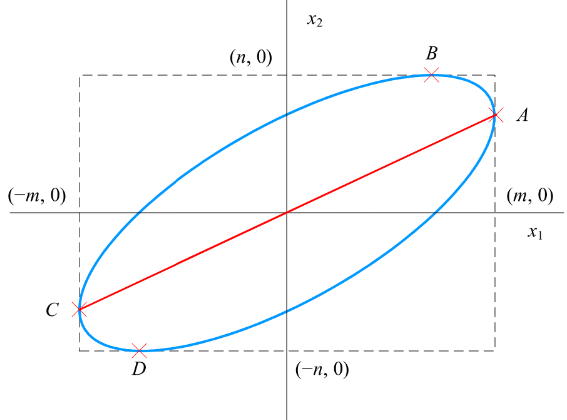
以矩形的中心为原点构建平面直角坐标系，容易计算得到矩形和椭圆相切的切点 A、B、C、D 的坐标为：$A(m, \rho n), B(\rho p, m), C(-m, -\rho n), D(-\rho m, -n)$

正椭圆

当 $\rho = 0$ 为正椭圆：$\frac{x_{1}^{2}}{m^{2}} + \frac{x_{2}^{2}}{n^{2}} = 1$
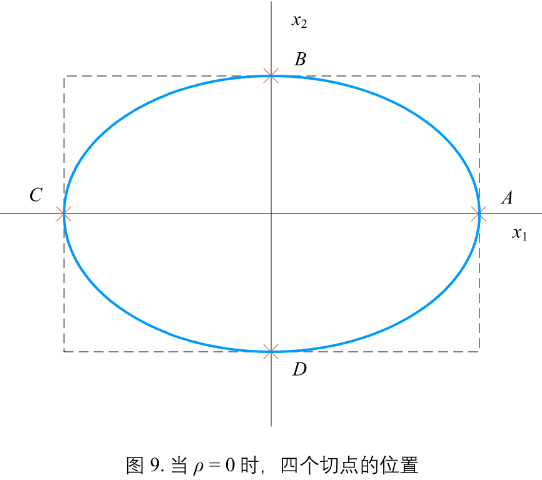
图9：椭圆和矩形相切的四个且带你A B C D 的坐标为：$A(m, 0), B(0, n), C(-m, 0), D(0, -n)$

线段

当 $\rho = 1$ 椭圆退化为一条线段
解析式：$\frac{x_{1}}{m} - \frac{x_2}{n} = 0$ （10）

当 $\rho = -1$ 椭圆也是一条线段
解析式：$\frac{x_{1}}{m} + \frac{x_{2}}{n} = 0$ （11）

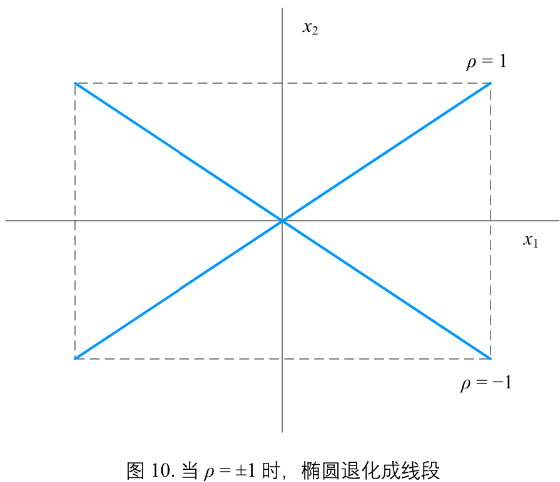
旋转椭圆

图11：m = n 椭圆形状随参数 $\rho$ 变化。$\rho$ 靠近0时，椭圆形状越接近正圆；$\rho$ 的绝对值越靠近 1，椭圆越扁；椭圆越扁，形状越接近线段。

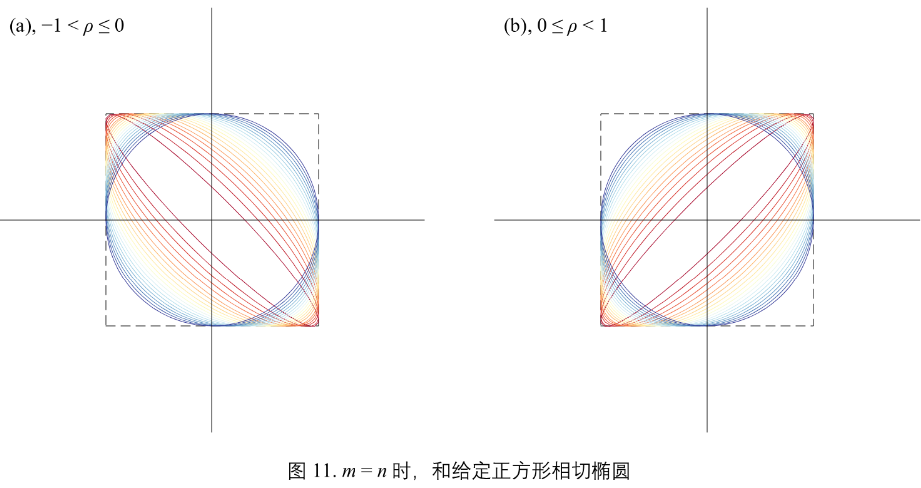
图12：m > n 椭圆形状随 $\rho$ 变化

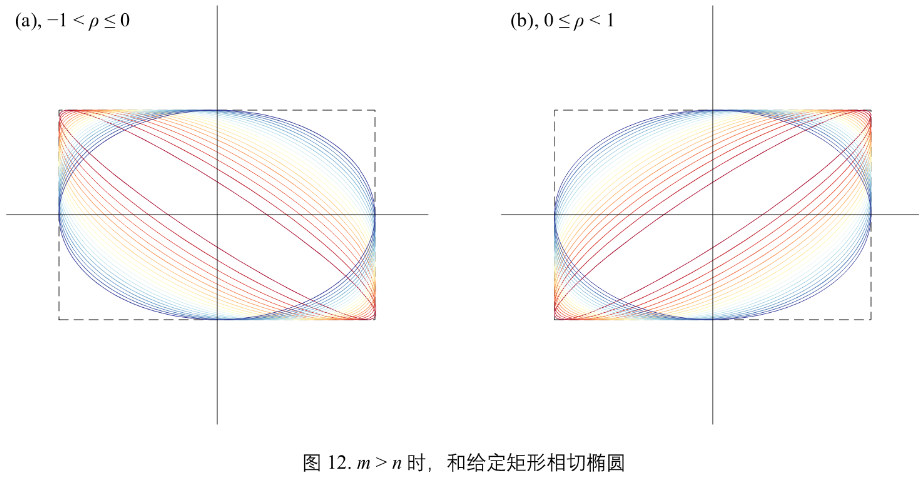
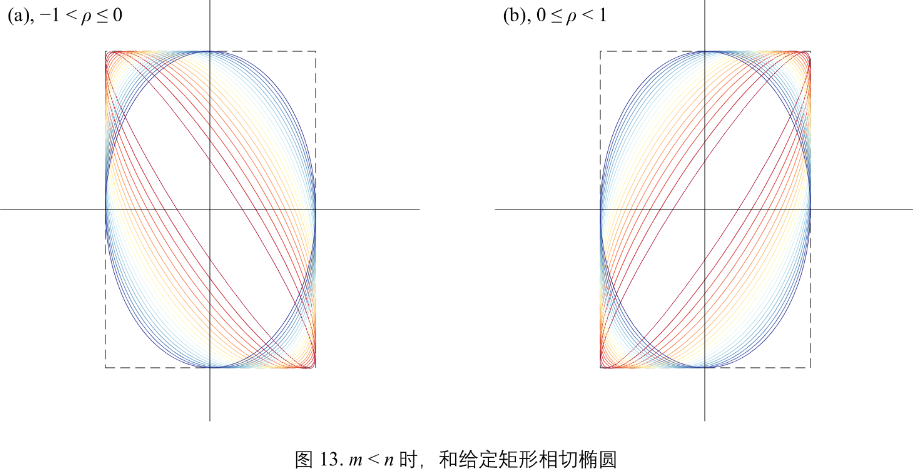
图13：m < n 椭圆形状随 $\rho$ 变化

二元高斯分布

之所以讨论特殊形态的椭圆，是因为它和二元高斯分布的概率密度函数直接相关。
解析式（12）：$ f_{x, y}(x, y) = \frac{1}{2\pi\sigma_{x}\sigma_{y}\sqrt{1-\rho^{2}_{x, y}}} \times \exp(\underbrace{\frac{-1}{2} \frac{1}{1-\rho^{2}_{x, y}} ((\frac{x-\mu_{x}}{\sigma_{x}})^{2} - 2\rho_{x, y} (\frac{x-\mu_{x}}{\sigma_{x}}) (\frac{y-\mu_{y}}{\sigma_{y}}) + (\frac{y-\mu_{y}}{\sigma_{y}})^{2}))}_{Ellipse} $
$\mu x$ 和 $\mu y$ 分别为随机变量 X，Y的期望值。

$\sigma x$ 和 $\sigma y$ 分别为随机变量 X，Y的均方差。

$\rho_{x, y}$ 为 X 和 Y 的线性相关系数，取值区间为(-1, 1)

9.5 超椭圆：和范数有关

最常见的超椭圆解析式（13）：$\vert \frac{x_{1}}{a} \vert^{p}+\vert \frac{x_{2}}{b} \vert^{p} = 1$ 一般情况 p > 0

当 p = 2，解析式（13）为椭圆解析式。
当 p = 1，超椭圆为菱形，解析式（14）：$\vert \frac{x_{1}}{a} \vert +\vert \frac{x_{2}}{b} \vert = 1$
当 p = +∞，超椭圆图形为长方形，解析式（15）：$max(\vert \frac{x_{1}}{a} \vert, \vert \frac{x_{2}}{b} \vert) = 1$

第一个例子

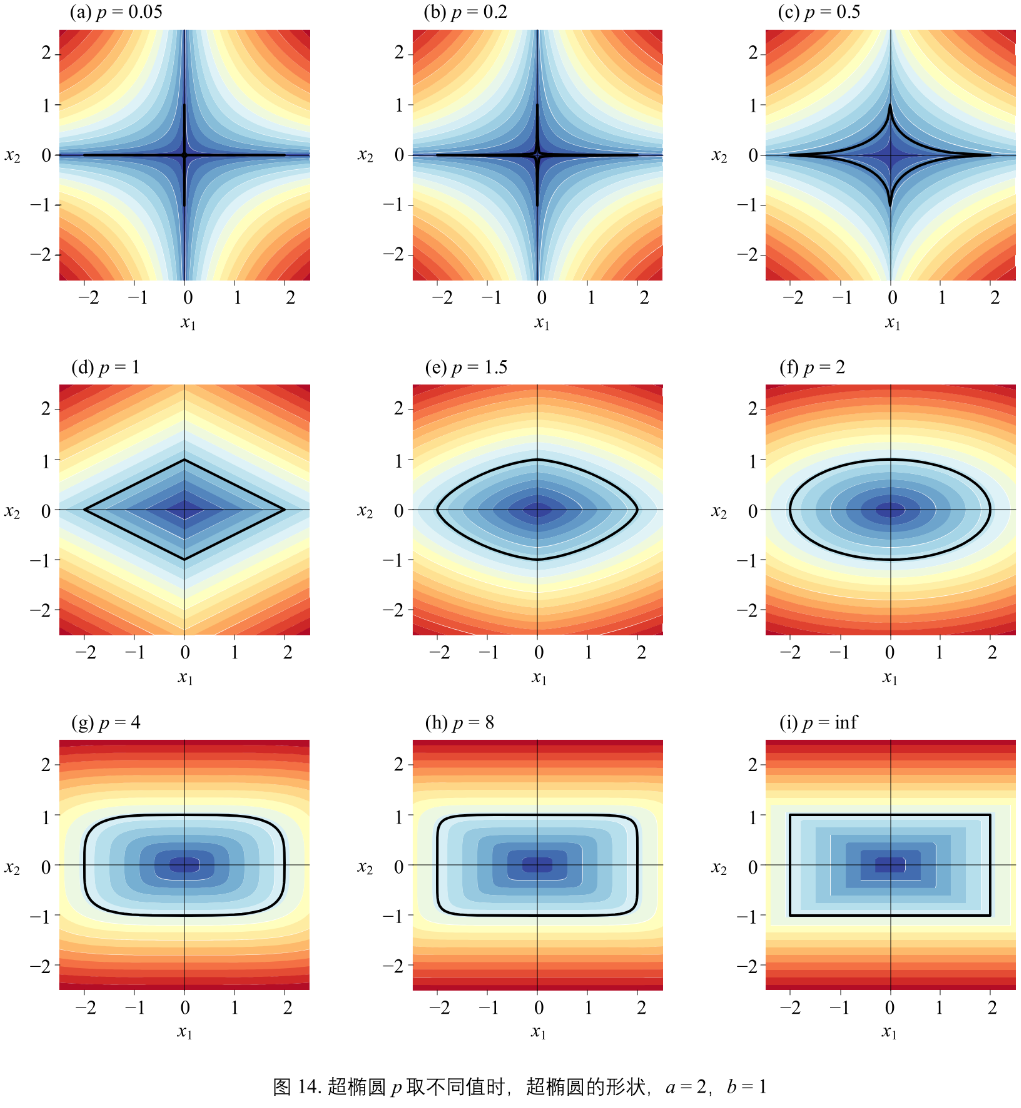
当 a = 2, b = 1，超椭圆解析式（16）：$\vert \frac{x_{1}}{a} \vert^{p} + \vert \frac{x_{2}}{b} \vert^{p} = 1$
图14 为 p 取不同值时，超椭圆的形状

第二个例子

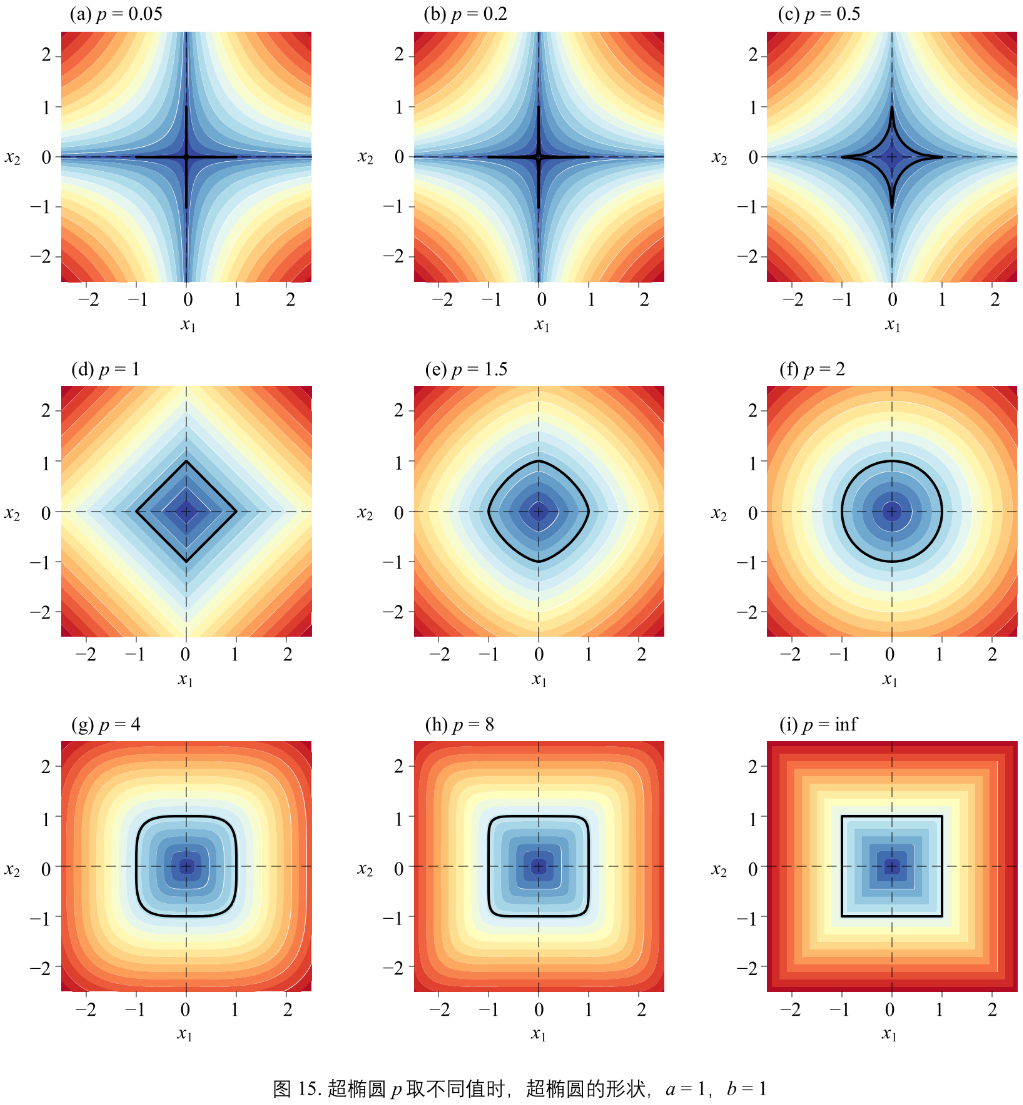
当 a = 1, b = 1，超椭圆解析式（17）：$\vert x_{1} \vert^{p} + \vert x_{2} \vert^{p} = 1$
图15 为 p 取不同值时，超椭圆的形状

p 和 q 两个参数

将解析式（13）进一步推广，得到二维平面的超椭圆解析式（18）：$\vert \frac{x_{1}}{a} \vert^{p}+\vert \frac{x_{2}}{b} \vert^{q} = 1$，其中 p 和 q 为正数

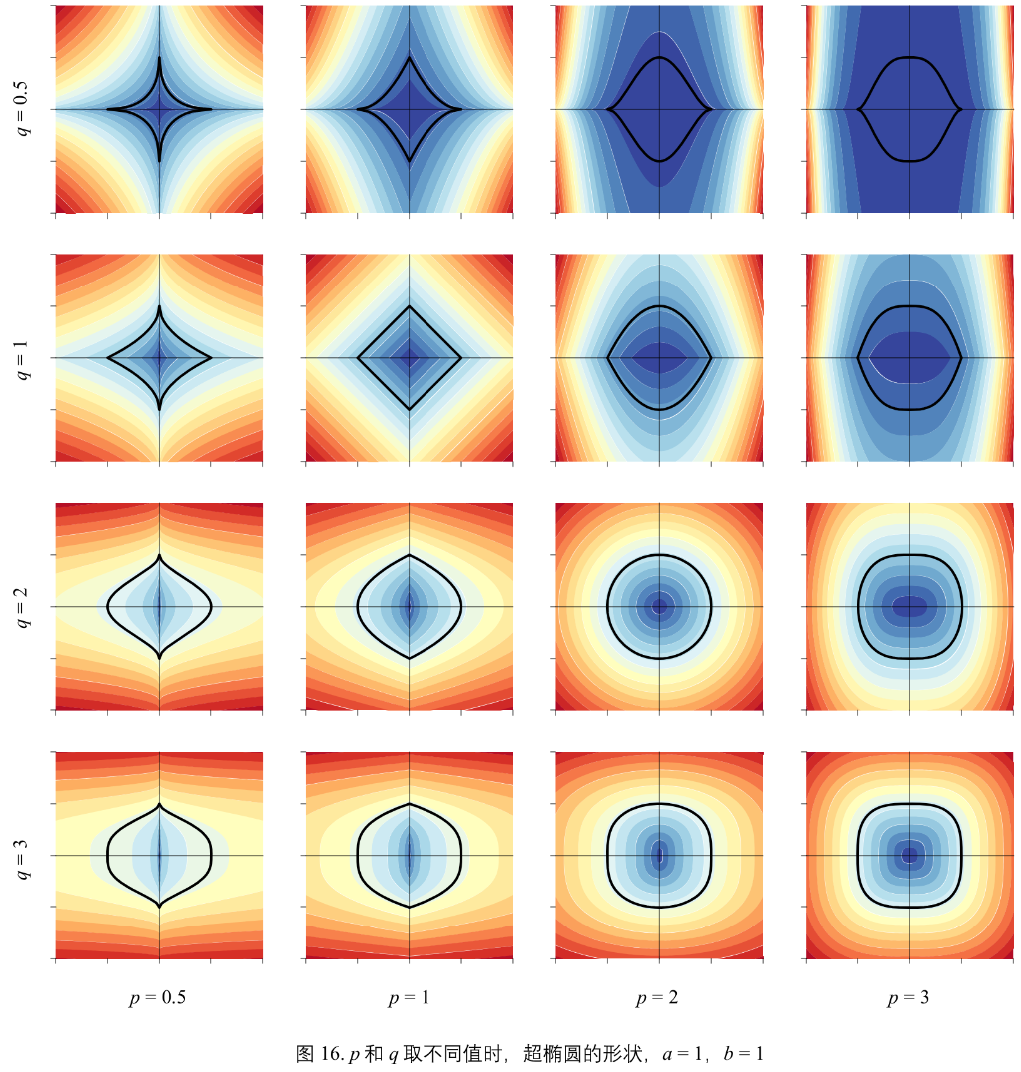
当 a = 1, b = 1, 解析式（18）对应的超椭圆解析式（19）为：$\vert x_{1}\vert^{p}+\vert x_{2}\vert^{q} = 1$
图16 为 p q 取不同值时，解析式（19）对应超椭圆的形状

超椭球

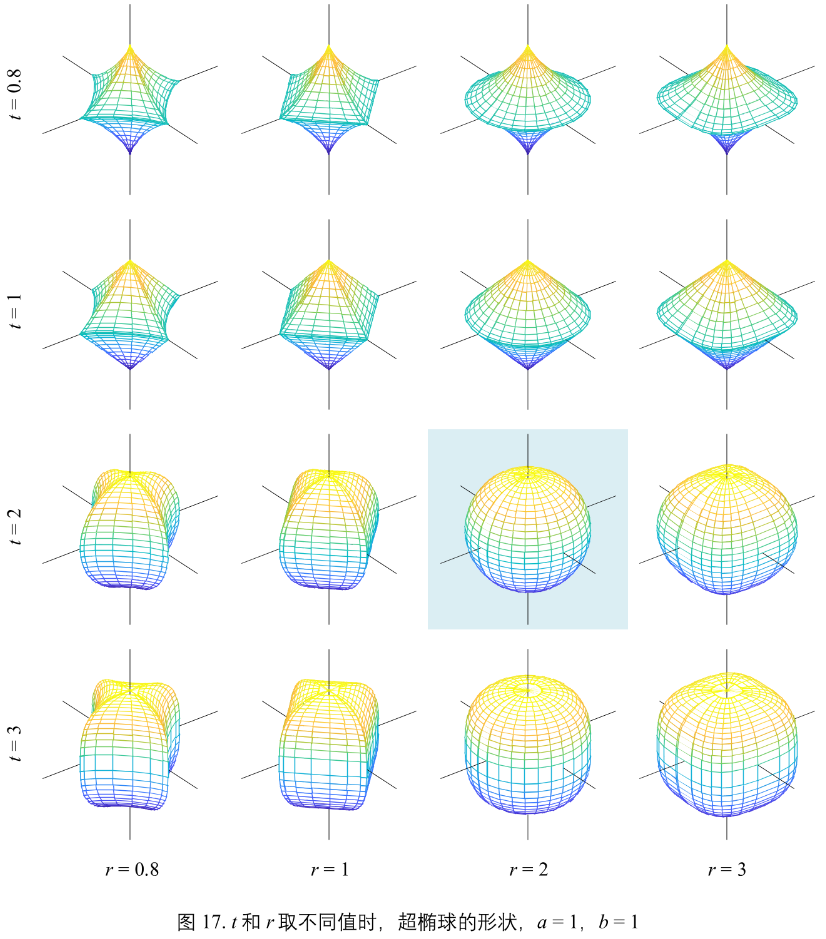
从二维到三维，可以得到超椭球，解析式（20）：$ (\vert \frac{x_{1}}{a}\vert+\vert\frac{x_{2}}{b}\vert)^{\frac{t}{r}} + \vert \frac{x_{3}}{c}\vert^{t} = 1 $
图17 a = 1 和 b = 1，t 和 r 取不同值时，超椭球的形状。

9.6 双曲函数：基于单位双曲线

当 a = 1 和 b = 1 时，为单位双曲线，解析式（23）：$x_{1}^{2} - x_{2}{2} = 1;a, b > 0$
类似前文提到过的三角函数和单位圆之间关系，单位双曲线可以用来定义双曲线函数

图19，最基本的双曲线函数是双曲正弦函数 sinh() 和双曲余弦函数 cosh()

双曲正切 tanh()，通过如下计算得到：$tanh\theta = \frac{sinh\theta}{cosh\theta}$

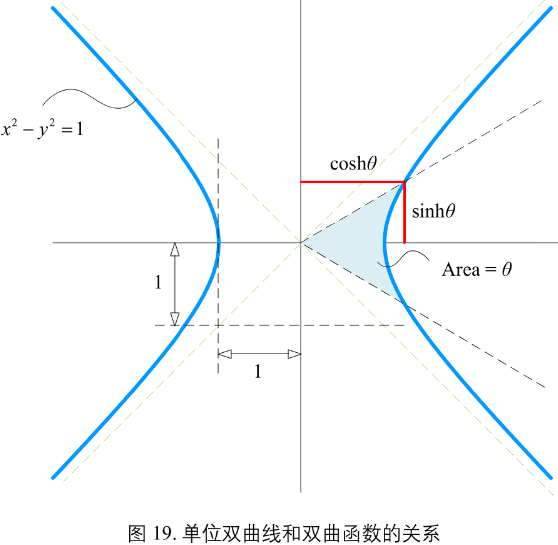
图20，为 $sinh\theta$, $cosh\theta$, $tanh\theta$ 三个函数之间的图像关系

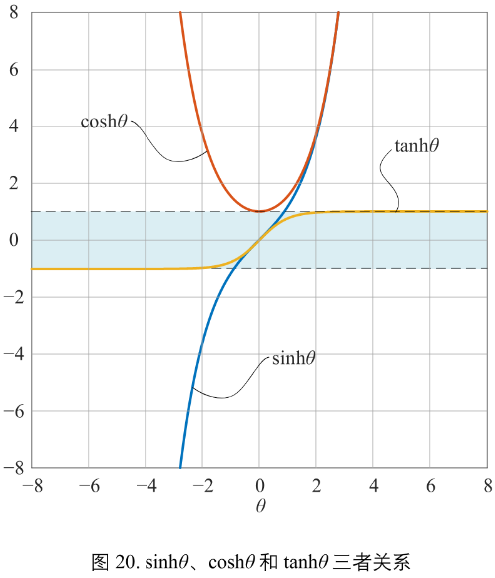
和指数函数关系

$sinh\theta$, $cosh\theta$, $tanh\theta$ 三个函数和指数函数 $\exp(\theta)$ 存在以下关系：
$sinh\theta = \frac{\exp(\theta) - \exp(-\theta)}{2}$

$cosh\theta = \frac{\exp(\theta) + \exp(-\theta)}{2}$

$tanh(\theta) = \frac{sinh\theta}{cosh\theta} = \frac{\exp(\theta)-\exp(-\theta)}{\exp(\theta)+\exp(-\theta)}$
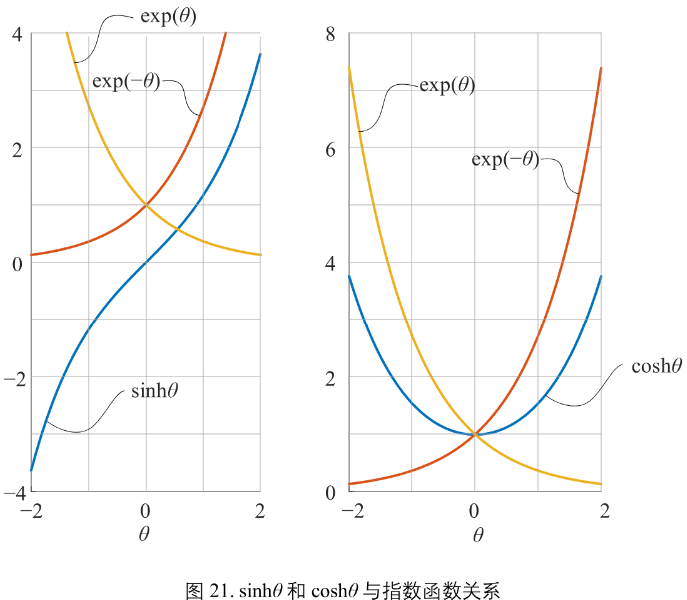
图21：
$sinh\theta$, $cosh\theta$ 与指数函数的关系

9.7 圆锥曲线一般式

解析式（26）：$Ax_{1}^{2} + Bx_{1}x_{2} + Cx_{2}^{2} + Dx_{1} + Ex_{2} + F = 0$

满足$Ax_{1}^{2} + Cx_{2}^{2} + Dx_{1} + Ex_{2} + F = 0, A = C$，圆锥曲线为正圆

满足$Ax_{1}^{2} + Cx_{2}^{2} + Dx_{1} + Ex_{2} + F = 0, A \ne C, AC > 0$，圆锥曲线为正椭圆，即没有旋转

满足$Ax_{1}^{2} + Cx_{2}^{2} + Dx_{1} + Ex_{2} + F = 0, AC < 0$，圆锥曲线为正双曲线

满足下列任一等式，圆锥曲线为正抛物线：
$ \begin{cases} Ax_{1}^{2} + Dx_{1} + Ex_{2} + F = 0\\ Cx_{2}^{2} + Dx_{1} + Ex_{2} + F = 0 \end{cases} $

矩阵运算

$
\frac{1}{2}
\begin{bmatrix}
x_{1} \ x_{2}
\end{bmatrix}^{T}

\begin{bmatrix}
2A & B \
B & 2C
\end{bmatrix}

\begin{bmatrix}
x_{1} \
x_{2}
\end{bmatrix} +

\begin{bmatrix}
D \
E
\end{bmatrix}^{T}

\begin{bmatrix}
x_{1} \
x_{2}
\end{bmatrix} + F = 0
$