鸢尾花书 - Book_3《数学要素》 - Chapter7 距离
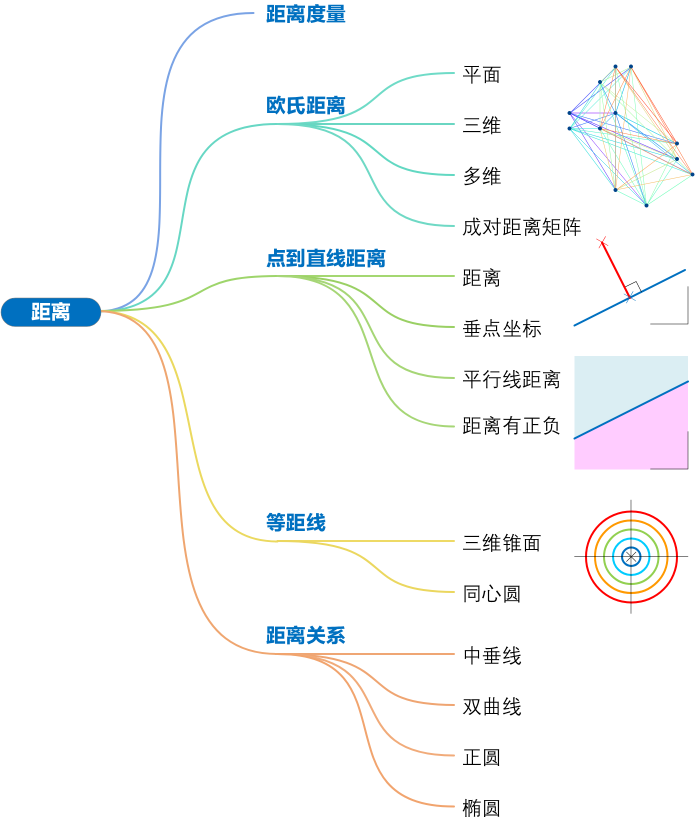
距离:未必是两点间最短线段
计算距离时还可以考虑数据的分布因素,得到的距离是统计距离。
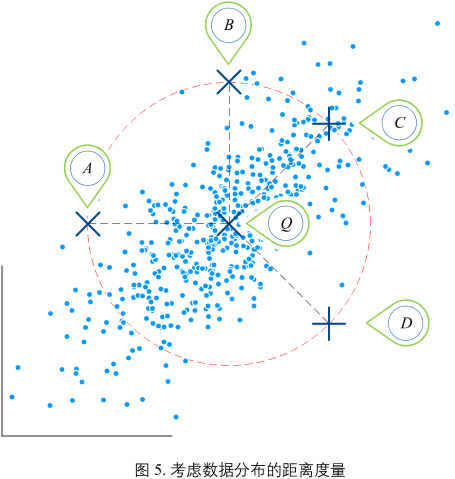
如图5,A B C D 与 Q 点的直线距离相同(欧式距离)。考虑数据分布“紧密”情况,C 点距离 Q 最近,D 最远。地理上相近,不代表关系紧密。
欧式距离:两点间最短线段
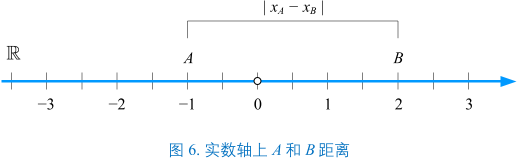
两点之间的线段长度叫做欧几里得距离(欧氏距离)。$\mathrm{dist}(A, B) = \vert x_{A} - x_{B} \vert $
二维平面
计算公式:\(\mathrm{dist}(A, B) = \sqrt{(\vert x_{A} - x_{B} \vert)^{2} - (\vert y_{A} - y_{B} \vert)^{2}}\) 或 \(\sqrt{(x_{A} - x_{B})^{2} + (y_{A} - y_{B})^{2}}\)
利用矩阵乘法:\(\mathrm{dist(A, B)} = \sqrt{\begin{bmatrix}x_{A} - x_{B}&y_{A} - y_{B}\end{bmatrix} \begin{bmatrix} x_{A} - x_{B}\\y_{A} - y_{B} \end{bmatrix}}\)
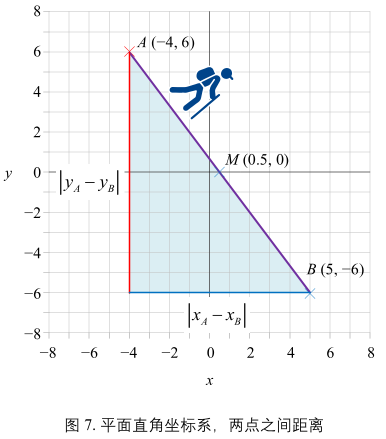
图 7 中 A B 点连线的中点 M 的坐标为:\(M = (\frac{x_{A} + x_{B}}{2}, \frac{y_{A} + y_{B}}{2})\)
三维空间
计算公式:\(\mathrm{dist}(A, B) = \sqrt{(x_{A} - x_{B})^{2} + (y_{A} - y_{B})^{2} + (z_{A} - z_{B})^{2}}\)
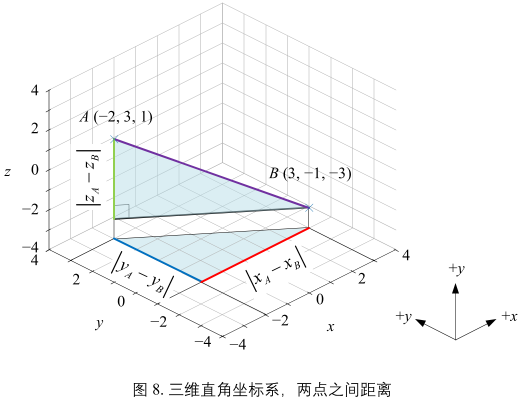
把三维空间计算空间推广到多维:\(\mathrm{dist}(A, B) = \sqrt{(x_{1, A} - x_{1, B})^{2} + (x_{2, A} - x_{2, B})^{2} + \cdots + (x_{D, A} - x_{D, B})^{2}}\)
写成矩阵乘法:\(\mathrm{dist}(A, B) = \sqrt{\begin{bmatrix} x_{1, A} - x_{1, B}&x_{2, A} - x_{2, B}&\cdots x_{D, A} - x_{D, B}\end{bmatrix}\begin{bmatrix}x_{1, A} - x_{1, B}\\x_{2, A} - x_{2, B}\\x_{D, A} - x_{D, B}\end{bmatrix}}\)
成对距离
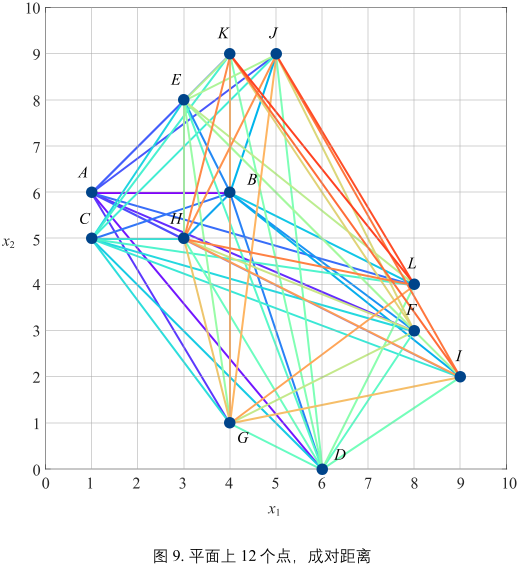
图9 共 12 个点。可构成 \(C_{12}^{2} = 66\) 个两点距离。
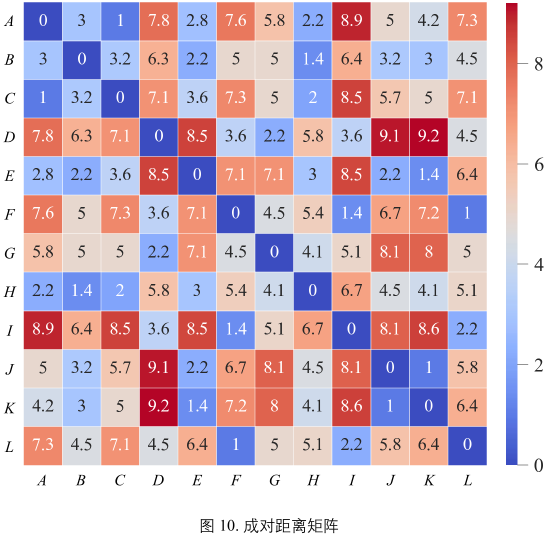
图10 矩阵的形状为 12行,12列。矩阵的主对角线元素都是 0,某点和自身的距离。矩阵非主对角线元素则代表成对距离。
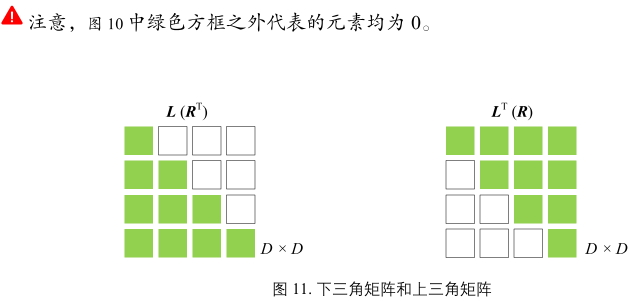
下三角矩阵、上三角矩阵
点到直线的距离
给定平面上一条直线 l,\(ax + by + c = 0\)
给定平面上一点 A(x_{A}, y_{A})
点到该直线的距离:\(\mathrm{dist}(A,l) = \frac{\vert ax_{A} + by_{A} + c \vert}{\sqrt{a^{2} + b^{2}}}\),A 和 H 的连线得到 AH 线段长度。
直线 l 上距离 A 最近点的坐标为 \(H(x_{H}, y_{H})\)
\(x_{H} = \frac{b(bx_{A} - ay_{A}) - ac}{a^{2} + b^{2}}\) ,
\(y_{H} = \frac{a(-bx_{A} + ay_{A}) - bc}{a^{2} + b^{2}}\)
当 a = 0时,直线 l 为水平线。\(A(x_{A}, y_{A})\) 到该直线的距离为:\(\mathrm{dist}(A, l) = \frac{\vert by_{A} + c \vert}{\vert b \vert}\)
当 b = 0时,直线 l 为竖直线。\(A(x_{A}, y_{A})\) 到该直线的距离为:\(\mathrm{dist}(A, l) = \frac{\vert ax_{A} + c \vert}{\vert a \vert}\)
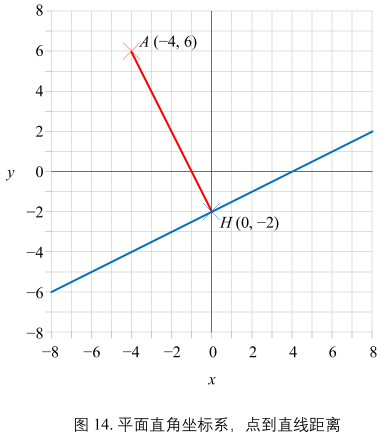
举个例子:图14给定直线 \(x - 2y - 4 = 0\),A(-4, 6) 到直线距离最近点为 H(0, -2), A 到直线的距离为 8.944
平行线间的距离
给定如下两条平行线 \(l_{1}\) 和 \(l_{1}\) 对应的解析式:
\(\begin{cases} ax + by + c_{1} = 0 \\ ax + by + c_{2} = 0 \end{cases}\)
其中,\(c_{1} \neq c_{2}\) 这两条平行线的距离为:\(\mathrm{dist}(l_{1}, l_{2}) = \frac{\vert c_{1} - c_{2} \vert}{\sqrt{a^{2} + b^{2}}}\)
距离也可以有正负
在机器学习算法中,我们经常会给距离度量加个正负号
如图 15 所示,在数轴上,以为 Q 点作为比较的基准点,距离 AQ 和 BQ 的定义分别为:
\(\mathrm{dist}(A, Q) = \vert x_{A} - x_{Q} \vert\)
\(\mathrm{dist}(B, Q) = \vert x_{B} - x_{Q} \vert\)

将上式两个绝对值去掉,得到:
\(\mathrm{dist}(A, Q) = x_{A} - x_{Q}\)
\(\mathrm{dist}(B, Q) = x_{B} - x_{Q}\)
图 15 中,A 在 Q 的左边,因此 \(x_{A} - x_{Q} < 0\),距离为“负”;而 B 在 Q 的右边,因此 x_{B} - x_{Q} > 0,也就是距离为“正”距离的绝对值告诉我们两点的远近,距离的“正负”符号则多了相对位置这层信息。“正负”的距离把不等式“区域”这封信息也囊括了进来。
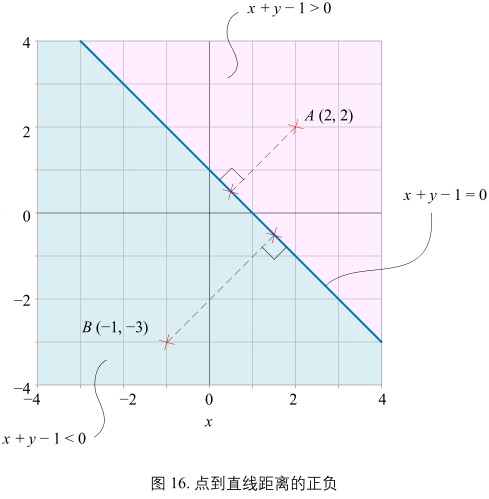
同理,将 \(\mathrm{dist}(A,l) = \frac{\vert ax_{A} + by_{A} + c \vert}{\sqrt{a^{2} + b^{2}}}\) 绝对值符号去掉,点 A 的直线 l 的距离为:\(\mathrm{dist}(A,l) = \frac{ax_{A} + by_{A} + c}{\sqrt{a^{2} + b^{2}}}\),以图16为例,图中直线 l 的解析式为 \(x + y - 1 = 0\);这条直线把平面直角坐标系划分成两个区域:\(x + y - 1 > 0\)(暖色背景) 和 \(x + y - 1 < 0\)(冷色背景)。根据 \(\mathrm{dist}(A,l) = \frac{ax_{A} + by_{A} + c}{\sqrt{a^{2} + b^{2}}}\) 计算 A 和 B 点的直线 l 的含“正负”距离分别为:\(\mathrm{dist}(A, l) = \frac{3}{\sqrt{2}}\), \(\mathrm{B, l} = \frac{-5}{\sqrt{2}}\)
等距线:换个视角看距离
任意一点 \(P(x, y)\) 距原点 \(O(0, 0)\) 的欧式距离 r,对应的解析式为:\(\mathrm{dist}(P, O) = \sqrt{x^{2} + y^{2} = r}\)
上式左右两侧平方得到:\(x^{2} + y^{2} = r^{2}\),这样我们得到一个圆心位于原点、半径为 r 的正圆的解析式,利用矩阵乘法,可以写成:\(\begin{bmatrix} x&y \end{bmatrix}\begin{bmatrix} x\\y \end{bmatrix} = r^{2}\),构造二元函数:\(f(x, y) = \sqrt{x^{2} + y^{2}}\),其中 x 和 y 为自变量。
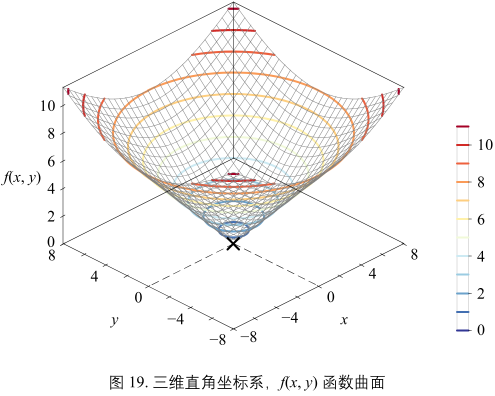
图19 所示为 f(x, y) 在三维直角坐标系的曲面形状,这个曲面显然为圆锥。
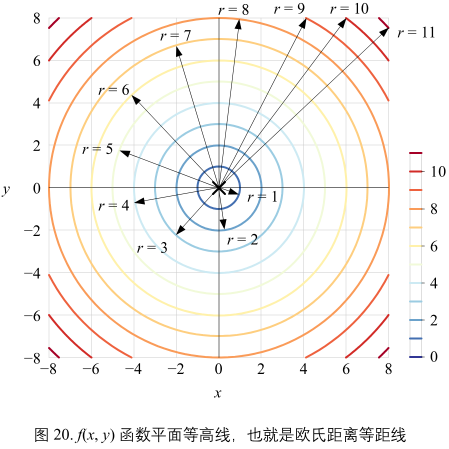
将图19 等高线投影到 xy 平面上,便得到如图 20 所示的平面等高线,我们管它叫等距线。图20 中每条等距线对应的就是 \(f(x, y) = r\) 截面图像。观察图19,很容易发现 r 取不同值时对应一系列同心圆。也就是说,距离原点 O 的欧式距离取不同值时,等距线是一系列同心圆。
距离间的量化关系
中垂线
线段 AP 和 BP 等距
得到的是 A 和 B 两点的中垂线:\(AP = BP\)
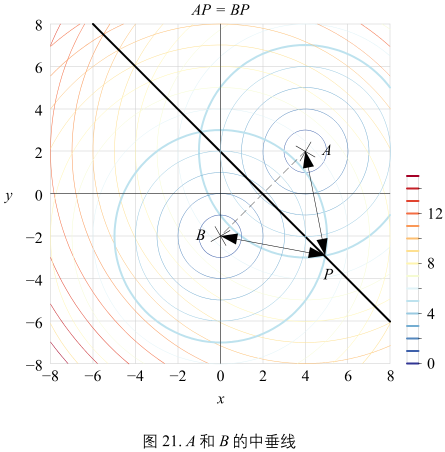
如图21 所示,A 和 B 两点的中垂线垂直于 AB 线段,并且将 AB 等分;图21两组等高线,对应的是到 A 和 B 两点等距线,相同颜色代表相同距离。相同颜色等距线的交点显然都在中垂线上。
双曲线
线段 AP 和 BP 差为定值
\(AP - BP = c\),比如,AP 比 BP 长 3,即:\(AP - BP = 3\)
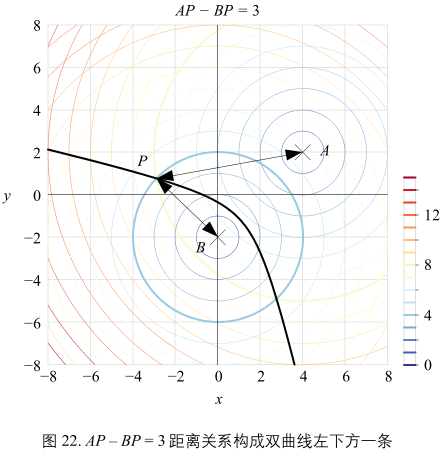
如图22所示,我们满足上述公式数值关系的 P 构成了一条双曲线。双曲线等圆锥曲线。
将 \(AP - BP = 3\) 变成 \(AP - BP = -3\),也就是 AP 比 BP 短3。
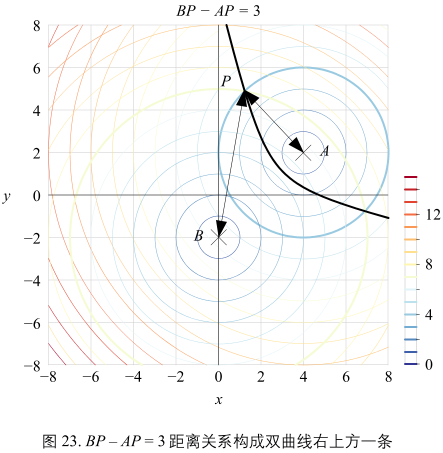
图23给出了对应的图像,这时 P 的轨迹是双曲线右上方那一条。
注:图22和图23构成一对完成的双曲线。
正圆
线段 AP 和 BP 满足倍数关系
\(AP = c \dot BP\),举例:\(AP = 2BP\)
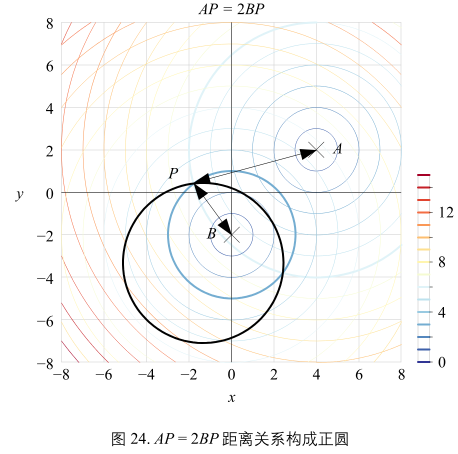
如图24,P 轨迹对应的是正圆。
椭圆
线段 AP 和 BP 之和为定值
\(AP + BP = c\),举例:\(AP + BP = 8\)
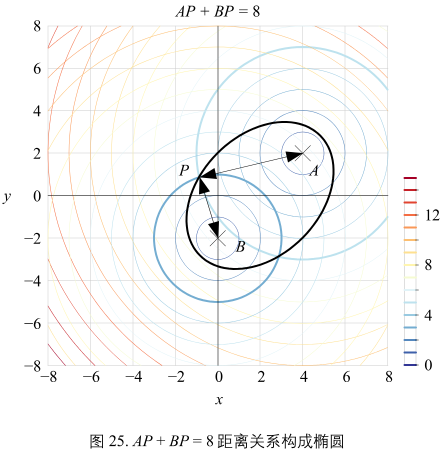
图25,P 的轨迹是一个椭圆。
注:以上内容均摘自生姜博士的鸢尾花书系列-Book_3《数学要素》




 浙公网安备 33010602011771号
浙公网安备 33010602011771号