鸢尾花书 - Book_3《数学要素》 - Chapter6 三维坐标系

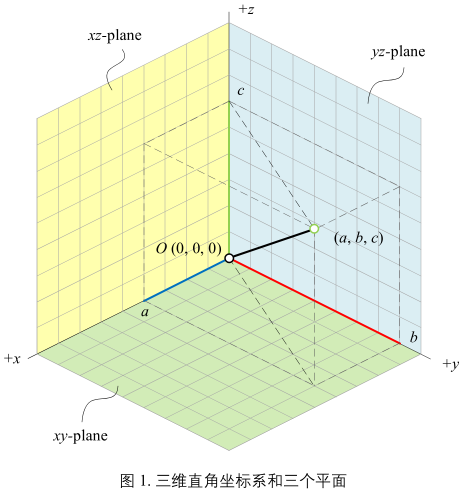
三维直角坐标系

x 轴（横轴）、y 轴（纵轴）、z 轴（竖轴）

xy 平面

x 轴和 y 轴构成 xy 平面。z 轴垂直于 xy 平面

yz 平面

y 轴和 z 轴构成 yz 平面。x 轴垂直于 yz 平面

xz 平面

x 轴和 z 轴构成 xz 平面。y 轴垂直于 xz 平面

这三个平面将三维空间分成 8 个部分，成为卦限。

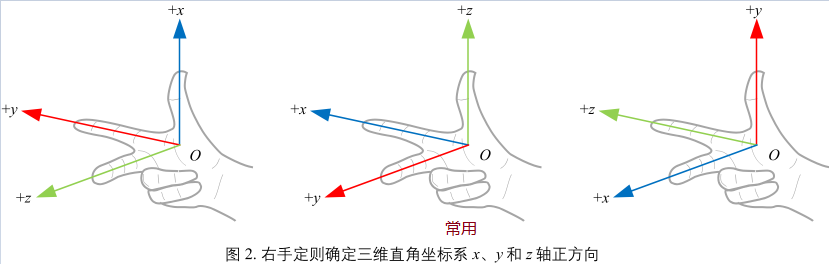
空间平面：三元一次方程

\(ax + by + cz + d = 0\) 其中 x y z 为变量，a b c d 为参数。实际上这个方程就是三元一次方程。利用矩阵乘法可以写成：\(\begin{bmatrix}a&b&c\end{bmatrix}\begin{bmatrix}x\\y\\z\end{bmatrix} + d = 0\)

第一个平面

解析式：\(x + y - z = 0\)
网格面的颜色对应 z 的数。 z 越大，越靠近暖色系；z 越小，越靠近冷色系。

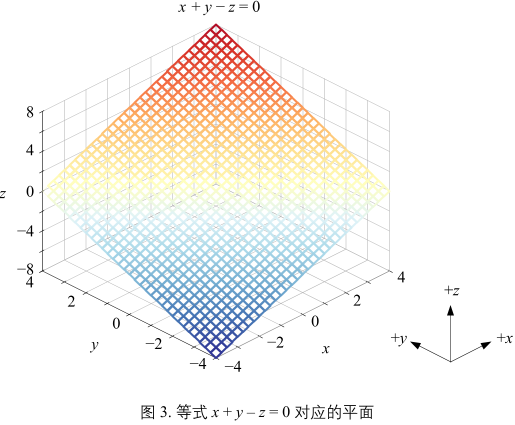
以 z 作为因变量、x 和 y 作为自变量的话，\(x + y - z = 0\) 等价于 \(z = f(x, y) = x + y\)

第二个平面

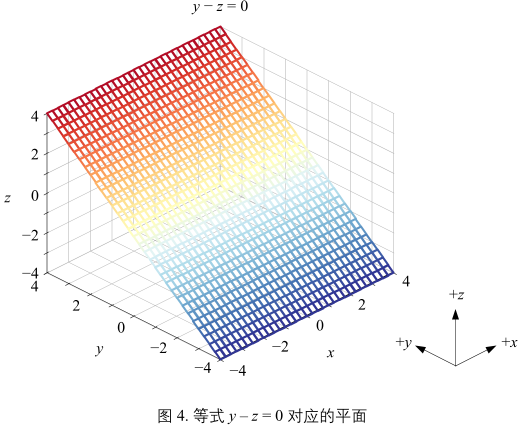
解析式：\(y - z = 0\)
图4中网格面平行于 x 轴，垂直于 yz 平面。不管 x 取任何值，图4平面上的点 y 和 z 的关系都满足 \(y - z = 0\)

第三个平面

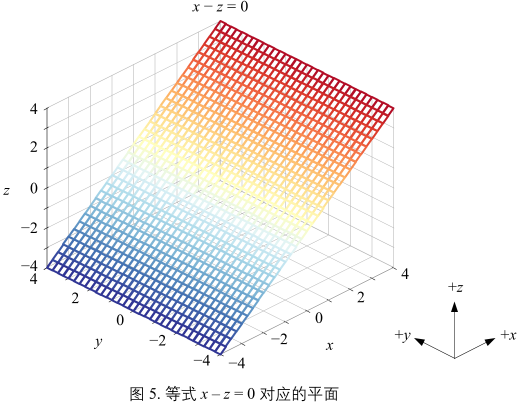
解析式：\(x - z = 0\)
图5中网格面平行于 y 轴，垂直于 xz 平面。不管 y 取任何值，图5平面上的点 y 和 z 的关系都满足 \(x - z = 0\)

第四个平面

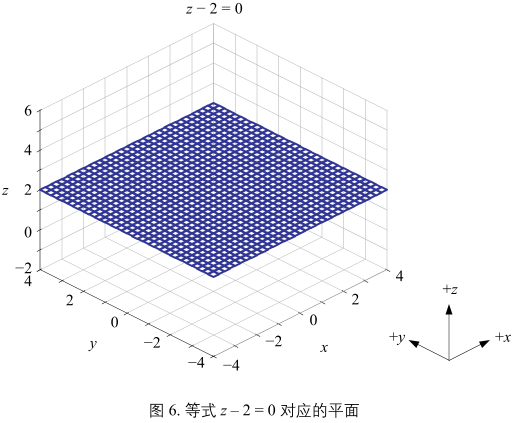
解析式：\(z - 2 = 0\)
图6中网格面平行于 xy 面，垂直于 z 轴。从函数角度，这个平面可以看作是二元常数含量，写成：\(f(x, y) = c\)

最后三个平面

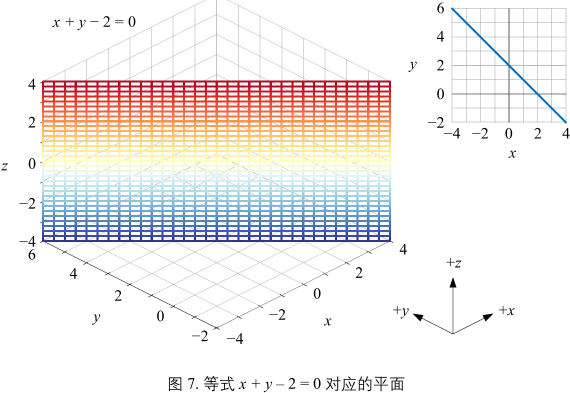
解析式：\(x + y - 2 = 0\)

解析式：\(x + 2 = 0\)

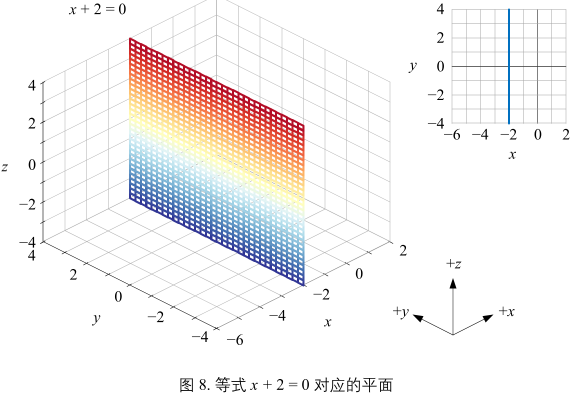
解析式：\(y - 2 = 0\)

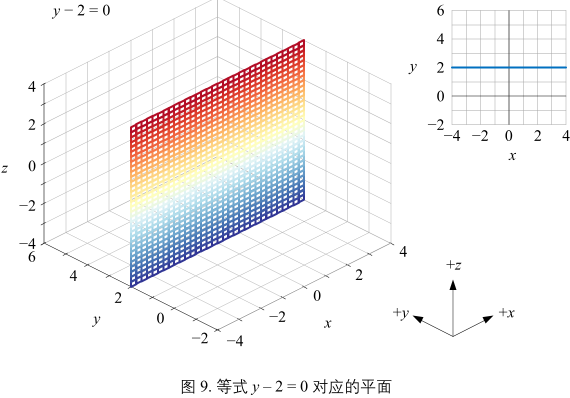
图7~9有一个共同特点，都垂直于 xy 平面。z 的取值不影响平面和 xy 平面的相对位置。三个平面都相当于 xy 平面上一条直线沿 z 方向展开。反过来看，图7~9 平面在 xy 平面上的投影为一条直线

线性

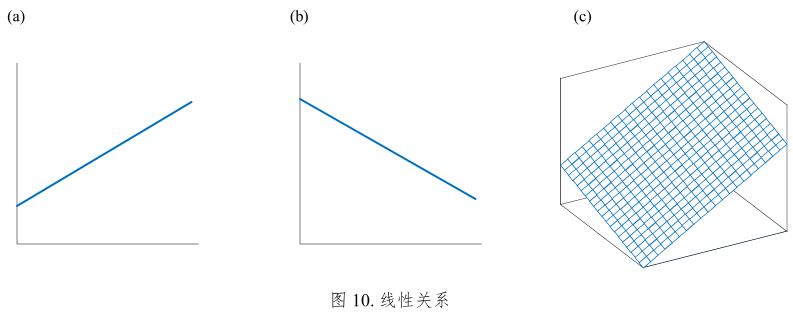
1. 变量之间的关系可以用一条斜线表示，比如 \(y = ax + b\)。平面上，线性函数即一次函数，对应图像为一条斜线。
2. 三维直角坐标系中，“线性”对应几何形式是斜面，也就是二元一次函数，比如 \(y = b_{1}x_{1} + b_{2}x_{2} + b_{0}\)
3. 对于多元函数，线性的形式为 \(y = b_{1}x_{1} + b_{2}x_{2} + b_{3}x_{3} + \cdots + b_{n}x_{n} + b_{0}\)
   图10给出线性关系三个例子：
   

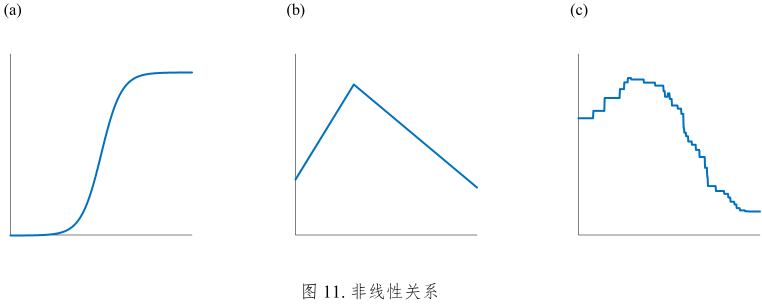
非线性

对应的图像不是直线、也不是平面、更不是超平面。平面上，非线性关系可以是曲线、折线、甚至不能用参数来描述。这种不能用参数描述的情况在数学上叫非参数。

监督学习

回归模型：研究变量和自变量之间的关系，目的是分析预测。

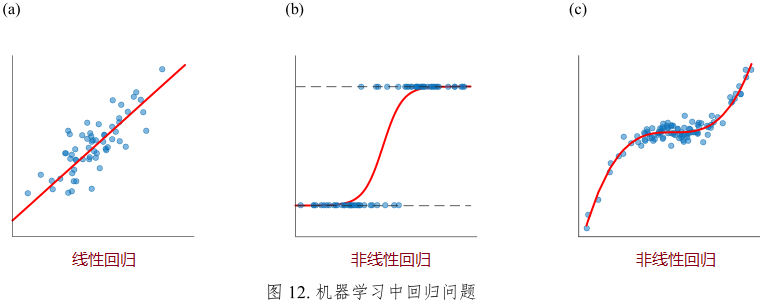
二分类模型：分割不同标签数据点的边界线叫决策边界

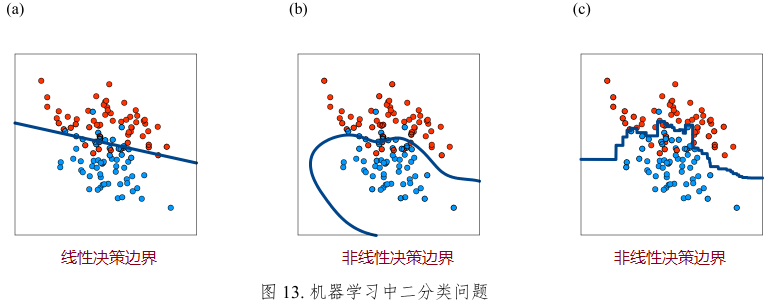
空间直线：三元一次方程组

两个平面相交便确定一条空间直线。也就是说，多数情况下，两个三元一次方程确定一条三维空间直线。

两个平面相交一点

\(\begin{cases} x + y - z = 0\\ 2x - y - z = 0 \end{cases}\)
上式中，每个方程代表三维空间的一个平面。如图14所示，这两个平面相交得到一条直线。

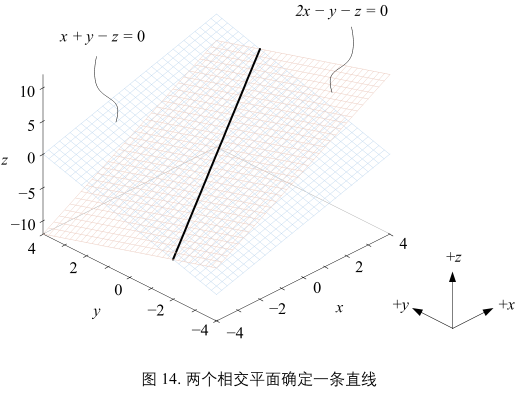
从代数角度，这两个三元一次方程构成的方程组有无数组解，这些解都在图14所示的黑色直线上。

三个平面相交一点

\(\begin{cases} x + y - z = 0\\ 2x - y - z = 0\\ -x + 2y - z + 2 = 0 \end{cases}\)

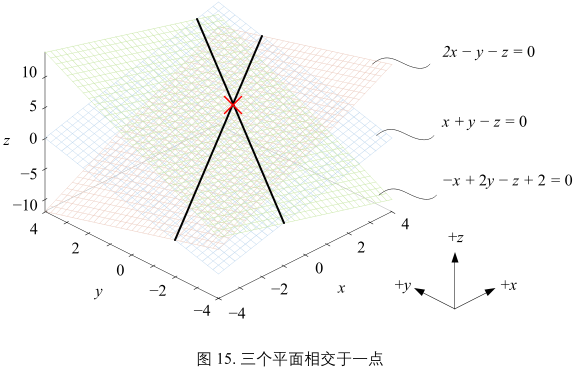
三个平面相交于一点，这个三元一次方程组有唯一解。

三个平面相交一点的矩阵形式

\(\begin{bmatrix}1&1&-1\\2&-1&-1\\-1&2&1\end{bmatrix} \begin{bmatrix}x\\y\\z\end{bmatrix} = \begin{bmatrix}0\\0\\-2\end{bmatrix}\)
这种形式叫做线性方程组，一般写成 \(Ax = b\)。当线性方程数有很多时，\(Ax = b\) 这种形式更规整，更便于计算。对矩阵 A 和增广矩阵 [A b] 各种性质研究，可以判定线性方程组解的特点。

三元一次方程组解的个数

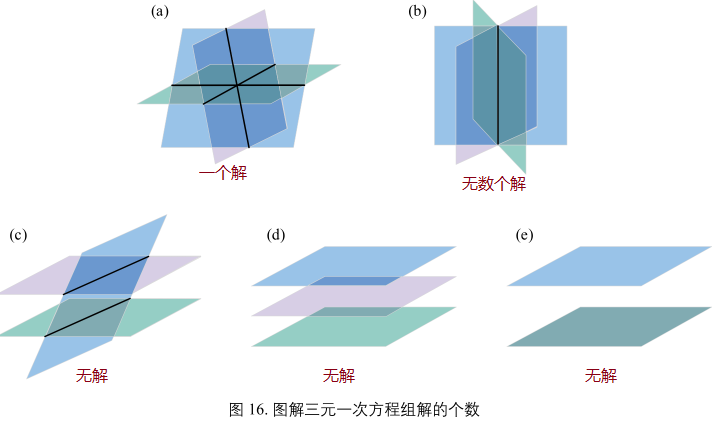
不等式：划定区域

等式

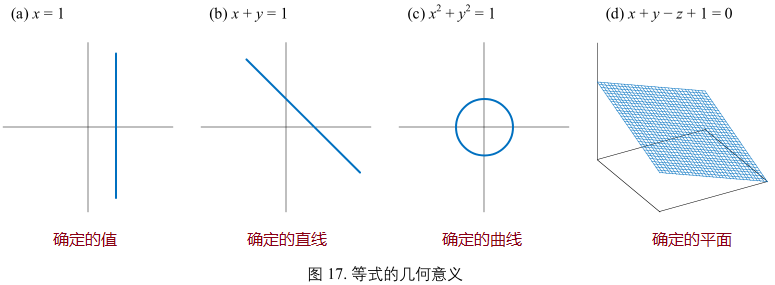
不等式

不等式的几何意义则是划定区域

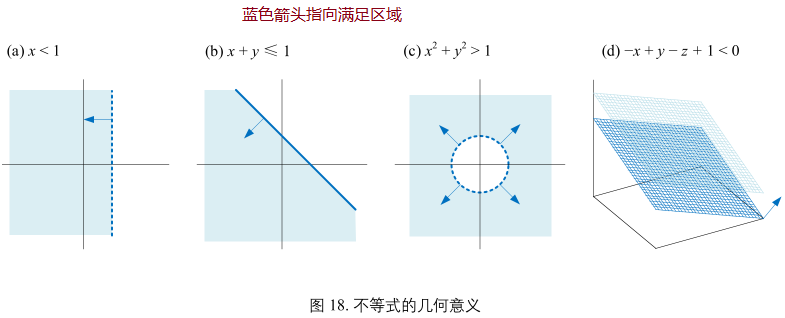
图17和图18为几何视角，是理解代数式最直接的方式。

数轴、绝对值、大小

数轴：每一个点对应一个实数，原点右侧为正数、原点左侧为负数。
绝对值：数轴上该点于原点的举例。
大小：数轴右边的数大于左边的数

区间

开区间：不包括区间左右端点，记作(a, b)
闭区间：包括区间左右端点，记作[a, b]
左开右闭：(a, b]
左闭右开：[a, b)

优化问题中，如果变量两端均有界，一般只考虑闭区间，即可以取到区间端点数值。图中a b c d 4 个问题在优化问题中是等价的。 a 叫做下界，b 叫做上界。构造优化问题时，一般都将各种不等式符号调整为\(a \leq b\)。

三大类不等式：约束条件

本节介绍不等式的目的是服务优化问题求解，优化问题中不等式一般分为三大类：

1. 上下界，比如 \(x > 2\)
2. 线性不等式，比如 \(x + y \leq 1\)
3. 非线性不等式，比如 \(x^{2} + y^{2} \geq 1\)
   在优化问题中，这些不等式统称为约束，即限制变量取值范围。

上下界

1. 给定 \(x_{1}\) 的取值范围为：\(x_{1} + 1 > 0\)
2. 将式子 \(>\) 调整为 \(<\)，\(-x_{1} - 1 < 0\)
3. 构造二元函数\(f(x1, x2)\)：\(f(x_{1}, x_{2}) = -x_{1} - 1\)

等高线代表函数值相等的点连成的线，即满足 \(f(x_{1}, x_{2} = c)\)

线性不等式

也就是一次不等式，不等式中单项式变量最高次数为 1。可以含有若干未知量。在构造优化问题时，我们还是将两类不等式分开处理。

例1：

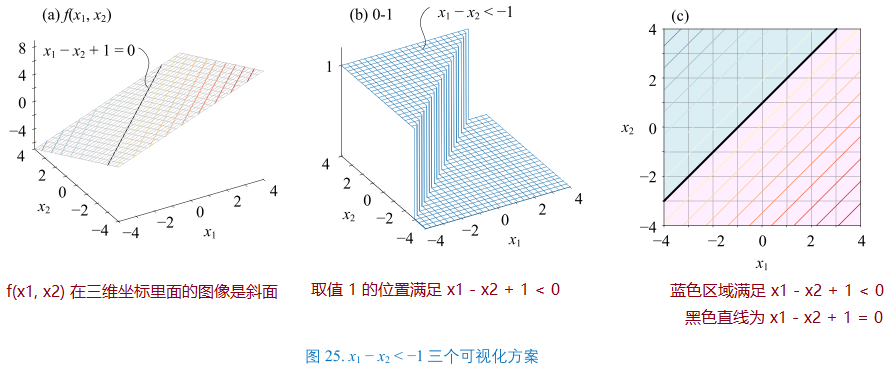
1. 线性不等式：\(x_{1} - x_{2} < -1\)
2. 整理：\(x_{1} - x_{2} + 1 < 0\)
3. 构造二元函数：\(f(x_{1}, x_{2}) = x_{1} - x_{2} + 1\)
   

例2：

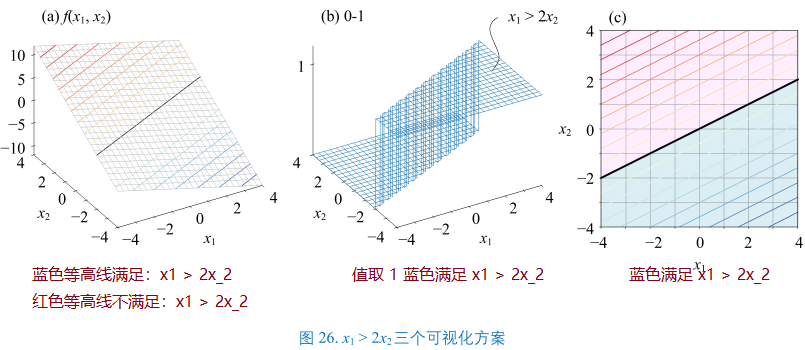
1. 线性不等式：\(x_{1} > 2x_{2}\)
2. 整理：\(-x_{1} + 2x_{2} < 0\)
3. 构造二元函数：\(f(x_{1}, x_{2}) = -x_{1} + 2x_{2}\)
   

非线性不等式

例1：

1. 非线性不等式：\(|x_{1} + x_{2}| < 1\) 等价：\((x_{1} + x_{2})^{2} < 1\)
2. 整理：\(|x_{1} + x_{2}| - 1 < 0\)
3. 构造二元函数：\(f(x_{1}, x_{2}) = |x_{1} + x_{2}| - 1\)

例2：

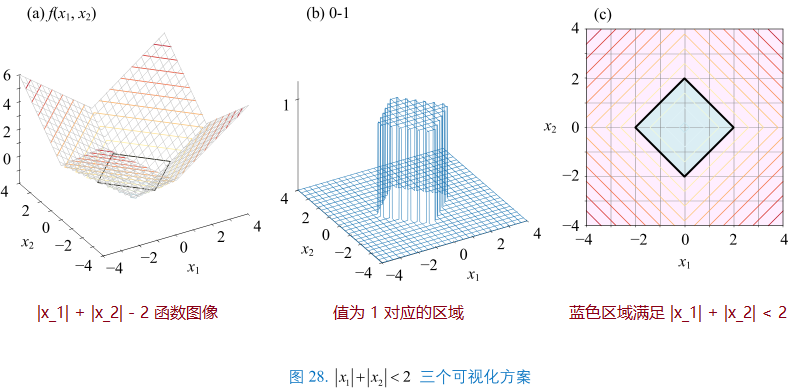
1. 非线性不等式：\(|x_{1}| + |x_{2}| < 2\)
2. 整理：\(|x_{1}| + |x_{2}| - 2 < 0\)
3. 构造二元函数：\(f(x_{1}, x_{2}) = |x_{1}| + |x_{2}| - 2\)
   

例子3：

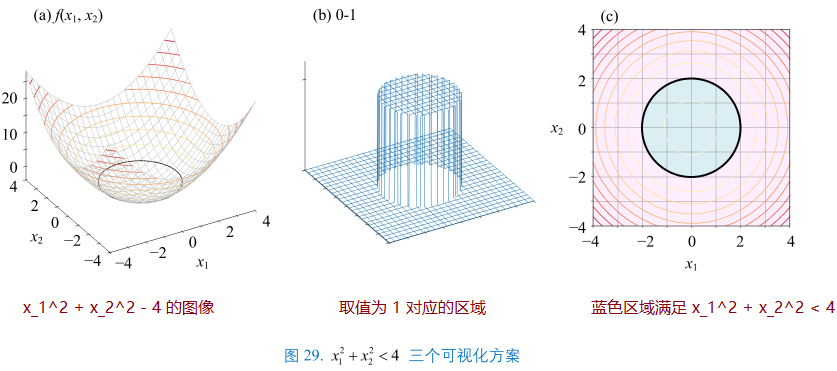
1. 非线性不等式：\(x_{1}^{2} + x_{2}^{2} < 4\) 等价：\(\sqrt{x_{1}^{2} + x_{2}^{2}} < 2\)
2. 整理：\(x_{1}^{2} + x_{2}^{2} - 4 < 0\)
3. 构造二元函数：\(f(x_{1}, x_{2}) = x_{1}^{2} + x_{2}^{2} - 4\)
   

注：以上内容均摘自生姜博士的鸢尾花书系列-Book_3《数学要素》