鸢尾花书 - Book_3《数学要素》 - Chapter5 笛卡尔坐标系
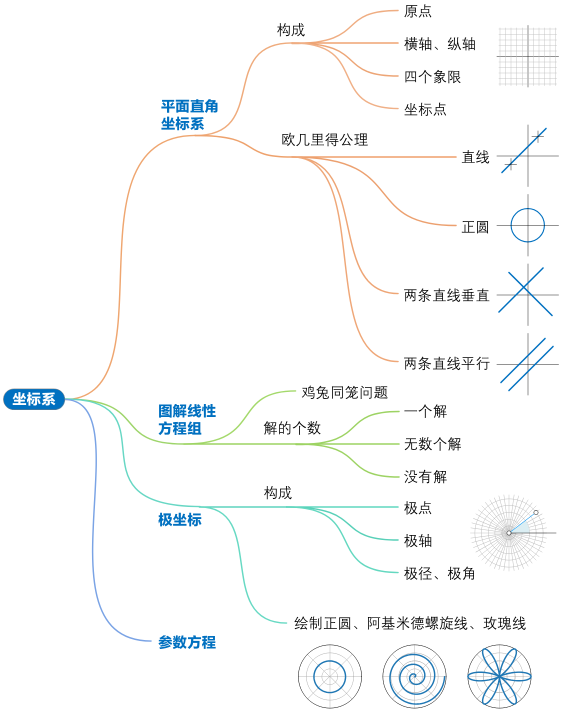
平面直角坐标系(笛卡尔坐标系)
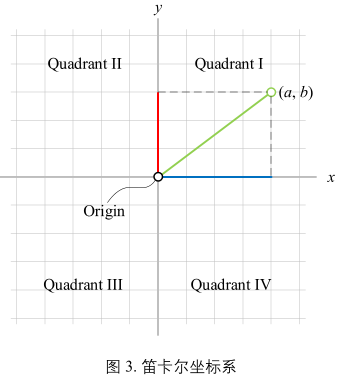
两个相交于原点相互垂直的实数轴。横轴 x 轴;纵轴 y 轴。
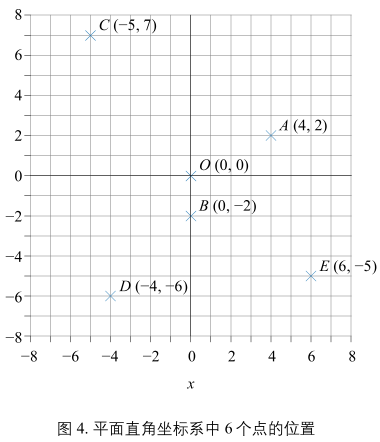
直线
任意两点可以画一条直线,这条直线一般对应代数中的二元一次方程。\(ax + by + c = 0\)。使用矩阵乘法可以写成:\(\begin{bmatrix}a&b\end{bmatrix}\begin{bmatrix}x\\y\end{bmatrix} + c = 0\)
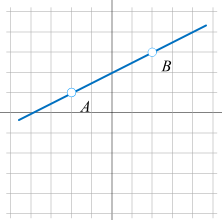
\(ax + by + c = 0\) 当 a = 0,直线平行于横轴。可以写成 \(by + c = 0\)
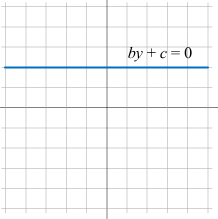
\(ax + by + c = 0\) 当 b = 0,直线平行于纵轴。可以写成 \(ax + c = 0\)
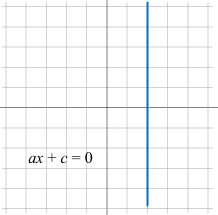
\(ax + by + c = 0\) 如果 a、b 均不为 0。可以写成 \(y = -\frac{a}{b}x-\frac{c}{b}\),过程如下:
- \(ax + by + c = 0\)
- \(by = -ax - c\)
- \(y = -\frac{ax}{b} - \frac{c}{b}\)
- \(y = -\frac{a}{b}x - \frac{c}{b}\)
当 x 为自变量、y 为因变量时,实际上就变成了一元一次函数。其中 \(-\frac{a}{b}\) 为直线斜率,\(-\frac{c}{b}\)为纵轴截距
两点距离
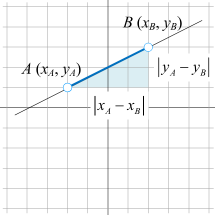
\(AB = \sqrt{(x_{A} - x_{B})^{2} + (y_{A} - y_{B})^2}\)
正圆
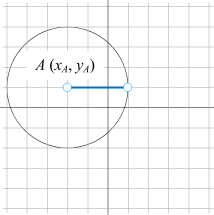
以 \(A(x_{A}, y_{A})\) 点为圆心,r 为半径画一个圆。圆上任意一点 \(x(x, y)\) 到 \(A(x_{A}, y_{A})\) 点的距离 r
\(\sqrt{(x - x_{A})^2 + (y - y_{A})^2} = r\)
两边平方得到上图解析式:
\((x - x_{A})^2 + (y - y_{A})^2 = r^{2}\)
使用矩阵乘法,可以写成: \(\begin{bmatrix}x-x_{A}&y-y_{A}\end{bmatrix}\begin{bmatrix}x-x_{A}\\y-y_{A}\end{bmatrix} - r^{2} = 0\)
特别地,当圆心为远点\((0, 0)\),半径 r = 1时,圆的单位圆,对应解析式为:
\(x^{2} + y^{2} = 1\)
使用矩阵乘法,可以写成:\(\begin{bmatrix}x&y\end{bmatrix}\begin{bmatrix}x\\y\end{bmatrix} - 1 = 0\)
垂直
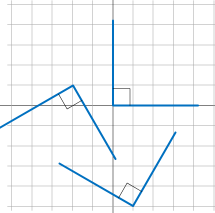
判断 \(ax + by + c = 0\) 和 \(ax + \beta + \gamma = 0\) 是否垂直
\(a\alpha + b\beta = 0\)
如果系数a、b、a、\(\beta\) 均不为 0 时,两条线直线垂直,则两条线直线斜率相乘为 -1
\(\frac{a}{b}\frac{\alpha}{\beta} = -1\)
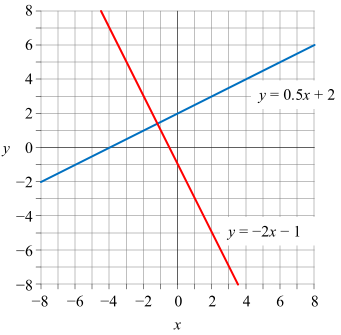
上图分别是 \(y = 0.5x + 2\) 和 \(y = -2x - 1\) 这两个一次函数,相乘斜率为 -1 = 0.5 * (-2)
平行
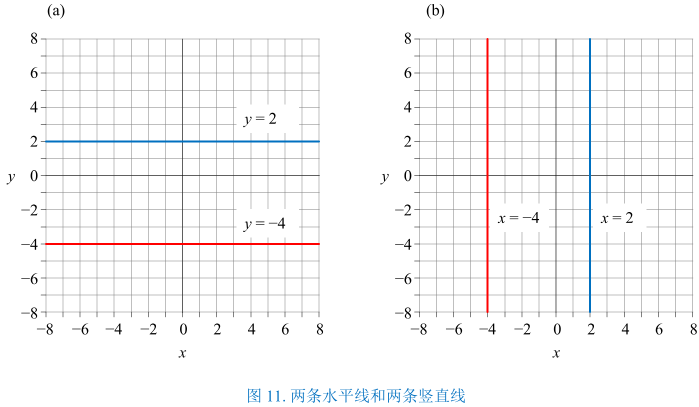
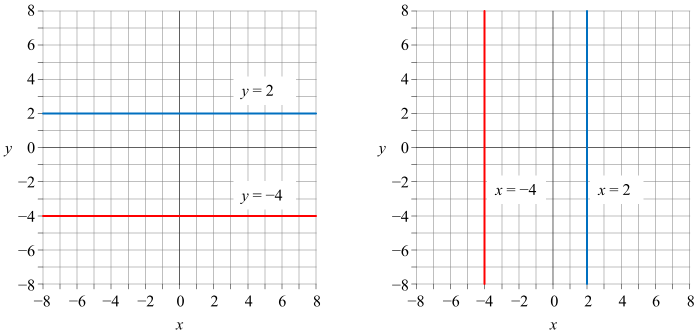
判断 \(ax + by + c = 0\) 和 \(ax + \beta y + \gamma = 0\) 两条直线平行,系数满足:
\(a\beta - b \alpha = 0\)
如果系数 a、b、\(\alpha\)、\(\beta\) 均不为 0 时,两条直线若平行或重合,则两个斜率相同,即:
\(\frac{a}{b} = \frac{\alpha}{\beta}\)
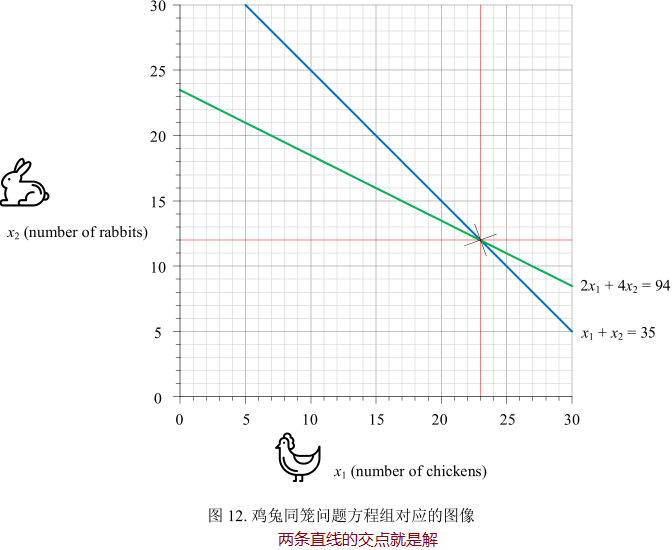
图解“鸡兔同笼”问题
\(\begin{cases}
x_{1} + x_{2} = 35\\
2x_{1} + 4x_{2} = 94
\end{cases}\)
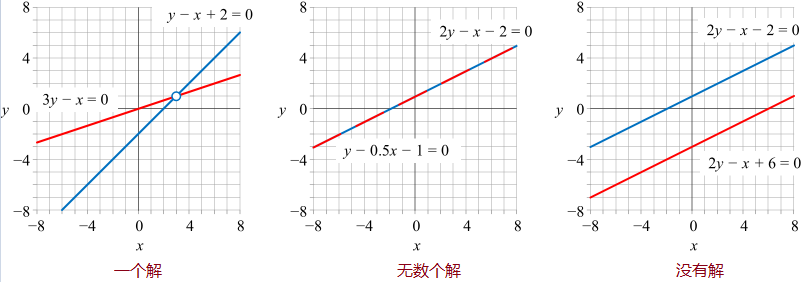
二元一次方程组解的个数
两个二元一次方程构成的方程组可以有一个解、无数解或者没有解
极坐标
极坐标系
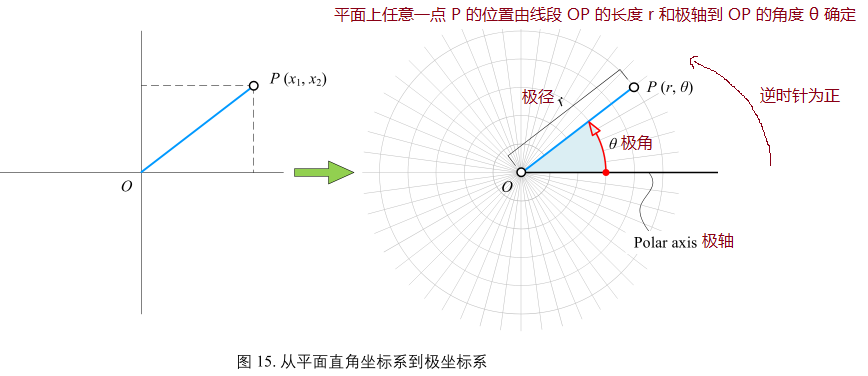
\(\begin{cases}
x_1 = r\cdot\cos\theta\\
x_2 = r\cdot\sin\theta
\end{cases}\)
参数方程:引入一个参数
对于参数任何取值,方程组确定的点 \((x_{1}, x_{2})\) 都在这条曲线上,那么这个方程就叫做曲线的参数方程。
\(\begin{cases}
x_{1} = f(t)\\
x_{2} = g(t)
\end{cases}\)
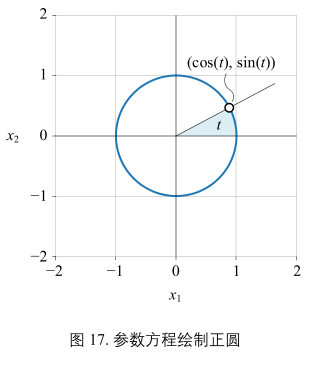
上图公式:
\(\begin{cases}
x_{1} = cos(t)\\
x_{2} = sin(t)
\end{cases}\)
注:以上内容均摘自生姜博士的鸢尾花书系列-Book_3《数学要素》




 浙公网安备 33010602011771号
浙公网安备 33010602011771号