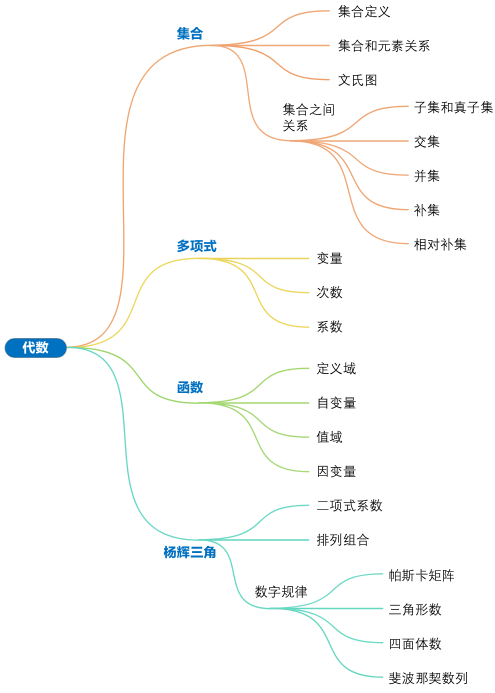
鸢尾花书 - Book_3《数学要素》 - Chapter4 代数

集合与元素

两种关系

属于（belong to）

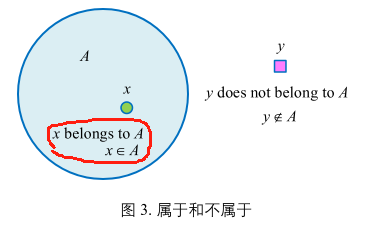
不属于（not belong to）

集合与集合

子集

如果集合 A 中的每一个元素也都是集合 B 中的元素，那么 A 是 B 的子集。记作 \(A \subseteq B\)
举例：集合 B {1, 2}，子集 A 可以是 {1}, {2}, {1,2}

真子集

如果同时满足 \(A \subseteq B\) 并且 \(A \not \equiv B\)，那么 A 是 B 的真子集。记作 \(A \subset B\)
举例：集合 B {1, 2}，真子集 A 是{1}, {2}

交集

同时属于 A 且同时属于 B的元素构成的集合。记作 \(A \bigcap B\)

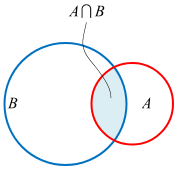
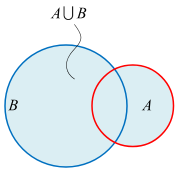
并集

A 集合 和 B 集合合并的集合。记作 \(A \bigcup B\)

相对补集

所有属于 A 但不属于 B 的集合。记作 A - B

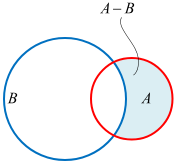
运算举例

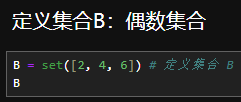
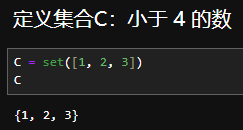
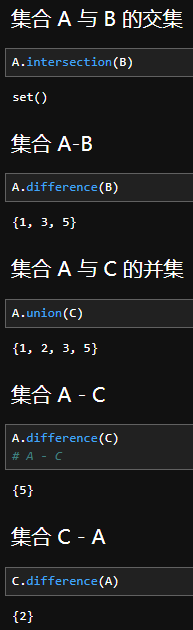
多项式（polynomial）

\(a_{n}x^{n}+a_{n - 1}x^{n - 1}+\cdots + a_{1}x + a_{0}\)

x 为变量（variable），n 为多项式次数（degree of a polynomial），a0、a1....为系数（coefficient）

单项式

由数和字母的积组成的代数式叫做单项式，比如\(a_{n}x^{n}\)。单独的一个数或一个系数也叫单项式，如：5 和 \(a_0\)。一个单项式中，所有变量指数之和，叫做这个单项式的次数。比如 \(3x^{5}\) 的次数是5，\(2xy\) 的次数是2。

多项式

由多个单项式加减构成，比如 \(x+y+8\)、\(x1+x2+8\)

函数

1. 作用

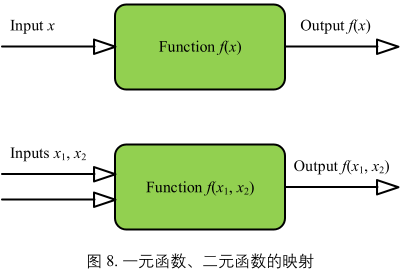
将输入参数通过某种映射规则输出一些结果

2. 函数三要素

定义域 X、值域 y、自变量 x、因变量 y

杨辉三角

二项式系数

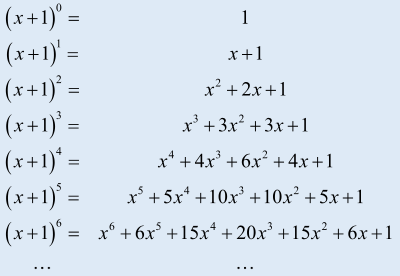
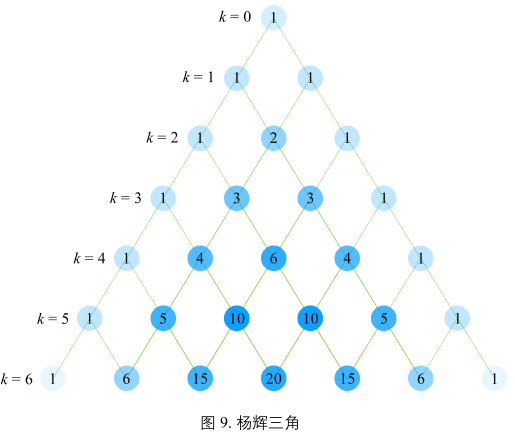
规律

1. 三角形系数呈现对称性，第 k 行有 k + 1 个系数；
2. 三角形每一行左右最外侧系数为 1；
3. 除最外两侧系数以外，三角形内部任意系数为左上方和右上方两个系数之和；
4. 第 k 行系数之和为 \(2^k\)

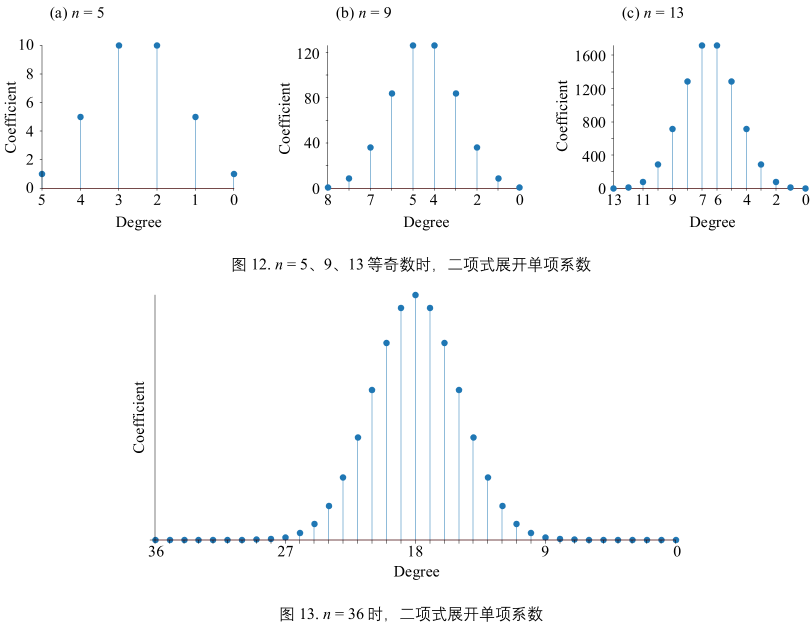
火柴梗图

1. 可视化杨辉三角每行单项式系数的规律。
2. 火柴梗图呈中心对称性。n 为偶数时，对称轴处系数最大。n 为奇数时，对称轴附近两个系数为最大值。对称轴左右两侧系数先快速减小，再慢速减小。
3. 随着 n 增大，会转换成高斯函数（Gaussian function）
   

组合数

1. 从 n 个不同元素中，取 \(m(m \leq n)\) 个元素构成一组，被称作从 n 个不同元素中取出 m 个元素的一个组合（combination），组内元素排序并不重要。
2. n 个不同元素中取出 m 个元素的所有组合个数叫做组合数常记作 \(C_{n}^{m}\)，公式: \(C_{n}^{m}=C(n, m)=\frac{n!}{(n-m)!m!}\)

举例：
从 A B C 三个元素无放回抽取两个，只要元素相同，不管次序是否相同都算作相同结果。结果有 AB、AC、BC，对应组合数：\(C_{3}^{2}=\frac{3!}{(3-2)!2!}=\frac{6}{2}=3\)

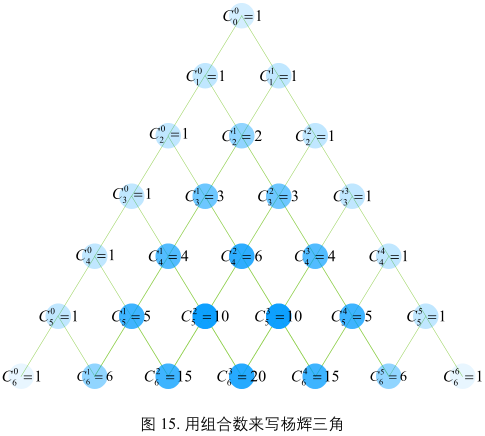
组合数表达杨辉三角

\((x + y)^n = C_{n}^{0}x^{n}y^{0}+C_{n}^{1}x^{n - 1}y^{1}+C_{n}^{2}x^{n - 2}y^{2}+\cdots + C_{n}^{n - 2}x^{2}y^{n - 2}+C_{n}^{n - 1}x^{1}y^{n - 1}+C_{n}^{n}x^{0}y^{n}\)

排列数

1. 从 n 个不同元素中，先后取 \(m(m \leq n)\) 个元素排成一列，叫做从 n 个元素中取出 m 个元素的一个排列，元素排序很重要。
2. n 个不同元素中取出 m 个元素的所有排列的个数叫做排列数，常记作 \(P_{n}^{m}\), \(P_{n}^{m}=\frac{n!}{(n-m)!}\)

举例：
从 A、B、C 三个元素无放回先后抽取两个，结果有 6 个排列 AB、BA、AC、CA、BC、CB，即 \(P_{3}^{2}=\frac{3!}{(3-2)!}=6\)

组合数和排列数

比较组合和排列关系 \(P_{n}^{m}=C_{n}^{m}\cdot m!\)

1. 先从 n 个元素取 m 进行组合 \(C_{n}^{m}\)
2. 把 m 个元素全部排列一边，排列数 \(m!\)
3. \(C_{n}^{m}\cdot m!\) 则是 n 个元素取出 m 的排列数

斐波那契数和杨辉三角

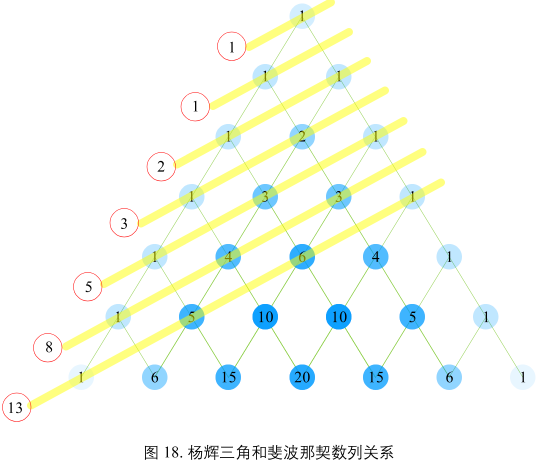
方程

方程（equation）就是含有未知量的等式，比如 x + 5 = 8。使等式成立的未知量的值叫做方程的根（root）或解（solution）

一元一次方程（linear equation in one variable）
\(ax + b = c\) 其中 x 为未知变量，a、b、c为实数，且 \(a \leq 0\)

二元一次方式（linear equation in two variables）
\(ax + by = c\) 其中x, y 为未知变量，a、b、c为实数，且 \(a \not \equiv 0\) \(b \not \equiv 0\)

方程组

指两个或两个以上的方程，一般也会对应两个或两个以上未知量。
\( \begin{cases} x + y = 35 \\ 2x + 4y = 94 \end{cases} \)

一元二次方程

\(ax^{2} + bx + c = 0\)，其中 a b c 都是实数，且 \(a \not \equiv 0\)

求根公式

\(x_{1, 2} = \frac{-b\pm\sqrt{b^{2}-4ac}}{2a}\)

判别式（discriminant）

\(\Delta = b^{2} - 4ac\)

注：以上内容均摘自生姜博士的鸢尾花书系列-Book_3《数学要素》