【DP】复健总结 1：入门

前言

DP 一直蒻下去不太好，得逼自己复健一下 DP 了。

感觉自己在 DP 这一块始终没有一个完整的做题思路，选择推倒重建。

DP 与爆搜与记忆化搜索

不考虑最优子结构、状态转移方程这一些之乎者也式的高深词汇，先来讲讲 DP 和爆搜的联系。

比如说在考试时拿到一道题目，我们可以先想到一个暴力的搜索解法，这样的算法的复杂度基本上都是指数级别的，通过对重复统计答案的冗余时间开销剪枝来达成优化时间复杂度的目的。

我们想想这种剪枝优化复杂度的手段的本质是什么，其实是将重复的部分聪明地只计算一次，让爆搜充满记忆，也就是我们所说的记忆化搜索。

比如说：

例题：求斐波那契数列第 \(x\) 项 \(f(x)\) 的值，其中 \(f(0)=0,f(1)=1,f(n)=f(n-1)+f(n-2)\)。

我们不难直接根据题意写出递归代码（搜索的实现方式就是递归嘛）：

int f(int x)
{
	if(x == 0)
	{
		return 0;
	}
	if(x == 1)
	{
		return 1;
	}
	
	return f(x - 1) + f(x - 2);
}

我们看看复杂度是多少，先画出递归树（树中每个节点代表斐波那契数列的项数，以 \(f(6)\) 为例）：

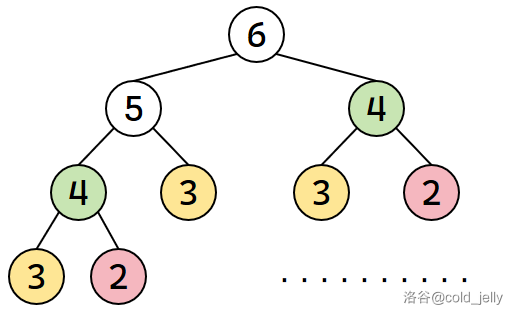
用颜色标记的 \(f(4),f(3),f(2)\) 等被重复访问，如果不做剪枝处理的话，整个递归树（二叉树）的规模可能达到 \(2^n\) 级别，复杂度为 \(O(2^n)\)。

如果我们考虑存储我们已经得到的 \(f\) 值，那么重复访问的信息被剪枝，每个 \(f\) 只会被访问一遍，因此复杂度被直接优化到线性。

const int N = _______;

int F[N];

int f(int x)
{
	if(x == 0)
	{
		return 0;
	}
	if(x == 1)
	{
		return 1;
	}
	if(F[x] != 0)//记忆化
	{
		return F[x];
	}
	
	return F[x] = f(x - 1) + f(x - 2);
}

注意看我们这份记忆化搜索代码中的这一句话：return F[x] = f(x - 1) + f(x - 2);。它实际上就是一个递推公式，反映了我们求 \(f(x)\) 只需知道 \(f(x-1)\) 和 \(f(x-2)\) 的值。那么我们可以将其改写为递推形式：

const int N = _______;

int n;
int f[N];

int main()
{
	f[0] = 0, f[1] = 1;
	for(int i = 2; i < N; i ++)
	{
		f[i] = f[i - 1] + f[i - 2];
	}
	
	return 0;
}

复杂度同样为线性。

注意我们上述的思维过程：我们先得到了暴力的递归 \(O(2^n)\) 做法，然后通过剪枝优化成线性，最后再等价改写为递推形式。虽然求斐波那契数列的问题不能算为传统意义上的 DP，但是这种思维过程与 DP 类似，不妨借过来解释一下 DP。

我们知道，DP 有两种实现方式：递推和记忆化搜索（简称记搜）。上面我们得到的两种线性求斐波那契数列的做法实际上就分别是记搜和递推。这两种做法有什么共同点呢？不难看出，它们的复杂度之所以是线性，而不是指数级，正是因为它们避免了重复计算子问题，也就是 DP 的其中一个要素：重叠子问题。

而我们求得的 \(f\) 值不会被之后的计算过程所改变，这就是 DP 的无后效性。

在递归树中，\(O(2^n)\) 复杂度的做法的遍历方式是自上而下的，在未到达终止条件时，底下的若干状态都是未知的，于是这种做法不可避免地重复遍历了子问题。因此我们在线性递推做法中采用了自下而上的做法，归结起来就是从最基础的初始状态（在本题中就是 \(f(0),f(1)\)）一步一步递推得到我们想求的结果，而这个递推过程的实现即是状态转移，用到的载体是状态转移方程（本题中的 \(f(n)=f(n-1)+f(n-2)\)）。

最优子结构

DP 还有一个要素：最优子结构，最优子结构性质指出，我们在 DP 过程中求得的子问题一定是全局最优解。

例题：数字三角形。

作为 DP 的经典入门题，通过它来解释最优子结构。

我们按照上一题的方式，可以先想到暴力搜索的做法，直接暴力枚举所有路径，复杂度显然是指数级别的。我们固然可以通过记录已求得的子问题的答案来将复杂度优化到 \(O(n^2)\)，但我们不妨直接想想如何自下而上地递推求解呢？我们可以从倒数第一层开始向上扩展，每层之间的扩展即记录当前的最长路径：

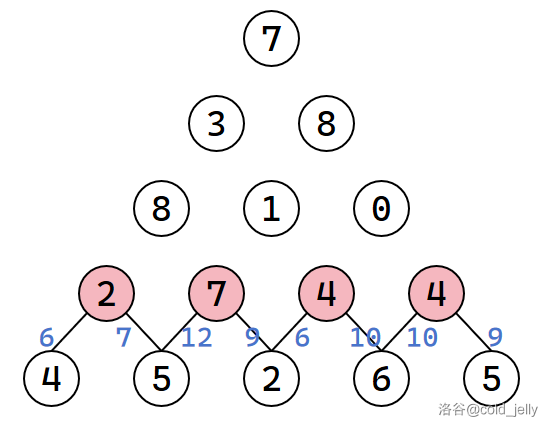
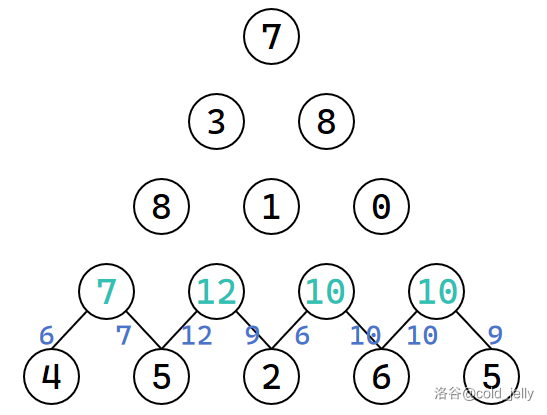
这样一直到最上面的起始点，可求得答案为 \(30\)。

上面“扩展”的过程，实际上就是一个自下而上地递推的 DP 过程，因此我们可以写出：

f[i][j] += max(f[i + 1][j], f[i + 1][j + 1]);

在以上的推导中，我们知道每一层节点到底部的最长路径依赖于它下层的左右节点的最长路径，求得的下层两个节点的最长路径对于依赖于它们的节点来说就是最优子结构，最优子结构对于子问题来说属于全局最优解，这样我们不必去求节点到最底层的所有路径了，只需要依赖于它的最优子结构即可推导出我们所要求的最优解。所以最优子结构有两层含义，一是它是子问题的全局最优解，依赖于它的上层问题只要根据已求得的最优子结构推导求解即可得全局最优解，二是它有缓存的含义，这样就避免了多个依赖于它的问题的重复求解（消除重叠子问题）。