【树状数组】总结

树状数组是一种能够动态维护序列前缀和的数据结构。

树状数组的基本原理

先贴个图：

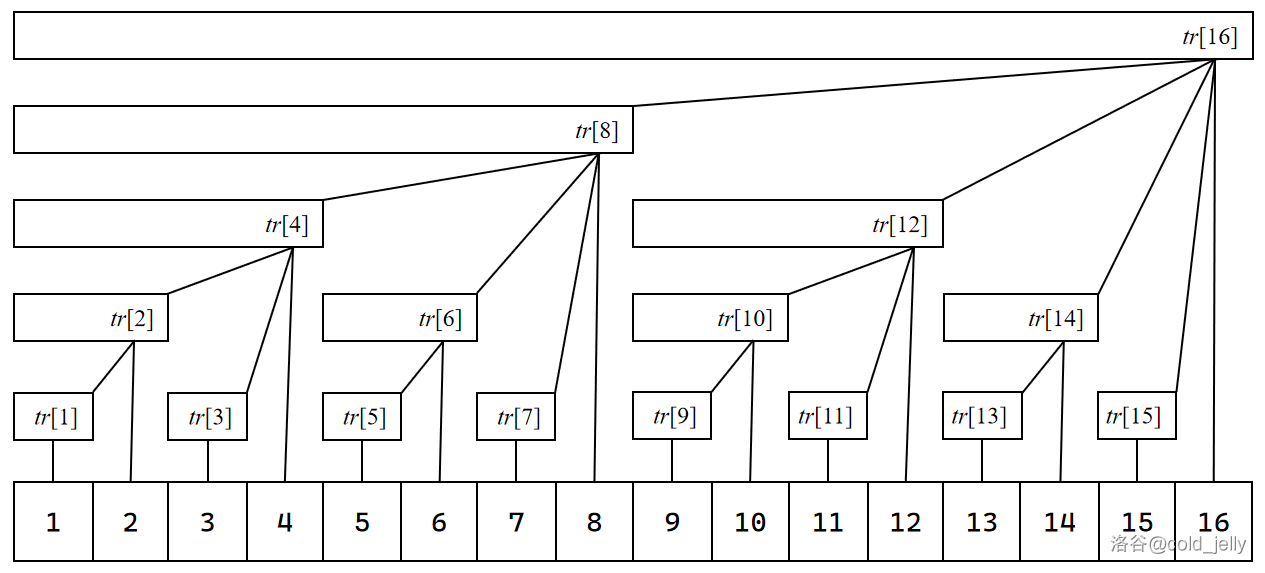
对于一个给定的长度为 \(n\) 的序列 \(a\)，我们建立一个数组 \(tr\)，其中：

\[\boxed{tr[x]=\sum^{x}_{i=x-\text{lowbit}(x)+1}a[i]} \]

\(\text{lowbit}(x)\) 为 lowbit 函数，其值等于 \(x\&(-x)\)。这个数组 \(tr\) 可以看作上图所展示的一个树形结构，例如 \(\text{lowbit}(12)=4\)，则在上图中，\(\displaystyle tr[12]=\sum^{12}_{i=9}a[i]=a[9]+a[10]+a[11]+a[12]\)。

我们发现树状数组的结构满足以下性质：

• 树状数组的叶子节点即为原序列 \(a\) 的对应的数值；
• \(tr[x]\) 保存了以其为根节点的子树中所有的叶子节点的数值之和；
• 除了树状数组的根节点 \(tr[n]\) 外，\(tr[x]\) 的父节点为 \(tr[x+\text{lowbit}(x)]\)；
• 树的深度为 \(\log n\)。

根据整数的二次幂分解的性质，我们可以将序列 \(a\) 的前缀分为不超过 \(\log n\) 个小区间，然后用树状数组快速计算前缀和，时间复杂度为 \(O(\log n)\)，写出代码：

	int query(int x)
	{
		int res = 0;
		for(int i = x; i; i -= lowbit(i))
			res += tr[i];
		return res;
	}

若要求区间 \([l,r]\) 之间的所有数之和，则计算 query(r) - query(l - 1) 即可。

树状数组还支持单点修改，即支持在反复在原序列 \(a\) 的多个位置上分别加减数的过程中维护其前缀和。当我们将 \(a[x]\) 加 \(k\) 时，为维护前缀和，树状数组将会将 \(a[x]\) 到根节点的路径上的所有节点的权值均增加 \(k\)，此时每次将下标加 \(\text{lowbit}(x)\) 即可遍历所有祖先节点了，时间复杂度也为 \(O(\log n)\)。

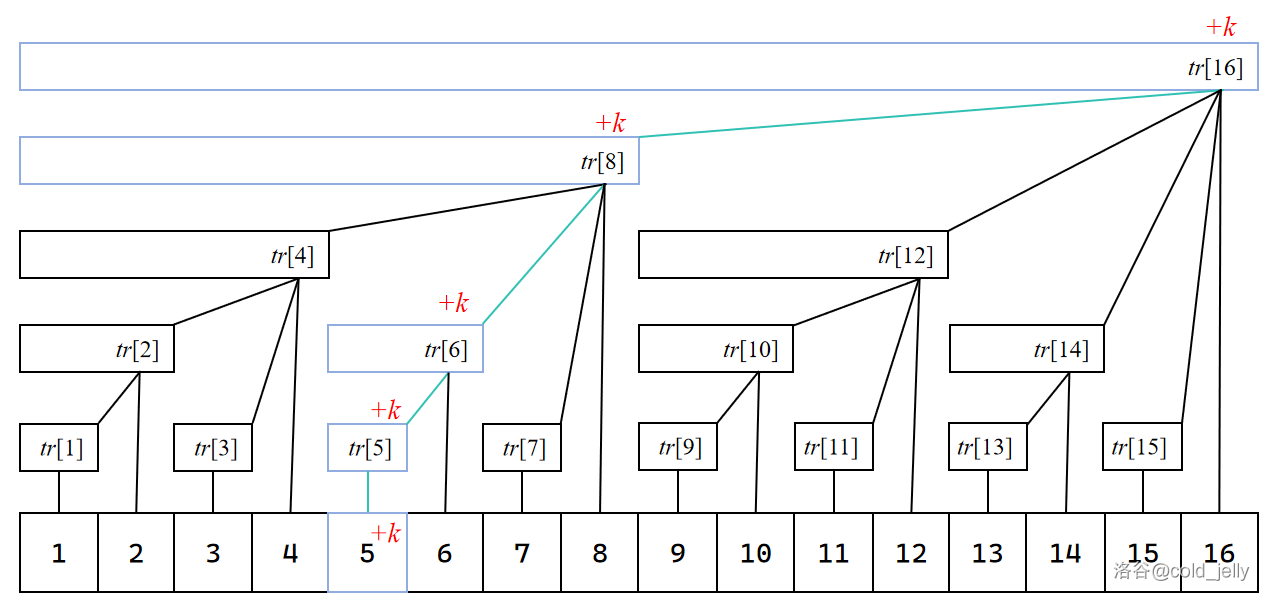
写成代码是：

	void modify(int x, int k)
	{
		for(int i = x; i <= n; i += lowbit(i))
			tr[i] += k;
	}

这里给出结构体封装的树状数组，包含最基础的单点修改（modify）和区间查询（query）操作：

struct FenwickTree
{
	int tr[N];
	inline int lowbit(int x)
	{
		return x & -x;
	}
	void modify(int x, int k)
	{
		for(int i = x; i <= n; i += lowbit(i))
			tr[i] += k;
	}
	int query(int x)
	{
		int res = 0;
		for(int i = x; i; i -= lowbit(i))
			res += tr[i];
		return res;
	}
}T;

树状数组求逆序对

我们知道对于序列 \(\{a_n\}\)，满足 \(a_i>a_j\) 且 \(i<j\) 的数对 \((i,j)\) 被称为逆序对。我们现在使用树状数组求逆序对。

转化一下思维，我们可以先按照 \(a\) 的权值从大到小排序，现在要求的就是对于一个点有多少在他前面的点下标小于这个点。

此时我们可以用树状数组维护。从头到尾扫一遍，对于每个点，逆序对个数就是在这个点下标之前的下标有几个已经被访问过，在将这个点在树状数组 \(tr\) 中加 \(1\)，表示其被访问过，注意判相同元素：

	for(int i = 1; i <= n; i ++)
	{
		ans += T.query(a[i].id);
		T.modify(a[i].id, 1);
	}

总代码：

#include<bits/stdc++.h>
using namespace std;
const int N = 1e5 + 10;
int n, ans = 0;
struct Node
{
	int num, id;
}a[N];
inline bool cmp(Node A, Node B)
{
	if(A.num == B.num) return A.id > B.id;
	return A.num > B.num;
}
struct FenwickTree
{
	int tr[N];
	inline int lowbit(int x)
	{
		return x & -x;
	}
	void modify(int x, int k)
	{
		for(int i = x; i <= n; i += lowbit(i))
			tr[i] += k;
	}
	int query(int x)
	{
		int res = 0;
		for(int i = x; i; i -= lowbit(i))
			res += tr[i];
		return res;
	}
}T;
int main()
{
	cin >> n;
	for(int i = 1; i <= n; i ++)
	{
		scanf("%d", &a[i].num);
		a[i].id = i;
	}
	sort(a + 1, a + 1 + n, cmp);
	for(int i = 1; i <= n; i ++)
	{
		ans += T.query(a[i].id);
		T.modify(a[i].id, 1);
	}
	cout << ans;
	return 0;
}

二维树状数组

一维树状数组可以解决序列的一些相关问题，扩展到二维，那么二维树状数组便可以维护矩阵的一些信息。

在一维树状数组中，\(tr[x]\) 实际维护了右端点为 \(x\)、区间长度为 \(\text{lowbit}(x)\) 的区间的数值和。类似地，在二维树状数组中，我们定义 \(tr[x][y]\) 维护右下角为 \((x,y)\)、长和宽分别为 \(\text{lowbit}(x),\text{lowbit}(y)\) 的矩形内所有数值的和。

这样我们可以写出二维树状数组的单点修改（modify）和区间查询（query）操作了：

struct FenwickTree
{
	int tr[N][N];
	inline int lowbit(int x)
	{
		return x & -x;
	}
	void modify(int x, int y, int k)//(x, y) + k 
	{
		for(int i = x; i <= n; i += lowbit(i))
			for(int j = y; j <= m; j += lowbit(j))
				tr[i][j] += k;
	}
	int query(int x, int y)//求 sum (1, 1) -> (x, y) 
	{
		int res = 0;
		for(int i = x; i; i -= lowbit(i))
			for(int j = y; j; j -= lowbit(j))
				res += tr[i][j];
		return res;
	}
}T;

如果我们要求左上角为 \((a,b)\)、右下角为 \((c,d)\) 的矩形的数值和，我们根据容斥原理，只需要计算 query(c, d) - query(a - 1, d) - query(c, b - 1) + query(a - 1, b - 1) 即可。

树状数组的区间修改，单点查询

乍一看树状数组好像无法支持区间修改操作，但我们可以发挥人类智慧，用一些手段使区间操作变成单点操作。

我会差分！所以我们可以计算原数组的差分数组 \(B[i]=a[i]-a[i-1]\)，那么我们给区间 \([l,r]\) 都加上 \(k\) 时，只需将 \(B[l]\) 加上 \(k\)，\(B[r+1]\) 减去 \(k\) 即可。

单点查询的话，由于差分和前缀和互为逆运算，有 \(\displaystyle a[i]=\sum^{i}_{j=1}B[j]\)。那么我们计算 \(B\) 的前缀和即可。

代码如下：

struct FenwickTree
{
	int tr[N];
	inline int lowbit(int x)
	{
		return x & -x;
	}
	void modify(int x, int k)
	{
		for(int i = x; i <= n; i += lowbit(i))
			tr[i] += k;
	}
	void Rmodify(int l, int r, int k)//区间修改 
	{
		modify(l, k);
		modify(r + 1, -k);
	}
	int query(int x)
	{
		int res = 0;
		for(int i = x; i; i -= lowbit(i))
			res += tr[i];
		return res;
	}
}T;

注意此处 \(tr\) 数组维护的序列是原序列的差分数组 \(B\)。

树状数组的区间修改，区间查询

基于区间修改的思路，树状数组能否继续支持区间查询呢？这里推一下式子。

区间查询的本质就是快速计算前缀和，即 \(\displaystyle \sum^{x}_{i=1}a[i]\)。由于我们的 \(tr\) 数组维护的是差分数组 \(B\)，因此我们做转化：

\[\sum^{x}_{i=1}a[i]=\sum^{x}_{i=1}\sum^{i}_{j=1}B[j] \]

这里我们发现，在累加的过程中，内层 \(B[p]\) 总共在答案中出现了 \(x-p+1\) 次，也就是说：

\[\sum^{x}_{i=1}\sum^{i}_{j=1}B[j]=\sum^{x}_{i=1}(x-i+1)\times B[i]=(x+1)\sum^{x}_{i=1}B[i]-\sum^{x}_{i=1}i\times B[i] \]

那么我们便可以维护 \(B[i]\) 和 \(i\times B[i]\) 的前缀和来快速计算区间和：

struct FenwickTree
{
	int tr1[N], tr2[N];//两个前缀和 
	inline int lowbit(int x)
	{
		return x & -x;
	}
	void modify(int x, int k)
	{
		for(int i = x; i <= n; i += lowbit(i))
			tr1[i] += k, tr2[i] += k * x;
	}
	void Rmodify(int l, int r, int k)//区间修改 
	{
		modify(l, k);
		modify(r + 1, -k);
	}
	int query(int x)
	{
		int res = 0;
		for(int i = x; i; i -= lowbit(i))
			res += (x + 1) * tr1[i] - tr2[i];
		return res;
	}
	int Rquery(int l, int r)//区间查询 
	{
		return query(r) - query(l - 1);
	}
}T;