【图论】总结 13：二分图覆盖和独立集

二分图最小点覆盖

给定二分图 \(G=(V,E)\)，求最小的点集 \(V'\) 使得图中任意一条边都至少有一个端点属于 \(V'\)。这个问题称为二分图的最小点覆盖问题。

对于最小点覆盖问题，我们有：

定理：二分图的最小点覆盖问题等价于求二分图的最大匹配。若二分图的最小点覆盖为 \(V'\)，最大匹配为 \(E'\)，则有关系 \(|V'|=|E'|\)。

证明略。

例题：UVA1194 Machine Schedule。

这是二分图最小点覆盖的模板题。对于每个任务，首先如果 \(a[i]=0\) 或者 \(b[i]=0\)，我们可以在一开始的时候处理，这些不计入答案。

除此之外，每个任务要么在 \(A\) 上使用模式 \(a[i]\) 执行，要么在 \(B\) 上使用模式 \(b[i]\) 执行，二者必选其一。我们尝试将其化归为最小点覆盖问题求解。

我们将 \(A\) 机器的 \(n\) 种模式视为二分图的左部的 \(n\) 个点，将 \(B\) 机器的 \(m\) 种模式视为右部的 \(m\) 个点。我们刻画每个任务可以用连边 \((a[i],b[i])\) 表示每个任务至少需要连边的端点来执行，这样我们求最小点覆盖即可。而由定理，我们用匈牙利算法求出最大匹配即可。

#include<bits/stdc++.h>
using namespace std;
const int N = 1e2 + 10, K = 1e3 + 10;
int n, m, k, ans;
vector<int> e[N * 2];
bool st[N * 2];
int match[N * 2];
void init()
{
	ans = 0;
	for(int i = 1; i <= 200; i ++) e[i].clear();
	memset(match, 0, sizeof match);
}
bool Hungary(int u)
{
	for(auto v : e[u])
	{
		if(!st[v])
		{
			st[v] = true;
			if(!match[v] || Hungary(match[v]))
			{
				match[v] = u;
				return true;
			}
		}
	}
	return false;
}
int main()
{
	while(cin >> n, n)
	{
		cin >> m >> k;
		init();
		for(int i = 1; i <= k; i ++)
		{
			int id, a, b;
			scanf("%d%d%d", &id, &a, &b);
			if(!a || !b) continue;
			e[a].push_back(b + n);
			e[b + n].push_back(a);
		}
		for(int i = 1; i <= n; i ++)
		{
			memset(st, false, sizeof st);
			if(Hungary(i)) ans ++;
		}
		printf("%d\n", ans);
	}
	return 0;
}

二分图最大独立集

对于一张二分图 \(G=(V,E)\)，其中满足任意两点之间都无边相连的点集 \(V'\) 被称为二分图的独立集，其中 \(|V'|\) 最大的被称为二分图的最大独立集。

对于二分图的最大独立集问题，我们有：

定理：二分图的最大独立集问题等价于求二分图的最大匹配。若二分图的最大独立集为 \(V'\)，最大匹配为 \(E'\)，则有关系 \(|V'|=|V|-|E'|\)。

证明略。

例题：P10939 骑士放置。

我们发现在国际象棋棋盘中，骑士所走的日字形的两对角格的颜色一定不同：

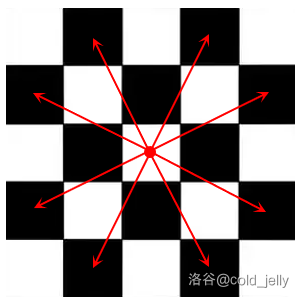
我们可以利用这个性质，把棋盘黑白染色，再把白块和黑块分别作为左部和右部。并且将日字形对角两格连边得到一张二分图，跑匈牙利算法得最大匹配 \(|E'|\)，答案即为 \(nm-T-|E'|\)。

#include<bits/stdc++.h>
using namespace std;
const int N = 1e2 + 10;
int n, m, t, ans = 0;
bool ban[N][N];
int dx[8] = {2, 1, -1, -2, -2, -1, 1, 2};
int dy[8] = {1, 2, 2, 1, -1, -2, -2, -1};
vector<int> e[N * N];
int num(int x, int y)
{
	return (x - 1) * m + y;
}
//set<int> S1, S;
bool st[N * N];
int match[N * N];
bool Hungary(int u)
{
	for(auto v : e[u])
	{
		if(!st[v])
		{
			st[v] = true;
			if(!match[v] || Hungary(match[v]))
			{
				match[v] = u;
				return true;
			}
		}
	}
	return false;
}
int main()
{
	cin >> n >> m >> t;
	for(int i = 1; i <= t; i ++)
	{
		int x, y;
		scanf("%d%d", &x, &y);
		ban[x][y] = true;
	}
	for(int i = 1; i <= n; i ++)
	{
		for(int j = 1; j <= m; j ++)
		{
			if(!ban[i][j])
			{
				for(int I = 0; I < 8; I ++)
				{
					int nx = i + dx[I];
					int ny = j + dy[I];
					if(nx < 1 || nx > n || ny < 1 || ny > m || ban[nx][ny]) continue;
					if(nx + ny & 1)
					{
						int u = num(i, j), v = num(nx, ny);
						e[u].push_back(v);
						e[v].push_back(u);	
					}
				}
			}
		}
	}
	for(int i = 1; i <= n * m; i ++)
	{
		memset(st, false, sizeof st);
		if(Hungary(i)) ans ++;
	}
	ans /= 2;//跑了两遍，除以 2
	cout << n * m - t - ans;
	return 0;
}