【图论】总结 12：二分图匹配

二分图

如果一张无向图 \(G=(V,E)\) 存在点集 \(A,B\)，满足 \(|A|,|B|\ne \varnothing\) 且 \(A\cap B=\varnothing,A\cup B=V\)，且不存在这样的边 \((u,v)\) 满足 \(u,v\in A(\text{or }u,v\in B)\)，那么该无向图称为一张二分图。\(A\) 和 \(B\) 被称为二分图的左部和右部。

说人话就是如果能把一张图的所有点划分为两个非空点集，且同一集合之间的点无边相连，那么这样的无向图被称作二分图。

例如下面的图就是一张二分图：

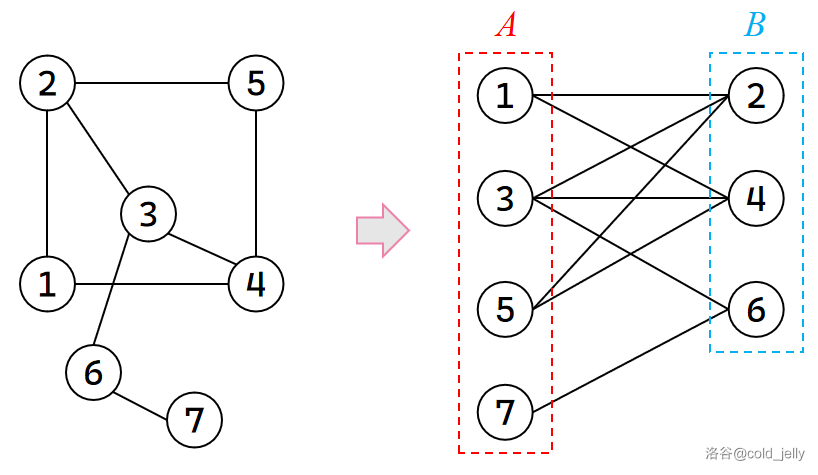
二分图的判定

定理：一张图是二分图 \(\Leftrightarrow\) 图上不存在奇环 \(\Leftrightarrow\) 给图二染色的过程中不存在矛盾。

为判定奇环，我们采用染色法。算法流程如下：

1. 所有节点初始无颜色；
2. 从一个无颜色的节点 \(S\) 开始，将它染色为 \(col\)（\(col\in\{1,2\}\)，表示白色或黑色）；
3. 从 \(S\) 出发跑 DFS，对于当前节点 \(u\)，遍历它的相邻节点 \(v\)；
4. 如果 \(v\) 无颜色，则将 \(v\) 染成与 \(u\) 不同的颜色；如果 \(v\) 与 \(u\) 颜色不同，继续遍历即可；如果 \(v\) 与 \(u\) 的颜色相同，则证明该图不是二分图。

时间复杂度为 \(O(n+m)\)。

const int N = _______, M = _______;
int color[N];//默认无颜色时为 0 
bool dfs(int u, int col)
{
	color[u] = col;
	for(auto v : e[u])
	{
		if(color[v] == color[u]) return false;
		if(!color[v] && !dfs(v, 3 - color[u])) return false;
	}
	return true;
}

二分图最大匹配

对于图 \(G=(V,E)\)，如果边集 \(E'\) 是 \(E\) 的子集，且满足该边集中任意两条边都没有公共端点，那么我们称 \(E'\) 为图 \(G\) 的一组匹配。对于二分图，使得 \(|E'|\) 最大的一组匹配称为二分图的最大匹配。

对于一组匹配 \(E'\)，我们称属于 \(E'\) 的边为匹配边，不属于 \(E'\) 的边为非匹配边。所有匹配边的端点称为匹配点，其余的点称为非匹配点。

在二分图中，如果存在一条路径 \(path\) 连接两个非匹配点，并使得非匹配边与匹配边在 \(path\) 上交替出现，那么称 \(path\) 为匹配 \(E'\) 的一条增广路。

增广路有如下性质：

• 增广路的长度 \(L\) 为奇数（这里的长度指边数）；
• 给路径上的所有边编号 \(1\sim L\)，其中奇数序号的为非匹配边，偶数序号的为匹配边。

定理：二分图的一组匹配 \(E'\) 是最大匹配，当且仅当图中不存在 \(E'\) 的增广路。

证明考虑反证法。假设 \(E'\) 是最大匹配且存在增广路 \(path\)，记 \(path\) 的长度为 \(L\)，那么编号为偶数的边 \(2,4,6,\dots,L-1\) 组成 \(E'\)。此时显然有边集 \(E''=\{1,3,5,\dots,L\}\) 也是原图的一个匹配，发现 \(|E''|=|E'|+1\)，与 \(E'\) 是最大匹配矛盾，故得证。

如何求一张二分图的最大匹配呢？我们采用匈牙利算法。

匈牙利算法的大致流程如下（我们记 \(E'\) 为现阶段求得的最大匹配）：

1. 初始时所有边都不是匹配边，\(E'=\varnothing\)；
2. 枚举二分图左部上的点 \(u\in A\)，并给 \(u\) 寻找与其有连边的右部点 \(v\in B\)，当 \(v\) 为非匹配点或者 \(v\) 已与另一个 \(u'\in A\) 匹配，但 \(u'\) 还能找到其它的 \(v'\in B\) 与其匹配时，我们称其匹配成功（即找到了增广路）；
3. 重复第二步，直到找不到增广路。

我们用一个例子来解释匈牙利算法的流程。假设对于下面这张二分图，我们要求它的最大匹配：

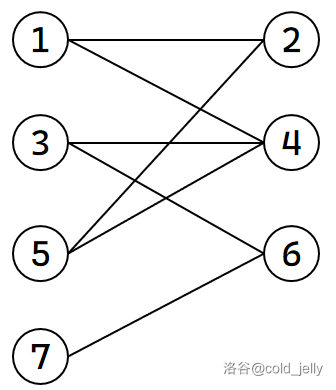
我们遍历左部节点，首先给 \(1\) 匹配 \(2\) 号节点：

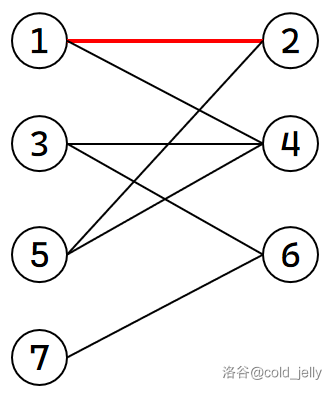
然后给 \(3\) 匹配 \(4\) 号节点：

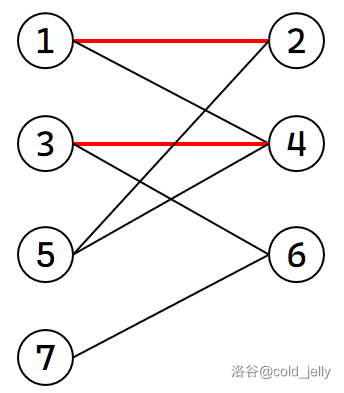
我们现在要给 \(5\) 号匹配了，但是与 \(5\) 号节点相连的 \(2\) 号和 \(4\) 号都已匹配，我们就考虑尝试给 \(1\) 号节点找其它的匹配对象（下图中黄色边表示临时拆开匹配）：

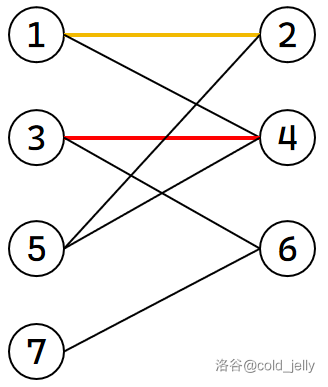
但是与 \(1\) 号节点相连的剩下的节点 \(4\) 也已与 \(3\) 匹配，那么我们尝试给 \(3\) 再找新的匹配对象：

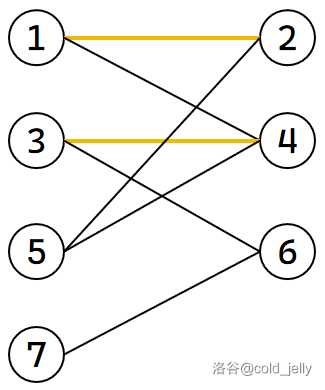
我们发现 \(3\) 还可以与 \(6\) 匹配，我们把它们匹配上：

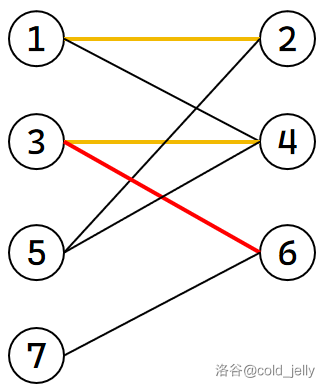
然后我们回溯再将 \(1\) 与 \(4\) 匹配，\(5\) 与 \(2\) 匹配：

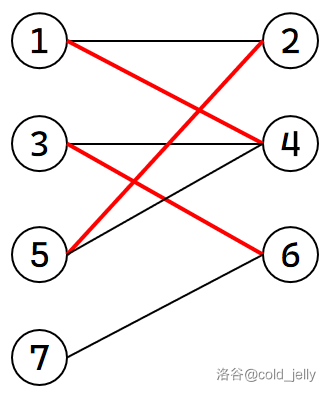
接下来我们遍历到 \(7\)，很遗憾我们并不能再腾出一个位置给它匹配了。我们最终求得的最大匹配即为：

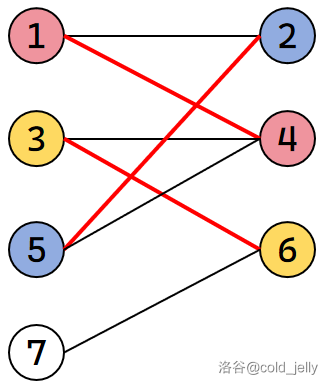
我们写出匈牙利算法的模板：

bool st[N];//记录节点 i 在试图改变匹配时成功与否 
int match[N];//记录左部节点 i 的匹配对象 
bool Hungary(int u)//匈牙利算法 
{
	for(auto v : e[u])
	{
		if(!st[v])
		{
			st[v] = true;
			if(!match[v] || Hungary(match(v)))
			{
				match[u] = v;
				return true;
			}
		}
	}
	return false;
}
int main()
{
	int ans = 0;//最大匹配数 
	for(int i = 1; i <= n; i ++)
	{
		memset(st, false, sizeof st);
		if(Hungary(i)) ans ++;
	}
}

例题：P3386 【模板】二分图最大匹配。

代码如下：

#include<bits/stdc++.h>
using namespace std;
const int N = 1e3 + 10, M = 1e5 + 10;
int n, m, E, ans = 0;
vector<int> e[N];
bool st[N];
int match[N];
bool Hungary(int u)
{
	for(auto v : e[u])
	{
		if(!st[v])
		{
			st[v] = true;
			if(!match[v] || Hungary(match[v]))
			{
				match[v] = u;
				return true;
			}
		}
	}
	return false;
}
int main()
{
	cin >> n >> m >> E;
	for(int i = 1; i <= E; i ++)
	{
		int u, v;
		scanf("%d%d", &u, &v);
		e[u].push_back(v + n);
	}
	for(int i = 1; i <= n; i ++)
	{
		memset(st, false, sizeof st);
		if(Hungary(i)) ans ++;
	}
	cout << ans;
	return 0;
}

二分图完美匹配

对于一张含有偶数个点的二分图（假定节点数为 \(n\)），若其左部与右部的节点数均为 \(\dfrac{n}{2}\)，且该二分图的最大匹配数为 \(\dfrac{n}{2}\)，那么我们称这个二分图具有完美匹配。

完美匹配的判定是好做的，而求二分图的完美匹配的方法与求最大匹配相同。

多重匹配问题

在一张二分图 \(G=(V,E)\) 中，设左部为 \(A\)、右部为 \(B\)，现在我们要从中选尽可能多的边，满足第 \(i\) 个左部节点至多选 \(el_i\) 条出边与右部节点相连、第 \(j\) 个右部节点至多选 \(er_i\) 条出边与左部节点相连。我们把这种问题称作二分图的多重匹配问题。

不难发现，当 \(\forall i,j,\text{st. }el_i=er_j=1\) 时，问题转变成了二分图最大匹配问题。

根据这种问题之间的联系，我们可以用拆点的方法求解多重匹配问题。具体而言，我们把第 \(i\) 个节点 \(u\) 拆分成 \(el_i\) 个不同的左部节点，把第 \(j\) 个节点 \(v\) 拆分成 \(er_j\) 个不同的右部节点。然后对于原图中的边 \((u,v)\)，我们将拆点后的每个左部节点与右部节点连边。这样我们就将多重匹配问题转化为了一般的最大匹配问题。

例题：P10936 导弹防御塔。

我们发现我们可以二分时间，判定当前时间 \(mid\) 内能否击退所有入侵者。

此外，由于一个防御塔可对应多个入侵者，所以这是一个多重匹配问题，我们考虑将一个防御塔拆成若干点。发现在已知 \(mid\) 和 \(T_1,T_2\) 后，我们可求得在 \(mid\) 分钟内防御塔可发射的导弹数量 \(p=\dfrac{mid+T_2}{T_1+T_2}\)。然后我们就可以将一个防御塔拆成 \(p\) 个点，连边后跑匈牙利算法即可。

#include<bits/stdc++.h>
using namespace std;
const int N = 1e4 + 10, M = 1e6 + 10;
const double eps = 1e-7;
int n, m;
double T1, T2, V;
double l = 0, r = 1e9;
struct Point
{
	double x, y;
}defend[N], attack[N];//防御塔和入侵者 
bool st[N];
int match[N];
int h[N], e[M], ne[M], ide;
inline void add(int u, int v)
{
	e[ide] = v, ne[ide] = h[u], h[u] = ide ++;
}
bool Hungary(int u)
{
	for(int i = h[u]; ~i; i = ne[i])
	{
		int v = e[i];
		if(!st[v])
		{
			st[v] = true;
			if(!match[v] || Hungary(match[v]))
			{
				match[v] = u;
				return true;
			}	
		}
	}
	return false;
}
//第 i 个入侵者和第 j 个防御塔的距离 
inline double dist(int i, int j)
{
	double deltax = attack[i].x - defend[j].x;
	double deltay = attack[i].y - defend[j].y;
	return sqrt(deltax * deltax + deltay * deltay);
}
void build(double x)//建边 
{
	int p = max(0, (int)floor((x + T2) / (T1 + T2)));
	p = min(m, p);
	for(int i = 1; i <= m; i ++)
	{
		for(int j = 1; j <= n; j ++)
		{
			for(int k = 1; k <= p; k ++)//拆点 
			{
				double T = dist(i, j) / V;
				T += (k - 1) * 1.0 * (T1 + T2) + T1;
				if(T > x) continue;
				int u = i, v = m + (j - 1) * p + k;
				add(u, v), add(v, u);
			}
		}
	}
}
bool check(double x)
{
	memset(match, 0, sizeof match);
	memset(h, -1, sizeof h);
	ide = 0;
	build(x);
	for(int i = 1; i <= m; i ++)
	{
		memset(st, false, sizeof st);
		if(!Hungary(i)) return false;
	}
	return true;
}
int main()
{
	cin >> n >> m >> T1 >> T2 >> V;
	T1 /= 60;//转为分钟 
	for(int i = 1; i <= m; i ++)
		scanf("%lf%lf", &attack[i].x, &attack[i].y);
	for(int i = 1; i <= n; i ++)
		scanf("%lf%lf", &defend[i].x, &defend[i].y);
	while(r - l > eps)
	{
		double mid = (l + r) / 2;
		if(check(mid)) r = mid;
		else l = mid;
	}
	printf("%.6lf", l);
	return 0;
}