【图论】总结 7：2-SAT

2-SAT 问题的基本模型与建图方法

考虑这样一个问题：给定 \(n\) 个 bool 变量，以及 \(m\) 个条件，每个条件表述为两个变量之间的一条限制关系，求满足所有限制条件的 \(n\) 个 bool 变量的一组合法解。

这个问题被称为 2-SAT 问题。其最原始的最板的问题是：

给定 \(n\) 个 bool 变量 \(\{p_n\}\) 以及 \(m\) 个限制条件，每个限制条件表述为 i a j b，表示若 \(p_i=a\)，则 \(p_j\) 必定为 \(b\)（其中 \(a,b\in \{0,1\}\)）。要求一组合法解。

我们举一个样例（\(n=3,m=5\)）：

1 0 2 0
2 0 1 1
2 1 1 0
1 0 3 1
1 1 3 0

我们假设如果 \(p_1=0\)，那么根据 1 0 2 0 推得 \(p_2=0\)，又根据 2 0 1 1 推得 \(p_1=1\)，发现矛盾了，因此 \(p_1\) 不可能为 \(0\)。以此类推手模样例可以发现该样例只有 \(p_1=1,p_2=0,p_3=0\) 这一组合法解。在这个过程中，我们发现每个条件的“推出”关系可以看作一条由一个变量的取值“这个点”指向另一个变量的取值“这个点”的一条有向边。也就是说对于 2-SAT 问题，我们可以用建图的思想求解。

因此我们不妨为每个变量的 \(0/1\) 取值均建立一个代表性节点。例如样例中的 \(p_1=0/1\) 可对应节点 \(1_0\) 与 \(1_1\)，类似地建立节点 \(2_0,2_1,3_0,3_1\)。为方便表述，我们不妨将 \(1_0,2_0,3_0\) 节点分别编号 \(1\sim 3\)，然后将 \(1_1,2_1,3_1\) 节点分别编号 \(4\sim 6\)。

将上述过程一般化，我们可以总结出 2-SAT 问题的建点方法：将“变量 \(p_i\) 取值 \(0\)”对应为节点 \(i\)，将“变量 \(p_i\) 取值 \(1\)”对应节点 \(i+n\)。这样我们可以得到共 \(2n\) 个节点。

再加上我们上面的建有向边的规则，我们可以建出样例的图：

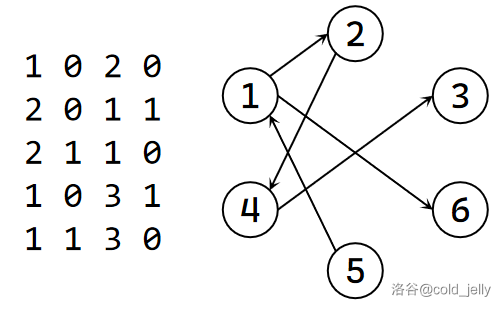
例如有向边 \((1,6)\) 的含义就是“若 \(p_1=0\)，则 \(p_3\) 必定为 \(1\)”。

回归问题，为什么 \(\{1,0,0\}\) 是唯一合法解呢？我们不妨在图上找答案。如果从点 \(1\) 出发，存在这样一条路径：\(1\to 2\to 4\)，这意味着我们由 \(p_1=0\) 推出了 \(p_1=1\)！很显然矛盾，因此 \(p_1\) 不能为 \(0\)；但如果我们从 \(4\) 出发是走不到 \(1\) 的，因此综合得 \(p_1\) 只能为 \(1\)。从 \(5\) 出发存在 \(5\to 1\to 2\)，依然推出矛盾，所以 \(p_2\) 不能为 \(1\)，只能为 \(0\)。而因为 \(p_1=1\)，且有有向边 \((4,3)\)，因此 \(p_3\) 只能为 \(0\)。我们便得出了 \(\{1,0,0\}\) 这一组唯一合法解啦。

我们写出建图的代码（当然这一大坨判断可以用高级的位运算简化）：

	for(int k = 1; k <= m; k ++)
	{
		int i, a, j, b;
		scanf("%d%d%d%d", &i, &a, &j, &b);
		if(a == 0)
		{
			if(b == 0) e[i].push_back(j);
			else e[i].push_back(j + n);
		}
		else
		{
			if(b == 0) e[i + n].push_back(j);
			else e[i + n].push_back(j + n);
		}
	}

在建图之后，我们考虑什么情况下是无解的。根据上述规律，我们发现，如果对于 \(p_i\)，其两种取值对应的节点 \(i\) 和 \(i+n\) 同属于同一个强连通分量时，2-SAT 问题无解，因为此时会出现类似 \(p_1\) 既要是 \(1\) 又要是 \(0\) 这样的矛盾局面。

对于有关强连通分量的问题，我们很自然地想到用 Tarjan 算法求解。求出每个强连通分量后，循环一次，判断每个 \(i\) 和 \(i+n\) 属于的 SCC 颜色（编号）是否相同即可，复杂度为 \(O(n+m)\)。

注意到跑完 Tarjan 后缩点所形成的 DAG 中，每个 SCC 对应的“大点”的拓扑序和它的颜色（编号）大小是对应的（即拓扑序更大的表现为在 Tarjan 时更晚被遍历到，因此更先被弹出栈，其编号更小），而由拓扑序的性质可以知道，拓扑序小的 SCC 到拓扑序大的 SCC 的过程是单向的，也就是拓扑序大的 SCC 不可能有一条出边到拓扑序小的 SCC。因此编号较大的 SCC 单向到达编号较小的 SCC。

而这意味着如果编号较大的那个 SCC 和编号较小的 SCC 里分别含有 \(p_i\) 的两种取值 \(0/1\) 所对应的两个节点 \(u\) 和 \(v\) 的话，那么 \(u\) 是可以单向到达 \(v\) 的，也就对应“\(p_i=0\) 时 \(p_i\) 必须为 \(1\)”，这是矛盾的，因此 \(u\) 是不可以作为合法解中的 \(p_i\) 的取值的。而反过来 \(v\) 是不能到达 \(u\) 的，因此 \(v\) 即为合法解中的 \(p_i\) 的取值。

记 \(u\) 所在的 SCC 的编号为 \(id\) 时符号为 \(id=\text{SCC}(u)\)，综上我们可以总结：

\(p_i\) 两种取值对应的节点为 \(u\) 和 \(v\)。若 \(\text{SCC}(u)>\text{SCC}(v)\)，那么 \(v\) 合法；若 \(\text{SCC}(u)<\text{SCC}(v)\)，那么 \(u\) 合法；若 \(\text{SCC}(u)=\text{SCC}(v)\)，那么该 2-SAT 问题无解。

其实还有一种情况我们没有考虑到，就是如果 \(u\) 和 \(v\) 不可达呢？例如我们回看例子：

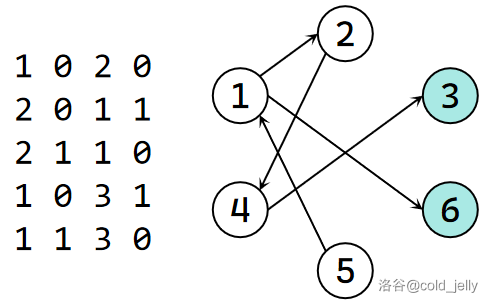
\(p_3\) 对应的节点 \(3\) 和 \(6\) 并没有有向边将它们相连，扩展到缩点后的 DAG 上就是它们所在的 SCC 编号不同且不可达，那么此时我们认为这两种取值无法在已有的条件下推出矛盾，只能通过其它限制推出取值，它们都是有可能成为合法点的。此时为保证解合法，我们选择缩点后 SCC 编号更小的那个作为合法点。

至此，我们根据 SCC 编号大小来得到了 2-SAT 所有可能情况下的合法解。也就是说我们求解 2-SAT 问题只需要跑一遍 Tarjan 算法即可，时间复杂度为 \(O(n+m)\)。

#include<bits/stdc++.h>
using namespace std;
const int N = 2 * (1e5 + 10), M = 5e5 + 10;
int n, m;
vector<int> e[N], e2[N];
int dfn[N], low[N], idx;
stack<int> s;
bool st[N];
int SCC, color[N];
void tarjan(int u)//Tarjan 模板 
{
	dfn[u] = low[u] = ++ idx;
	s.push(u);
	st[u] = true;
	for(auto v : e[u])
	{
		if(!dfn[v])
		{
			tarjan(v);
			low[u] = min(low[u], low[v]);
		}
		else if(st[v]) low[u] = min(low[u], dfn[v]);
	}
	if(low[u] == dfn[u])
	{
		int top;
		SCC ++;
		do
		{
			top = s.top();
			s.pop();
			st[top] = false;
			color[top] = SCC;
		}while(top != u);
	}
}
int main()
{
	cin >> n >> m;
	for(int k = 1; k <= m; k ++)
	{
		int i, a, j, b;
		scanf("%d%d%d%d", &i, &a, &j, &b);
		if(a == 0)
		{
			if(b == 0) e[i].push_back(j);
			else e[i].push_back(j + n);
		}
		else
		{
			if(b == 0) e[i + n].push_back(j);
			else e[i + n].push_back(j + n);
		}
	}
	for(int i = 1; i <= 2 * n; i ++)
		if(!dfn[i]) tarjan(i);
	for(int i = 1; i <= n; i ++)
		if(color[i] == color[i + n]) return puts("-1"), 0;//无解 
	for(int i = 1; i <= n; i ++)
	{
		if(color[i] < color[i + n]) printf("0 ");
		else printf("1 ");
	}
	return 0;
}

2-SAT 问题例题分析

所有的 2-SAT 问题在建图后的方法都一致，因此对于一道 2-SAT 的题目，我们一般只关心其是如何建图的。

我们应将所有的变量之间的肯定的推导关系转化为有向边。这里的“肯定的推导关系”除上面的“若 \(u\) 成立，则 \(v\) 一定成立”（\(u,v\le n\)）这样的 \(u\to v\) 的有向边，还包括另一种情况：“若 \(v\) 不成立，则 \(u\) 一定不成立”，此时我们需要连一条 \(v+n\to u+n\) 的有向边，它对应着“若 \(v+n\) 成立，则 \(u+n\) 一定成立”，这与“若 \(v\) 不成立，则 \(u\) 一定不成立”是等价的。

在补充了建图方式后，来看例题：

例题 \(1\)：P4782 【模板】2-SAT。

我们注意每个条件中至少有一条满足，也就是“一个变量不符要求时，另一个变量必须符合要求”，也就是“一个变量符合相反要求时，另一个变量必须符合要求”，那么对于每个条件建两条边即可：

	for(int k = 1; k <= m; k ++)
	{
		int i, a, j, b;
		scanf("%d%d%d%d", &i, &a, &j, &b);
		if(a == 0)
		{
			if(b == 0) e[i].push_back(j + n), e[j].push_back(i + n);
			else e[i].push_back(j), e[j + n].push_back(i + n);
		}
		else
		{
			if(b == 0) e[j].push_back(i), e[i + n].push_back(j + n);
			else e[i + n].push_back(j), e[j + n].push_back(i);
		}
	}

例题 \(2\)：P5782 [POI 2001] 和平委员会。

同党两人即为同一个变量的 \(0/1\) 取值。如果两人 \(i,j\) 相互厌恶，那么如果选 \(i\)，就必须选 \(j\) 的同党；如果选了 \(j\)，就必须选 \(i\) 的同党。这是上文提到的“肯定的推导关系”，因此我们对于每一个限制建两条边：

	for(int i = 1; i <= m; i ++)
	{
		int u, v;
		scanf("%d%d", &u, &v);
		e[u].push_back(P(v));
		e[v].push_back(P(u));
	}

其中：

int P(int x)//同党
{
	if(x & 1) return x + 1;
	else return x - 1;
}