【图论】总结 4：最小生成树

对于有权无向图 \(G=(V,E)\)，称由 \(G\) 中全部 \(n\) 个顶点以及 \(n-1\) 条边构成的连通图 \(G'\subset G\) 为图 \(G\) 的一棵生成树，而图 \(G\) 的所有生成树里边权和最小的被称为图 \(G\) 的最小生成树（MST）。

Kruskal 算法

Kruskal 算法基于贪心思想，总是维护无向图的最小生成森林。其流程如下：

1. 初始时，生成森林包含 \(0\) 条边，图上每个节点单独作为一棵树；
2. 我们建立并查集，初始时每个点自身构成一个集合；
3. 把图中所有边按照边权从小到大排序，然后按顺序扫描边 \((u,v,w)\)；
4. 如果 \(u,v\) 在同一集合中，直接跳过，否则合并 \(u,v\) 所在的两个集合，同时将 \(w\) 累加进答案；
5. 扫描完毕后，上步中累加的 \(\displaystyle \sum w\) 就是最小生成树的大小。

我们用一个例子来过一遍 Kruskal 算法的流程：

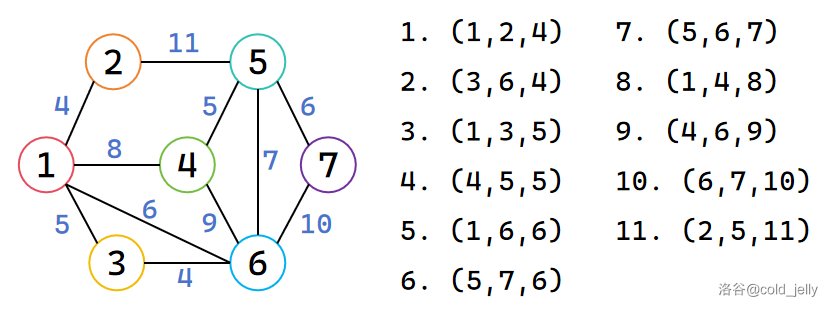
图中相同颜色的点表示属于同一集合。此时我们将所有边按边权从小到大排序，依次扫描。

对于边 \((1,2,4)\)，\(1,2\) 不属于同一集合，因此合并，并累加 MST，边 \((3,6,4)\) 同理：

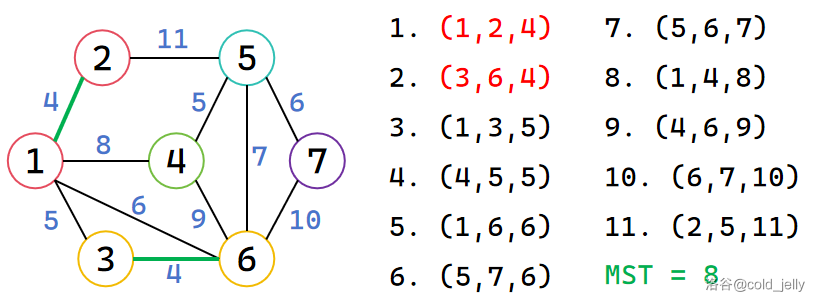
接下来扫描到边 \((1,3,5)\)，\(1,3\) 不属于同一集合，因此合并，并累加 MST，边 \((4,5,5)\) 同理：

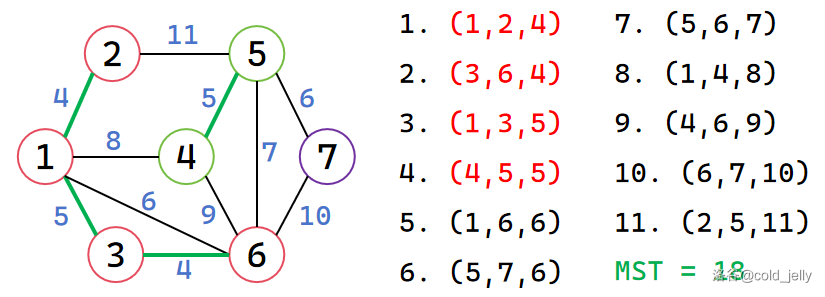
再接下来扫描边 \((1,6,6)\)，\(1,6\) 已属于同一集合，故不做操作；而边 \((5,7,6)\) 中 \(5,7\) 不属于同一集合，因此合并，并累加 MST：

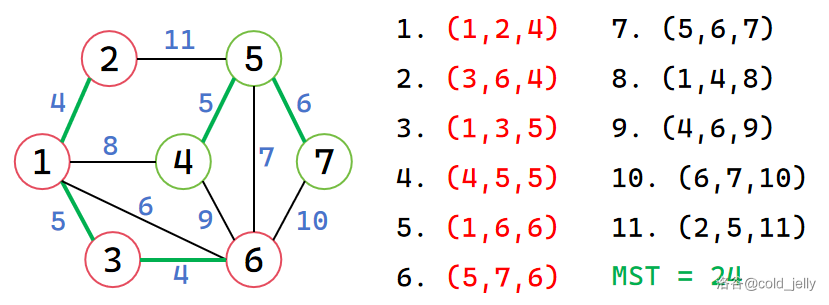
然后扫描边 \((5,6,7)\)，\(5,6\) 不属于同一集合，因此合并，并累加 MST：

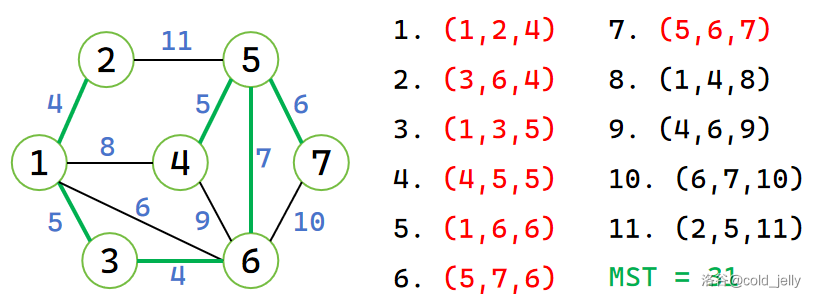
此时我们发现所有点都已属于一个集合，接下来的操作将不会改变 MST，这里将这些步骤略去。最终绿色边及所有点构成的就是 MST 了。

Kruskal 算法的时间复杂度为 \(O(m\log m)\)。我们可以写出代码如下：

#include<bits/stdc++.h>
using namespace std;
const int N = 1e5 + 10, M = 5e5 + 10;
int n, m, MST = 0;
struct Edge
{
	int u, v, w;
}e[M];
inline bool cmp(Edge A, Edge B)
{
	return A.w < B.w;
}
int fa[N];//并查集 
int find(int x)
{
	if(fa[x] == x) return x;
	return fa[x] = find(fa[x]);
}
int main()
{
	cin >> n >> m;
	for(int i = 1; i <= m; i ++)
		scanf("%d%d%d", &e[i].u, &e[i].v, &e[i].w);
	sort(e + 1, e + 1 + m, cmp);
	for(int i = 1; i <= n; i ++) fa[i] = i;
	for(int i = 1; i <= m; i ++)
	{
		int x = find(e[i].u), y = find(e[i].v);
		if(x == y) continue;
		fa[x] = y, MST += e[i].w;
	}
	cout << MST;
	return 0;
}

Prim 算法

Prim 算法是另一种求最小生成树的算法，与 Kruskal 算法不同，其总是维护最小生成树的一部分。流程如下：

1. 初始时 MST 仅包含节点 \(1\)，令已经属于 MST 的节点集合为 \(T\)，其余为 \(S\)；
2. 找到一条边 \((u,v,w)\)，其满足 \(\displaystyle \min_{u\in S,v\in T}\{w\}\)，也就是两端点分属于集合 \(S,T\) 的边权最小的边，令 \(S\setminus \{u\}\to S,T\setminus \{v\}\to T\)，并将 \(w\) 累计入 MST。

为此我们维护数组 \(d\)。若 \(u\in S\)，则 \(d[u]\) 等于 \(u\) 与 \(T\) 中节点的所有连边中最小的边权；若 \(u\in T\)，则 \(d[u]\) 等于 \(u\) 被加入 \(T\) 时选出的最小边的权值。我们给已加入 \(T\) 的节点打上标记，每次从未被标记的节点中选出 \(d\) 值最小的，把它加入 \(T\) 并标记，同时用其出边更新 \(d\) 值。最终 MST 的权值就是 \(\displaystyle \sum^{n}_{i=2}d[i]\)。

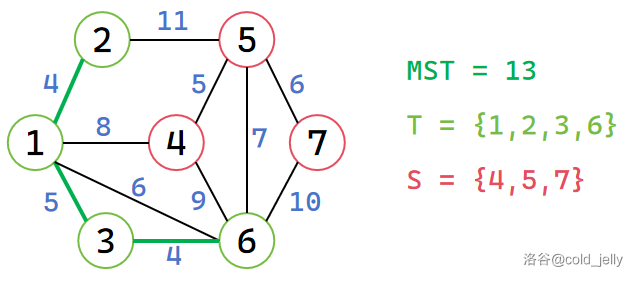
我们仍然用上面的例子过一遍 Prim 算法的流程。初始时仅有 \(1\) 号节点属于 \(T\)（我们用绿色表示属于 \(T\)，红色表示属于 \(S\)），注意，我们在这里为表述方便，将最后 \(d\) 数组的累加表述为在过程中累加：

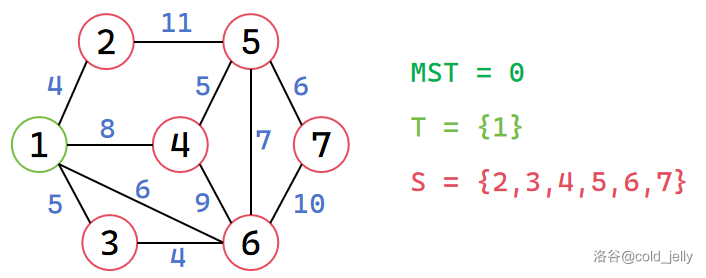
此时未被标记的节点中 \(d\) 值最小的是 \(d[2]=4\)，因此将 \(2\) 加入 \(T\)，同时扫描 \(2\) 的所有出边，更新 \(d[5]=11\)，MST 累加 \(4\)：

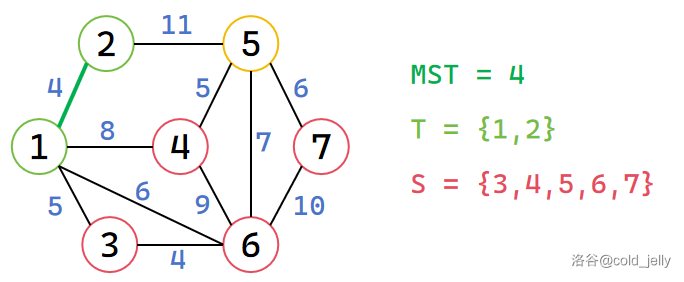
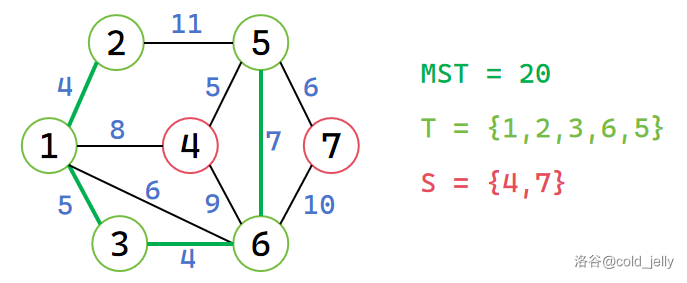
此时未被标记的节点中 \(d\) 值最小的是 \(d[3]=5\)，因此将 \(3\) 加入 \(T\)，同时扫描 \(3\) 的所有出边，更新 \(d[6]=4\)，MST 累加 \(5\)：

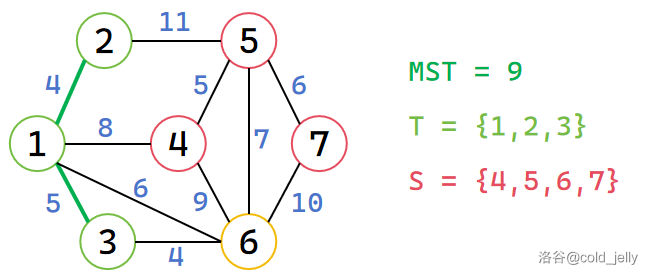
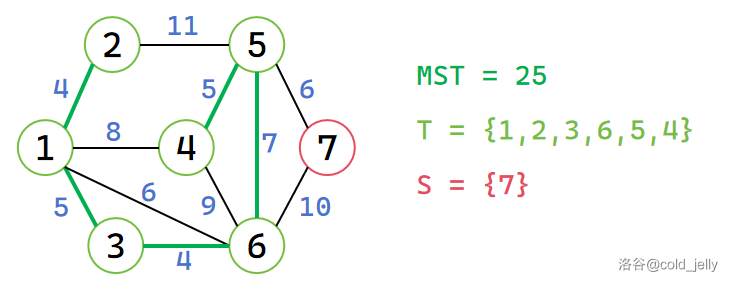
以此类推，我们依次将 \(6,5,4,7\) 号节点加入 \(T\)，最终求得 MST：

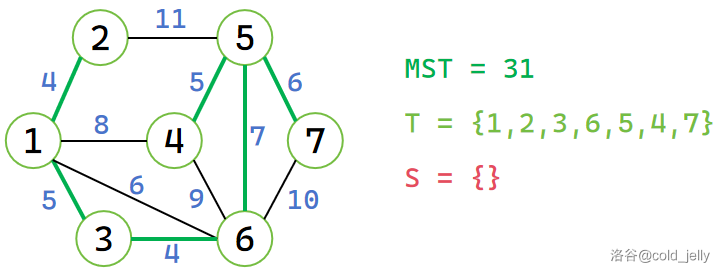
Prim 算法的时间复杂度为 \(O(n^2)\)，可用堆优化至 \(O(m\log n)\)，但实际中不常用。Prim 算法主要用于稠密图的最小生成树的求解。

Prim 算法求 MST 的核心代码如下：

void Prim()
{
	memset(d, 0x3f, sizeof d);
	memset(st, false, sizeof st);
	d[1] = 0;
	for(int i = 1; i < n; i ++)
	{
		int u = 0;
		for(int j = 1; j <= n; j ++)
			if(!st[j] && (u == 0 || d[j] < d[u])) u = j;
		st[u] = true;
		for(int v = 1; v <= n; v ++)
			if(!st[v]) d[v] = min(d[v], w[u][v]);
	}
}