【图论】总结 3：分层图

分层图，顾名思义，就是分成若干层的图，也就是一个立体结构，这一类题的难点在于如何根据题目信息建出合适的图。我们以例题分析。

---

例题 \(1\)：P4568 [JLOI2011] 飞行路线：在普通单源最短路问题的基础上添加了 \(k\) 次“\(0\) 元券”机会。

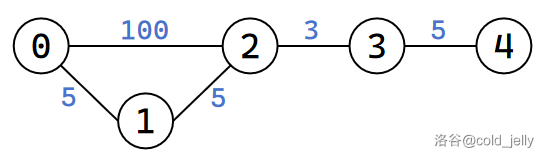
首先对于样例先建出一层图：

考虑如何刻画 \(1\) 次“\(0\) 元券”机会，我们可以把这一次机会想象成一个“阶段”，每一次我们在某个节点时都可以选择用掉 \(1\) 次机会无代价地进入下一个阶段，并且这个选择是不可逆的，因此我们用边权为 \(0\) 的有向边作为连接两个阶段的桥梁。具体到图上，我们珂以这样操作：

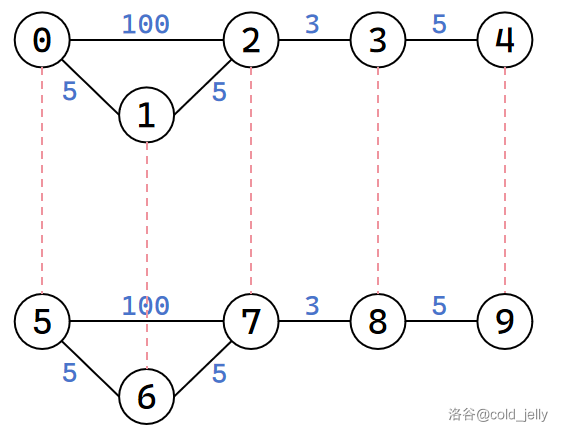
我们 copy 一份原图，节点编号在原来的基础上加 \(n\)。

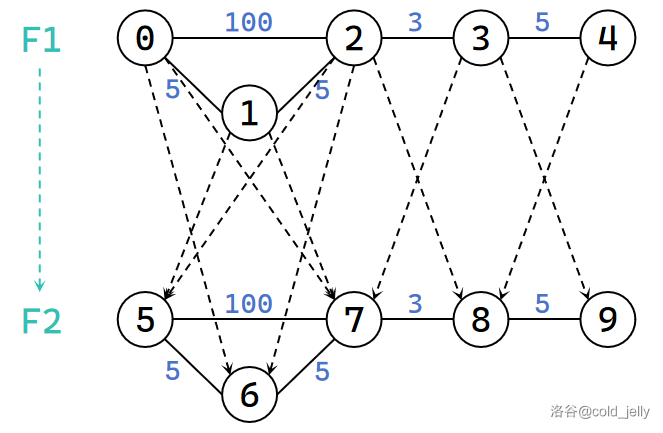
然后，如果原图上节点 \(i\) 和 \(j\) 相邻，那么增加有向边 \((i,j+n,0)\) 和 \((i+n,j,0)\)。在图上遍历时，走了边权为 \(0\) 的边，就进入到下一层图，并且不能回到上一层图，这样我们就把这个“\(0\) 元券”条件转化成图上的连边了。下图中虚线的有向边的边权为 \(0\)：

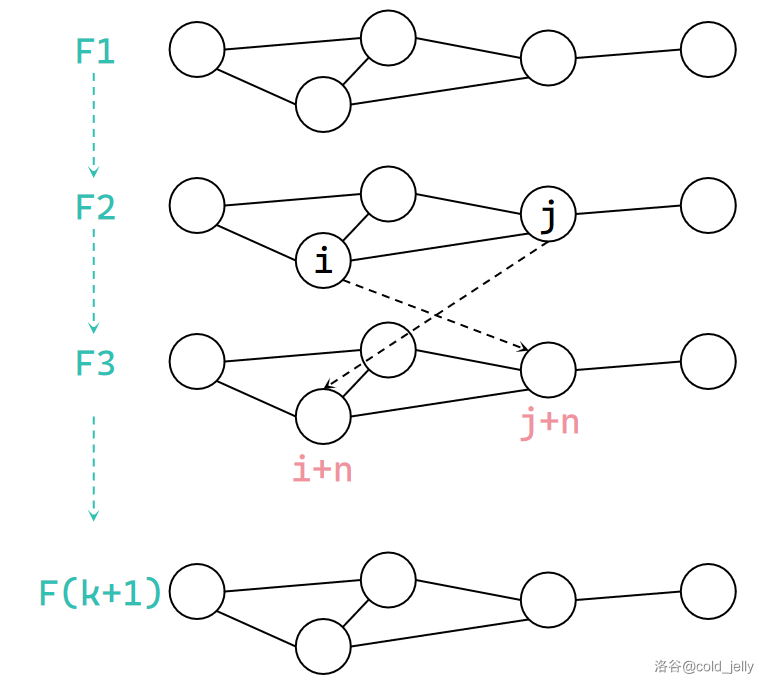
这是 \(k=1\) 时的建图方法，那当 \(k\) 更大时呢？此时我们珂以将原图 copy \(k\) 份，形成 \(k+1\) 层图，然后对于相邻两层图之间按照 \((i,j+n,0),(i+n,j,0)\) 的规律建立有向边。第 \(i\) 层到第 \(i+1\) 层的边权为 \(0\) 的有向边代表进入下一阶段。最终我们在跑最短路时经过了多少条有向边就代表我们使用了几次“\(0\) 元券”机会。

这里有几个需要注意的点：

1. 假设我们要求的最短路起点为 \(s\)，终点为 \(t\)，那么我们默认起点就是 \(s\) 在原图的位置，而终点不唯一，可以是 \(t+\lambda n(\lambda\in[0,k])\) 这 \(k+1\) 个点中的任意一个（这里 \(\lambda\) 代表我们用了几次机会），因此我们实际要求的答案是 \(\displaystyle \min_{\lambda\in[0,k]}\{dist(s,t+\lambda n)\}\)；
2. 由于我们实际有 \(k+1\) 层图，因此空间要开到 \(k+1\) 倍。

在建完图后，我们再用 Dijkstra 算法跑单源最短路即可。

#include<bits/stdc++.h>
#define PII pair<int, int>
using namespace std;
const int N = 1e4 + 10, K = 10, INF = 1e9;
int n, m, k, s, t, ans = INF;
vector<PII> e[N * (K + 1)];
int dist[N * (K + 1)];
bool st[N * (K + 1)];
void dijkstra(int s)
{
	priority_queue<PII> q;
	for(int i = 0; i < N * (K + 1); i ++) dist[i] = INF;
	dist[s] = 0;
	q.push({0, s});
	while(q.size())
	{
		int u = q.top().second;
		q.pop();
		if(st[u]) continue;
		st[u] = true;
		for(auto i : e[u])
		{
			int v = i.second, w = i.first;
			if(dist[v] > dist[u] + w)
			{
				dist[v] = dist[u] + w;
				q.push({-dist[v], v});
			}
		}
	}
}
signed main()
{
	cin >> n >> m >> k >> s >> t;
	for(int i = 1; i <= m; i ++)
	{
		int u, v, w;
		scanf("%d%d%d", &u, &v, &w);
		e[u].push_back({w, v});
		e[v].push_back({w, u});
		for(int j = 0; j < k; j ++)
		{
			e[u + j * n].push_back({0, v + (j + 1) * n});
			e[v + j * n].push_back({0, u + (j + 1) * n});
			e[u + (j + 1) * n].push_back({w, v + (j + 1) * n});
			e[v + (j + 1) * n].push_back({w, u + (j + 1) * n});
		}
	}
	dijkstra(s);
	for(int i = 0; i <= k; i ++)
		ans = min(ans, dist[t + i * n]);
	cout << ans;
	return 0;
}

---

例题 \(2\)：P4822 [BJWC2012] 冻结：在普通单源最短路问题的基础上添加了 \(k\) 次“半价”机会。

其实就是双倍经验，在建图时把 \(0\) 边权改为 \(\dfrac{w}{2}\) 就可以了。

---

例题 \(3\)：P3119 [USACO15JAN] Grass Cownoisseur G。

这道题先给定一张有向图，然后从节点 \(1\) 出发，在跑的中途有 \(1\) 次珂以选择逆向跑，问最后回到 \(1\) 的所有路径中经过不同节点个数的最大值。

此题我们依然考虑建分层图，考虑如何刻画“逆向跑”。假设对于有向边 \((i,j)\)，我们在逆向跑完后就没有机会了，这时就应该进入下一层（下一个阶段）。因此我们可以连有向边 \((j,i+n)\)，这样我们经过这条边时就相当于使用机会。

建好图后，跑 Tarjan 求强联通分量的板子再缩点求解即可。