【图论】总结 1：单源最短路问题

前置知识：图的基本概念、图的存储、图的遍历。

注 \(1\)：以下对于图 \(G=(V,E)\)，统一用 \(n=|V|\) 表示点数、\(m=|E|\) 表示边数，且默认 \(G\) 中节点按照 \([1,n]\) 编号。

注 \(2\)：函数 \(dist(i,j)\) 表示节点 \(i\) 到 \(j\) 的最短路径长度，规定 \(i\) 与 \(j\) 不连通（或不可达）时 \(dist(i,j)=+\infty\)，规定 \(dist(i,i)=0\)。

注 \(3\)：对于 \(i\) 到 \(j\) 的边权为 \(w\) 的有向边，我们用三元组 \((i,j,w)\) 表示。并记函数 \(w(i,j)\) 表示这里的边权 \(w\)。

单源最短路问题就是求一张图上一个固定点到其余点的最短路径的长度的问题。

下图描述了有向图 \(G\) 中节点 \(1\) 到节点 \(4\) 的最短路径（边上数字代表边权），则有 \(dist(1,4)=7\)：

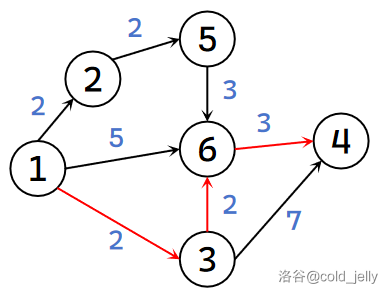
我们以求起点 \(1\) 到其余点的最短路径的长度的问题为例，故令 \(dist(i)\) 表示 \(dist(1,i)\)。

Dijkstra 算法

Dijkstra 算法是一种基于贪心思想实现求解单源最短路问题的算法。算法流程如下：

初始时，\(dist(1)=0\)，并由于其它节点还未被访问（我们此时假定它们与 \(1\) 号节点均不连通），令 \(dist(i)=+\infty(i\ne 1)\)，然后令与 \(1\) 号节点相邻的节点的 \(dist\) 值为边权；
找到一个未被标记的且 \(dist\) 值最小的节点 \(u\)，标记 \(u\)；
扫描 \(u\) 的所有出边 \((u,v,w)\)，如果 \(dist(v)>dist(u)+w\)，则更新 \(dist(v)=dist(u)+w\)；
重复步骤二三，到所有点被标记时结束算法。

以上面的例子为例，下图为初始状态：

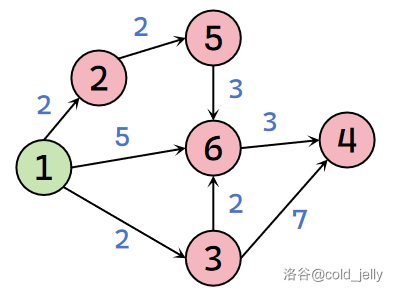
此时除 \(dist(1)=0\)，其余点 \(dist\) 值均为 \(+\infty\)。

与 \(1\) 号节点相邻的节点有 \(\{2,3,6\}\)，故令 \(dist(2)=2,dist(3)=2,dist(6)=5\)，其余点保持不变。其中未被标记的且 \(dist\) 值最小的是 \(2\) 号节点（\(3\) 号节点也可以，取决于枚举顺序，我这里就默认编号较小的优先啦），故标记 \(2\) 号节点。此时扫描 \(2\) 号节点全部出边：

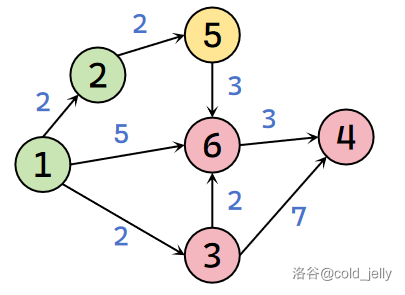
因为 \(dist(5)=+\infty>dist(2)+w(2,5)=4\)，故更新 \(dist(5)=4\)。此时未被标记的点是 \(\{3,4,5,6\}\)（注意这里 \(5\) 号节点未被标记）。未被标记的点里 \(dist(3)=2\) 最小，故标记 \(3\) 号节点，并扫描其全部出边：

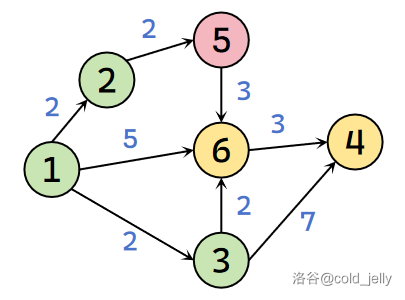
对于 \(6\) 号节点，\(dist(6)=5>dist(3)+w(3,6)=4\)，故更新 \(dist(6)=4\)；

对于 \(4\) 号节点，\(dist(4)=+\infty>dist(3)+w(3,4)=9\)，故更新 \(dist(4)=9\)。

此时未被标记的点是 \(\{4,5,6\}\)，其中 \(dist(5)=4\) 最小，故标记 \(5\) 号节点，扫描全部出边：

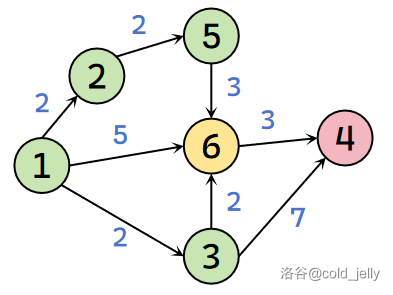
因为 \(dist(6)=4<dist(5)+w(5,6)=7\)，故不更新。此时未被标记的点是 \(\{4,6\}\)，其中 \(dist(6)=4\) 最小，故标记 \(6\) 号节点，扫描全部出边：

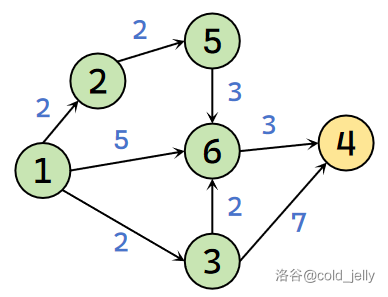
因为 \(dist(4)=9>dist(6)+w(4,6)=7\)，故更新 \(dist(4)=7\)。此时剩下未被标记的点就只有 \(4\) 了，将它标记之后所有点都已被标记，此时结束算法。最终我们求得了所有点的 \(dist\) 值。

Dijkstra 算法只适用于非负权图的最短路问题的求解，因为只有当边权均非负时才能保证贪心的正确性。详细证明可以参考 link，这里就不展开啦。

按照上述流程，不难写出 Dijkstra 算法的代码。且我们可知朴素 Dijkstra 算法的时间复杂度是 \(O(n^2)\) 的，算法仍不够优秀，因此考虑优化。算法瓶颈在于寻找最小 \(dist\) 值的过程，而 \(dist\) 恰好可以用堆来维护，并用 \(O(\log n)\) 的时间删除及询问最小值、或更新一条边。计算可知用堆优化的 Dijkstra 算法的时间复杂度为 \(O((m+n)\log n)\)，通常能够较为高效地处理 \(10^5\) 级别的题目。

堆优化的 Dijkstra 算法的模板代码如下：

#include<bits/stdc++.h>
#define PII pair<int, int>
using namespace std;
const int N = 1e5 + 10, M = 5e5 + 10, INF = 1e9;
int n, m;
vector<PII> e[N];
int dist[N];//dist[i] = dist(s, i)
bool st[N];//标记数组 
void dijkstra(int s)//s 为起始点 
{
	priority_queue<PII> q;//大根堆，second 为编号 
	for(int i = 1; i <= n; i ++) dist[i] = INF;
	dist[s] = 0;
	q.push({0, s});
	while(q.size())
	{
		int u = q.top().second;
		q.pop();
		if(st[u]) continue;
		st[u] = true;
		for(auto i : e[u])//扫描全部出边 
		{
			int v = i.second, w = i.first;
			if(dist[v] > dist[u] + w)//更新 
			{
				dist[v] = dist[u] + w;
				q.push({-dist[v], v});
			}
		}
	}
}
int main()
{
	cin >> n >> m;
	for(int i = 1; i <= m; i ++)
	{
		int u, v, w;
		scanf("%d%d%d", &u, &v, &w);
		e[u].push_back({w, v});
	}
	dijkstra(1);
	for(int i = 1; i <= n; i ++) printf("%d\n", dist[i]);
	return 0;
}

Bellman-Ford 算法

Bellman-Ford 算法基于迭代思想，其可以解决带有负权边的图上的最短路问题，并能判断是否存在最短路径。

首先要明白一个结论：如果对于 \(G=(V,E)\)，\(\forall e=(u,v,w)\in E,\text{st. }dist(v)\le dist(u)+w\)，那么 \(dist\) 即为我们要求的最短路径长度。因此 Bellman-Ford 算法的核心就是通过某种操作，使得所有不满足 \(dist(v)\le dist(u)+w\) 的边 \((u,v,w)\) 变得符合条件。

我们扫描所有边 \((u,v,w)\)，如果 \(dist(v)>dist(u)+w\)，则令 \(dist(v)=dist(u)+w\)，反复执行 \(n-1\) 轮就可以了，这样我们便可以用 \(O(nm)\) 的时间求得 \(dist\)。

可以发现这个操作与 Dijkstra 算法里的一步长得一样，我们把这个操作叫做松弛（relax）操作。

值得注意的是，当图中存在负环（就是边权和为负数的环）时，由于我们可以在负环上不停地跑来使得路径长度无穷小，因此此时不存在最短路径，Bellman-Ford 算法在执行完 \(n-1\) 轮松弛操作后检查是否能够继续进行松弛操作，若还能则说明图中存在负环，报告无解。

Bellman-Ford 算法的实现如下：

const int N = _______, M = _______, INF = 1e9;
int n, m;
struct Edge
{
	int u, v, w;
}e[M];
int dist[N];
bool BellmanFord(int s)
{
	for(int i = 1; i <= n; i ++) dist[i] = INF;
	dist[s] = 0;
	for(int i = 1; i <= n - 1; i ++)
		for(int j = 1; j <= m; j ++)
			if(dist[e[j].v] > dist[e[j].u] + e[j].w)
				dist[e[j].v] = dist[e[j].u] + e[j].w;
	for(int i = 1; i <= m; i ++)//检查负环 
		if(dist[e[i].v] > dist[e[i].u] + e[i].w)
			return false;//无解 
	return true;
}

SPFA 算法

SPFA 本质上是用队列对 Bellman-Ford 算法进行优化的一种算法，通过减少松弛操作的执行次数从而降低复杂度。SPFA 算法的流程如下：

队列初始只包含起点 \(1\)，并令 \(dist(1)=0\)，其余点 \(dist\) 为 \(+\infty\)；
取出队头元素 \(u\)，扫描其所有出边 \((u,v,w)\)（其中 \(v\) 未被标记），若 \(dist(v)>dist(u)+w\)，则令 \(dist(v)=dist(u)+w\)，同时如果 \(v\) 不在队列中，就将其入队，依次反复进行，直到队列为空。

在随机图上，可以证明 SPFA 算法的时间复杂度为 \(O(km)\)，其中 \(k\) 是一个较小常数，因此 SPFA 算法在大多数情况下跑得很快。但是在特殊构造的图（例如菊花图、网格图等）上效率将退化为 \(O(nm)\)，因此如果图中没有负权边时尽量还是用 Dijkstra 算法。

我们以下面这张无向图为例，初始时 \(1\) 号节点被压入队列 \(q\)，且 \(dist(1)=0\)：

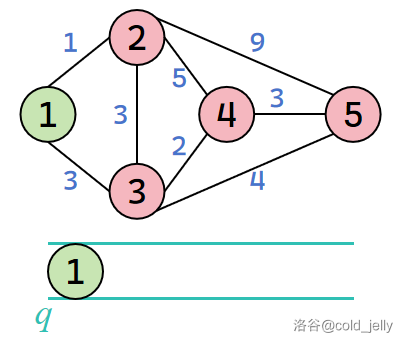
取出队头元素 \(1\)，扫描 \(1\) 号节点全部出边：

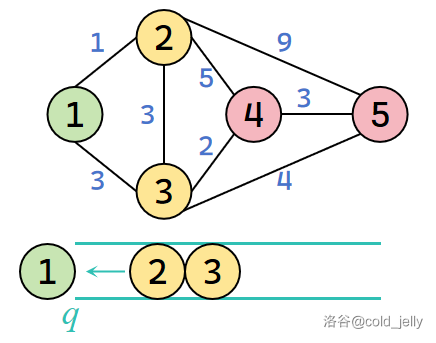
对于 \(2\) 号节点，\(dist(2)=+\infty>dist(1)+w(1,2)=1\)，故更新 \(dist(2)=1\)，并将 \(2\) 入队；对于 \(3\) 号节点，\(dist(3)=+\infty>dist(1)+w(1,3)=3\)，故更新 \(dist(3)=3\)，并将 \(3\) 入队。

然后取出队头元素 \(2\)，扫描 \(2\) 号节点全部出边：

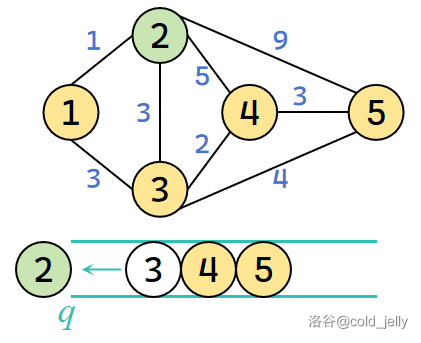
对于 \(1\) 号节点很显然不更新，不入队；\(3\) 号节点不更新，不入队；对于 \(4\) 号节点，\(dist(4)=+\infty>dist(2)+w(2,4)=6\)，故更新 \(dist(4)=6\)，并将 \(4\) 入队，\(5\) 号节点同理有 \(dist(5)=10\)，并将 \(5\) 入队。

然后取出队头元素 \(3\)，扫描 \(3\) 号节点全部出边：

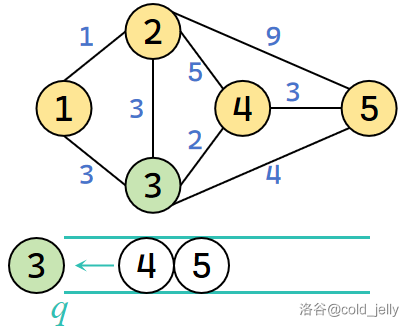
只有 \(4\) 号和 \(5\) 号节点得到更新：\(dist(4)=5,dist(5)=7\)，但由于 \(4,5\) 均在队列里，故无元素入队。

然后取出依次取出队头元素 \(4\) 和 \(5\)，发现 \(dist\) 均不更新，算法结束。

SPFA 算法代码实现如下：

#include<bits/stdc++.h>
#define PII pair<int, int>
using namespace std;
const int N = 1e5 + 10, M = 5e5 + 10, INF = 1e9;
int n, m;
vector<PII> e[N];
int dist[N];
bool st[N];//是否在队列中 
void spfa(int s)
{
	queue<int> q;
	for(int i = 1; i <= n; i ++) dist[i] = INF;
	dist[s] = 0;
	st[s] = true;
	q.push(s);
	while(q.size())
	{
		int u = q.front();
		q.pop();
		st[u] = false;//取出来就不在队列里了 
		for(auto i : e[u])
		{
			int v = i.second, w = i.first;
			if(dist[v] > dist[u] + w)//更新 
			{
				dist[v] = dist[u] + w;
				if(!st[v])//入队 
				{
					q.push(v);
					st[v] = true;
				}
			}
		}
	}
}
int main()
{
	cin >> n >> m;
	for(int i = 1; i <= m; i ++)
	{
		int u, v, w;
		scanf("%d%d%d", &u, &v, &w);
		e[u].push_back({w, v});
		e[v].push_back({w, u});
	}
	spfa(1);
	for(int i = 1; i <= n; i ++) printf("%d\n", dist[i]);
	return 0;
}

SPFA 算法同样可以处理含负权边的图上的最短路问题，同时也能判断负环的存在。具体而言，我们用 \(cnt[i]\) 记录从起点到 \(i\) 的最短路径包含的边数，松弛操作更新时顺便更新 \(cnt[v]=cnt[u]+1\)。如果发现 \(cnt[v]\ge n\)，则证明存在负环，报告无解。

posted @ 2025-07-21 20:47 cold_jelly 阅读(35) 评论(0) 收藏举报

刷新页面返回顶部

cold_jelly 的小窝

【图论】总结 1：单源最短路问题

Dijkstra 算法

Bellman-Ford 算法

SPFA 算法

公告