【字符串】总结 5：回文串和 Manacher 算法

回文串

通俗地讲，如果一个字符串正着读和反着读都一样，那么这个字符串被称为回文字符串，简称回文串。也就是说，如果字符串 \(s\) 满足：

\[\boxed{\forall i\in [1,|s|],s[i]=s[|s|-i+1]} \]

则 \(s\) 为回文串。

对于一个回文串 \(s\)，如果其长度为奇数，其被称作奇回文串，同理可定义偶回文串。对于一个回文串，如果将它比作一个轴对称图形的话，那么对称轴所在位置即为它的回文中心，而回文中心本身再加上左边所有（或右边所有）字符的长度为它的回文半径 \(R\)，因此 \(R=\left\lceil \dfrac{|s|}{2}\right\rceil\)：

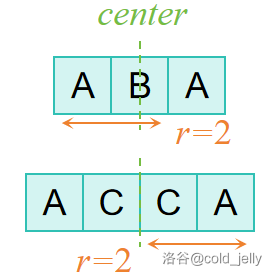
为研究方便起见，我们统一在 \(s\) 中每两个相邻字符之间插入一个不在 \(\Sigma\) 中的字符，头尾也要插（例如 #）：

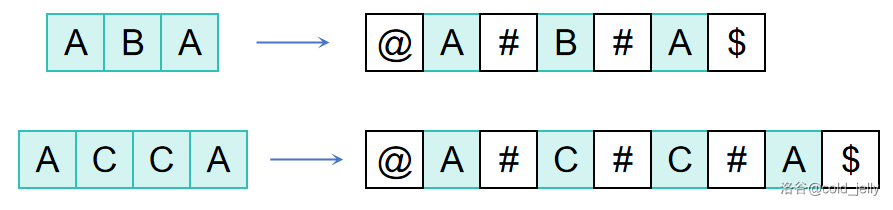
我们可以发现，做以上处理后，无论原字符串奇偶，加入 # 后的字符串都是奇回文串。

统一为奇回文串后，我们便可知若回文串的回文中心下标为 \(c\)，右端点为 \(r\)，那么 \(R=r-c+1\)。

Manacher 算法

Manacher 算法可以在 \(O(|s|)\) 的时间复杂度内求得以字符串 \(s\) 中每个字符作为回文中心的最大回文半径 \(d[i]\)。

首先考虑暴力计算，我们很容易写出如下代码：

const int N = _______;
char s[N];
int d[N];
void BF()
{
	int n = strlen(s + 1);
	for(int i = 1; i <= n; i ++)
	{
		d[i] = 1;
		while(s[i - d[i]] == s[i + d[i]]) d[i] ++;
	}
}

考虑优化，也就是利用已知的 \(d\) 值求得未知的 \(d\) 值。

不妨假设我们已经知道了 \(i\in[1,a-1]\) 的 \(d[i]\) 值，现在要求 \(d[a]\)。我们可以利用回文本身具有的对称性质快速计算 \(d[a]\)。如果我们在之前求 \(d[i]\) 的过程中已经拓展过 \(a\) 这个位置，那前面就一定有和当前的字符对称的内容，那该字符显然也会拥有前面与它对称的字符的回文半径。

例如 \(s=\text{ABACABA}\)，我们已经求得了 \(d[1]\sim d[5]\)，我们发现 \(6\) 这个位置在之前求 \(d[4]\) 时就已经被拓展过了：

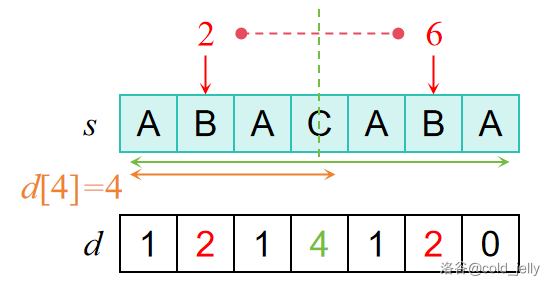
我们知道中点公式：\(m=\dfrac{l+r}{2}\)，可推知 \(l=2m-r\)，对应到字符串中即就是已知回文中心 \(m=c\)，又已知 \(r=a\)，那么对称点下标为 \(2m-r=2c-a\)。也就是说 \(d[6]\) 可以在 \(d[2\times 4-6]=d[2]=2\) 的基础上拓展，也就是 \(d[6]\) 可以从 \(3\) 开始拓展继续求，因为其回文半径至少为 \(d[2]=2\)。此外，还要在 \(r=a\) 及以内的可以扩展的最长长度取最小值。

也就是说，之前已经拓展过 \(i\) 位置的回文串的回文中心下标为 \(c\)，其右端点为 \(r\)，那么我们可知：

\[\boxed{d[i]=\min\{d[2c-r],r-i+1\}} \]

然后在此基础上接着拓展即可。

按此思路，我们可以实现线性求 \(d\) 数组的代码：

const int N = _______;
char org[N], s[N * 2];
int n;
int d[N];
void init()//预处理 
{
//	org 为原串 
	int cur = 0;
	s[0] = '@', s[++ cur] = '#';
	for(int i = 1; i <= n; i ++)
	{
		s[++ cur] = org[i];
		s[++ cur] = '#';
	}
	s[++ cur] = '$';
	n = cur - 1;
}
void Manacher()
{
	init();
	int c = 0, r = 0;//回文中心以及右端点 
	for(int i = 1; i <= n; i ++)
	{
		if(i > r) d[i] = 1;
		else d[i] = min(d[c * 2 - i], r - i + 1);
		while(s[i - d[i]] == s[i + d[i]]) d[i] ++;//拓展 
		if(i + d[i] - 1 > r) c = i, r = i + d[i] - 1;//更新 c, r 
	}
}

代码中头尾分别加上 @ 和 $ 字符是为了防止越界。

模板题

求最长回文子串的长度：P3805 【模板】manacher，用 Manacher 算法求出 \(d\) 数组后答案就很好求了。