【字符串】总结 4：扩展 KMP

\(z\) 函数

对于字符串 \(s\)（下标从 \(0\) 开始），定义 \(z\) 函数 \(z(i)\) 的值为 \(s\) 与 \(s[i\sim |s|-1]\) 的最长公共前缀的长度，并且规定 \(z(0)=0\)。例如对于 \(s=\text{ABAAABC}\)：

• \(z(0)\)：由规定，值为 \(0\)。
• \(z(1)\)：\(s\) 与 \(\text{BAAABC}\) 无公共前缀，值为 \(0\)；
• \(z(2)\)：\(s\) 与 \(\text{AAABC}\) 的最长公共前缀为 \(\text{A}\)，故值为 \(1\)；
• \(z(3)\)：\(s\) 与 \(\text{AABC}\) 的最长公共前缀为 \(\text{A}\)，故值为 \(1\)；
• \(z(4)\)：\(s\) 与 \(\text{ABC}\) 的最长公共前缀为 \(\text{AB}\)，故值为 \(2\)；
• \(z(5),z(6)\)：无公共前缀，值为 \(0\)。

根据定义，我们很容易可以写出 \(O(|s|^2)\) 的求 \(z\) 函数的代码：

const int N = _______;
char s[N];
int z[N];
void getz()
{
	int n = strlen(s);
	for(int i = 0; i < n; i ++)
		while(i + z[i] - 1 < n && s[z[i]] == s[i + z[i]]) z[i] ++;
}

线性复杂度求 \(z\) 函数（扩展 KMP）

我们注意到，while(i + z[i] - 1 < n && s[z[i]] == s[i + z[i]]) z[i] ++; 一句是通过枚举实现的 \(O(|s|)\) 做法，因此考虑优化。

根据 \(z\) 函数的定义，我们知道 \(z(i)\) 是满足 \(s[0\sim k-1]=s[i\sim i+k-1]\) 的最大的 \(k\) 值，因此我们可以得到 \(z\) 函数的一条性质：

\[\boxed{\forall l\in[0,z(i)-1],r\in[i,i+z(i)-1],\text{st. }s[l\sim r]=s[l-i\sim r-i]} \]

按照 KMP 算法求 \(nxt\) 数组的思路，我们可以用已知的 \(z\) 函数值求出未知的 \(z\) 函数值，如果不行再枚举。

不妨记录 \(i+z(i)-1\) 的最大值 \(r\)，此时 \(l\) 就是 \(r\) 下对应的 \(i\) 这个下标：

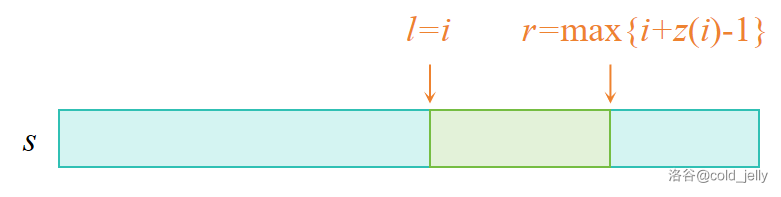
那么根据上面的性质，对于位置 \(j\le r\)，有 \(s[j\sim r]=s[j-l\sim r-l]\)：

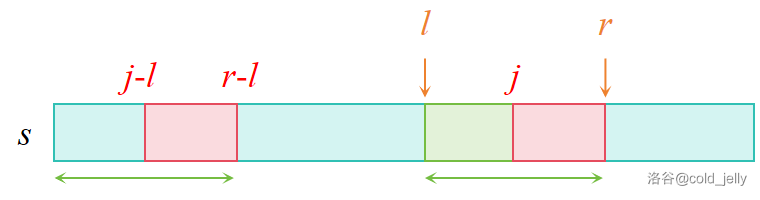
所以 \(z(j)\) 有两种情况：

• 与 \(z(j-l)\) 一样，即 \(z(j)=z(j-l)\)；
• 要么 \(j\) 这个位置可以匹配完整个 \(r-j+1\)，还可以继续向后匹配。

即就是：\(z(j)\ge \min\{z(j-l),r-j+1\}\)。

如果此时有 \(z(j-l)<r-j+1\)，那么我们选择直接继承 \(z(j-l)\)：

if(z[j - l] < r - j + 1) z[j] = z[j - l];

否则其还可以向后匹配：

if(z[j - l] > r - j + 1)
{
	z[j] = r - j + 1;
	while(j + z[j] - 1 < n && s[z[j]] == s[j + z[j]]) z[j] ++;
}

还有一些细节，例如当 \(j>r\) 时，需要直接暴力匹配。而在每次暴力匹配后都应更新 \(l\) 和 \(r\) 的值。因此可以写出完整的线性求 \(z\) 函数的代码（为统一马蜂，以下代码用 i 代替上述 \(j\)）：

const int N = _______;
char s[N];
int z[N];
void getz()
{
	int n = strlen(s);
	int l = 0, r = 0;//初始 l, r 均为 0 
	for(int i = 1; i < n; i ++)
	{
		if(i <= r && z[i - l] < r - i + 1) z[i] = z[i - l];
		else
		{
			z[i] = max(0, r - i + 1);
			while(i + z[i] - 1 < n && s[z[i]] == s[i + z[i]]) z[i] ++;
			if(r < i + z[i] - 1) l = r, r = i + z[i] - 1;//更新 l, r 
		}
	}
}

以上算法就是扩展 KMP 算法了。

模板题

P5410 【模板】扩展 KMP/exKMP（Z 函数）