【FHQ-Treap】学习笔记
前置知识:BST & Treap
模板题 1:P3369 【模板】普通平衡树;
模板题 2:P3391 【模板】文艺平衡树。
简介
Treap 是一种入门级平衡树,有旋 Treap 通过旋转操作维持其平衡。相应地,无旋 Treap 不需要通过旋转,而是利用分裂与合并操作来维持平衡。由于创始人的名字,无旋 Treap 又习惯称作 FHQ-Treap。
在阅读前,需要说明的一点是,在 FHQ-Treap 中,对于重复数值,我们不再像有旋 Treap 那样记录 \(cnt\),而是直接当作不同节点来存。
FHQ-Treap 的分裂操作
一棵 Treap 实际上维护了一个特定权值 \(key\) 序列 \([l,r]\),中序遍历得到的权值序列是单调不减的。在此基础上,我们先看分裂操作的原理。
不妨假设我们给定值 \(k\),想要将一棵 Treap 按节点 \(key\) 值分成小于等于 \(k\) 以及大于 \(k\) 的两部分,实际上就相当于把这棵 Treap 维护的 \(key\) 值序列分成了 \([l,k]\) 和 \([k+1,r]\) 两部分,也就是把一棵大 Treap 分裂成了两棵小 Treap。
总的来说,一棵 Treap 相当于一个区间,分裂等同于拆区间。于是我们考虑如何拆。
我们结合图示来分析。
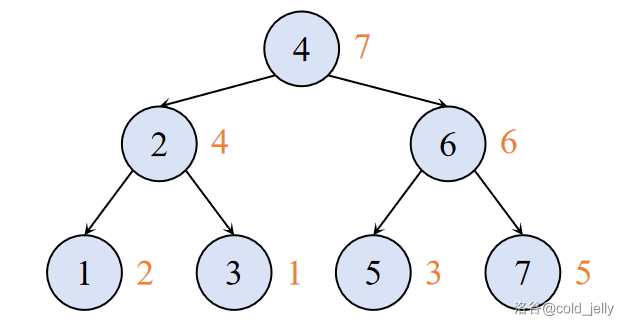
上图展示了一棵 Treap,其中节点内部数值代表 BST 权值 \(key\),节点外橙色数值代表大根堆权值 \(val\)(该权值是随机的),现在我们按照 \(k=5\) 来进行分裂。
为方便起见,我们将维护序列 \([l,k]\) 及 \([k+1,r]\) 的小 Treap 分别称作左区间树及右区间树。我们首先建立两个虚拟节点分别作为两区间树的根节点,如下图中虚线点所示:
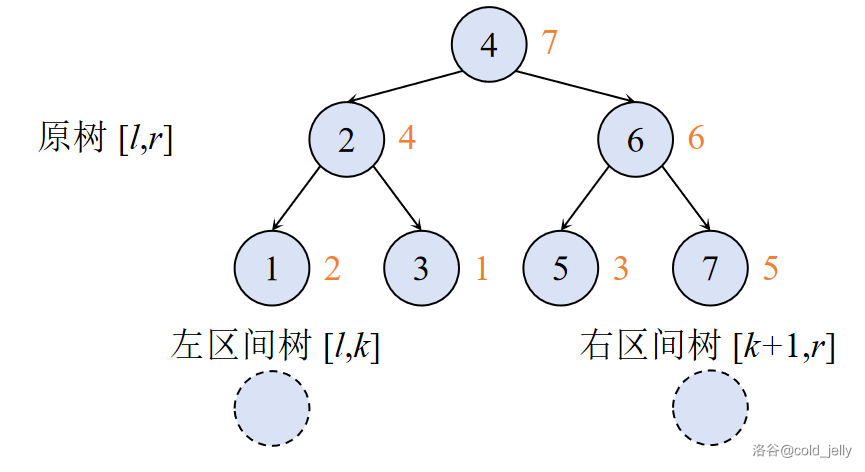
接着我们遍历原树。如果当前访问到的节点 \(u\) 的 \(key\) 值小于等于 \(k\),则该节点与其左子树里的所有节点都应该归入左区间树,此时我们应将左区间树上一个虚拟节点赋为 \(u\),然后给 \(u\) 以一个虚拟的右儿子;反之若节点 \(u\) 的 \(key\) 值大于 \(k\),则该节点与其右子树里的所有节点都应该归入右区间树,此时我们应将右区间树上一个虚拟节点赋为 \(u\),然后给 \(u\) 以一个虚拟的左儿子;如果 \(u\) 为空,则将左右区间树的虚拟节点赋为 \(0\)。这种建树方式保证了生成的左右区间树仍保持 BST 性质与大根堆性质。
例如,上述操作步骤用图示可分布表示为(深蓝色节点表示已被遍历):
第一步:
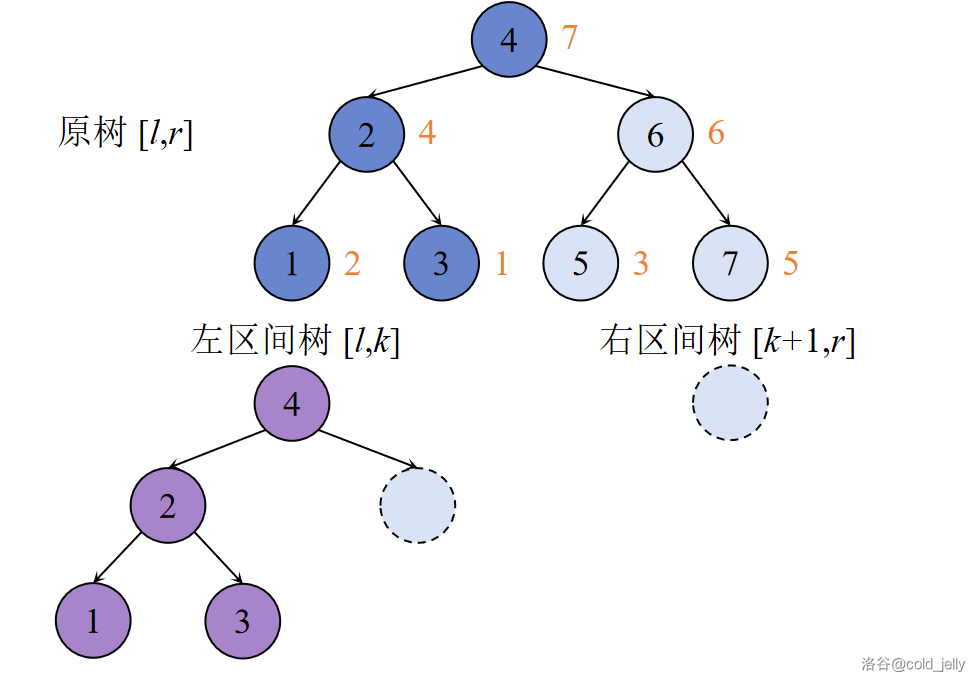
第二步:
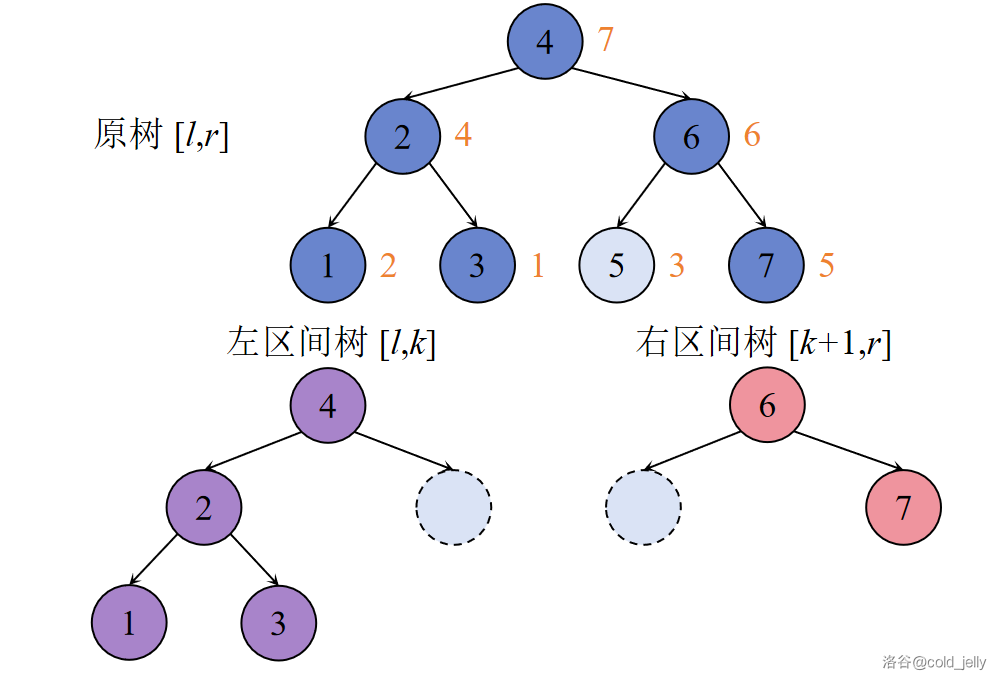
第三步:
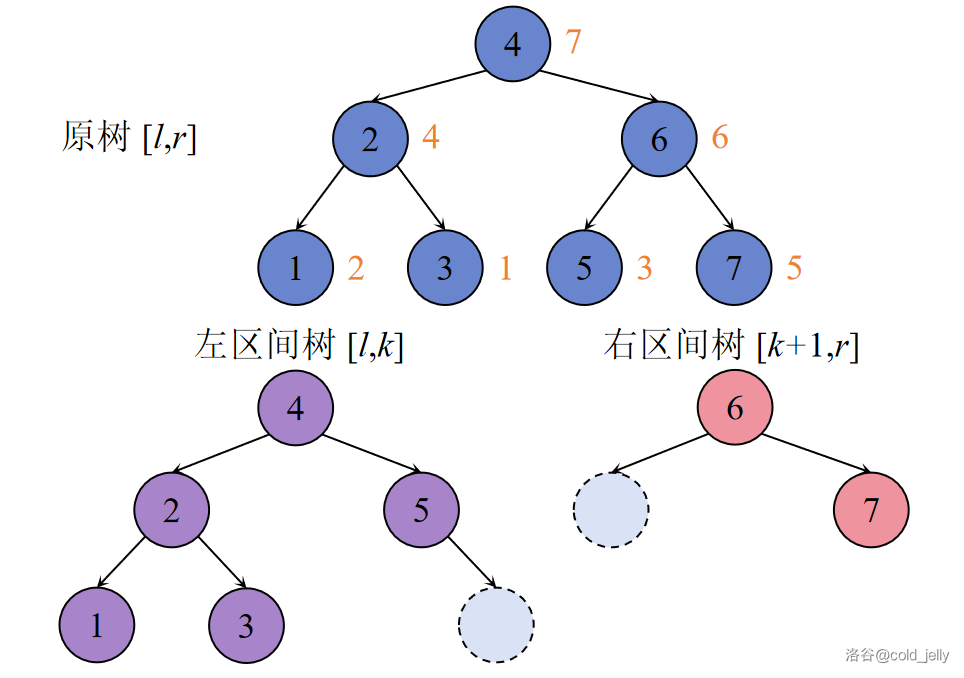
第四步:
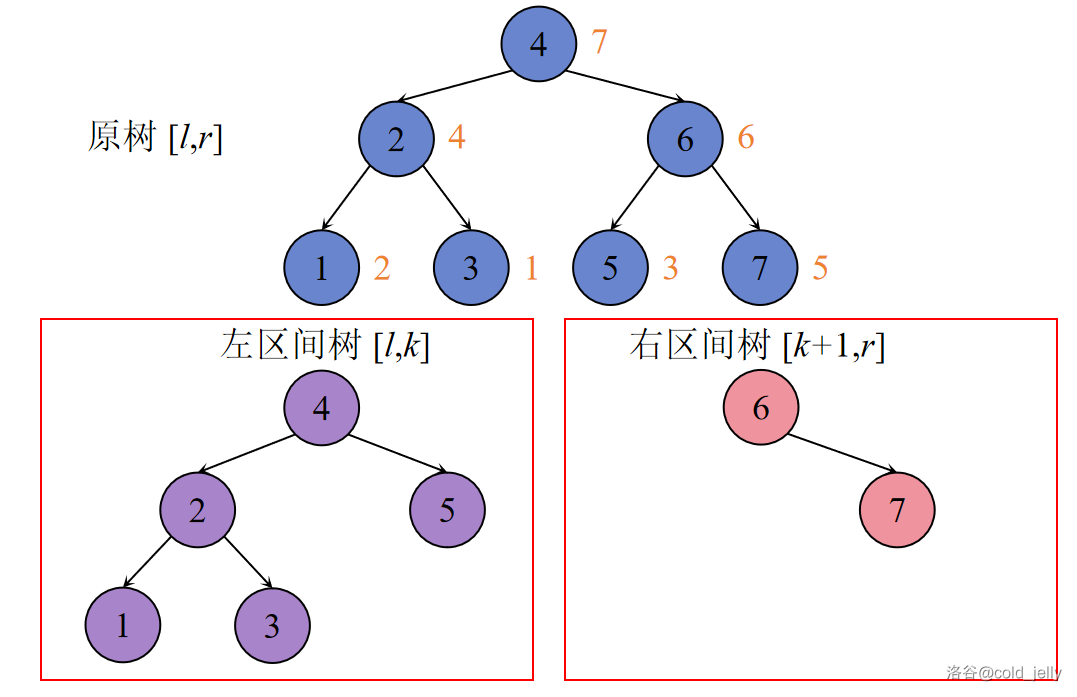
我们就完成了分裂操作。
因为每访问到一个非空的 \(u\) 节点时,递归分裂子树进行的操作会改变左右儿子,所以在维护一些值如子树大小的时候需要用同线段树类似的方法进行上传操作。
上传操作代码如下:
void pushup(int u)//上传信息,类似线段树
{
tr[u].siz = tr[tr[u].l].siz + tr[tr[u].r].siz + 1;
}
然后我们就可以完成分裂操作(split)的代码了:
void split(int u, int k, int &x, int &y)//分裂区间为 [l, k] 和 [k + 1, r],x 和 y 为虚拟节点
{
if(!u)//当前节点为空节点,虚拟节点赋 0 处理
{
x = y = 0;
return;
}
if(tr[u].key <= k)
{
x = u;//在左区间树中对右儿子建立虚拟节点
split(tr[u].r, k, tr[u].r, y);//继续分裂右子树
}
else
{
y = u;//在右区间树中对左儿子建立虚拟节点
split(tr[u].l, k, x, tr[u].l);//继续分裂左子树
}
pushup(u);
}
在外部调用时,直接给出 \(x\) 和 \(y\) 就行了。
split(root, k, x, y);//分裂 [l, r]
//or
split(root, qr, x, z);//分裂 [l, r] 中的 [ql, qr],按照拆区间的方法拆为 [l, qr] 和[qr + 1, r],x 为左区间树的根节点,z 为右区间树的根节点
split(x, ql - 1, x, y);//再将 [l, qr] 分成 [l,ql-1] 和 [ql, qr],此时 y 就是 [ql, qr] 区间树的根节点
除了按照 \(key\) 值分裂,我们还可以以排名 \(rank\) 分裂,并将其应用于序列操作。
具体而言,假设我们以排名为 \(k\) 为界划分整个序列 \([l, r]\) 为 \([l,k]\) 和 \([k+1,r]\)。我们依然给左右区间树以一个虚拟的根节点,然后在遍历的时候进行分类讨论:
- 若当前节点 \(u\) 为空节点,则将左右区间树虚拟节点赋 \(0\);
- 否则如果 \(u\) 的左子树大小加上 \(u\) 节点小于等于 \(k\),说明排名 \(k\) 的节点在右子树,递归分裂右子树;
- 否则说明排名 \(k\) 的节点在左子树,递归分裂左子树。
可以结合代码食用:
void split(int u, int k, int &x, int &y)//分裂区间为 [l, k] 和 (k, r],x 和 y 为虚拟节点
{
if(!u)//当前节点为空节点,虚拟节点赋 0 处理
{
x = y = 0;
return;
}
if(tr[tr[u].l].siz + 1 <= k)//分裂右子树
{
x = u;
split(tr[u].r, k - tr[tr[u].l].siz - 1, tr[u].r, y);
}
else//分裂左子树
{
y = u;
split(tr[u].l, k, x, tr[u].l);
}
pushup(u);
}
FHQ-Treap 的合并操作
同分裂操作的分析,我们来讲讲 FHQ-Treap 如何合并。
合并是分裂的逆过程,Treap 合并其实就是将两棵小 Treap 合为一棵大 Treap,也就是把小区间合并为大区间的过程。注意,合并的左区间树与右区间树不能存在区间相交或顺序颠倒的情况,例如,如果左区间树的 \(val\) 范围为 \([3,6]\) 而右区间树的 \(val\) 范围为 \([5,7]\),那么我们发现它们的 \(val\) 值范围是相交的,或者右区间树的 \(val\) 比左区间树小,在遍历时我们就没有很好的办法使其满足 Treap 的性质。
我们还是根据图示来理解合并操作,以上一节中分裂得到的两棵 Treap 为例。
先展示图片(深色节点表示已被访问,浅色节点表示未被访问,节点内部数值为 \(key\),外部橙色数值为大根堆的随机 \(val\)):
原始情境:
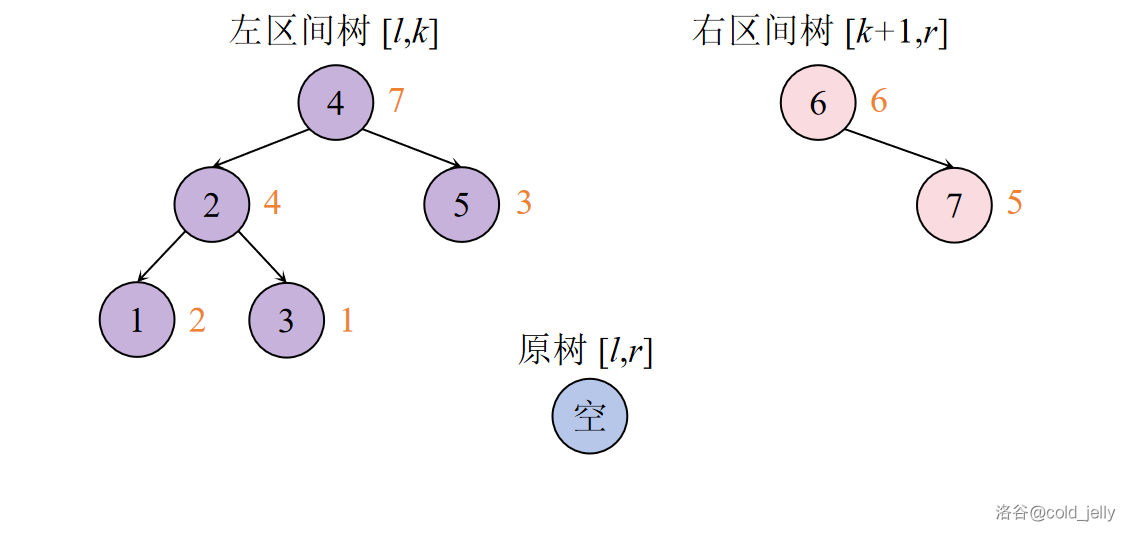
第一步:
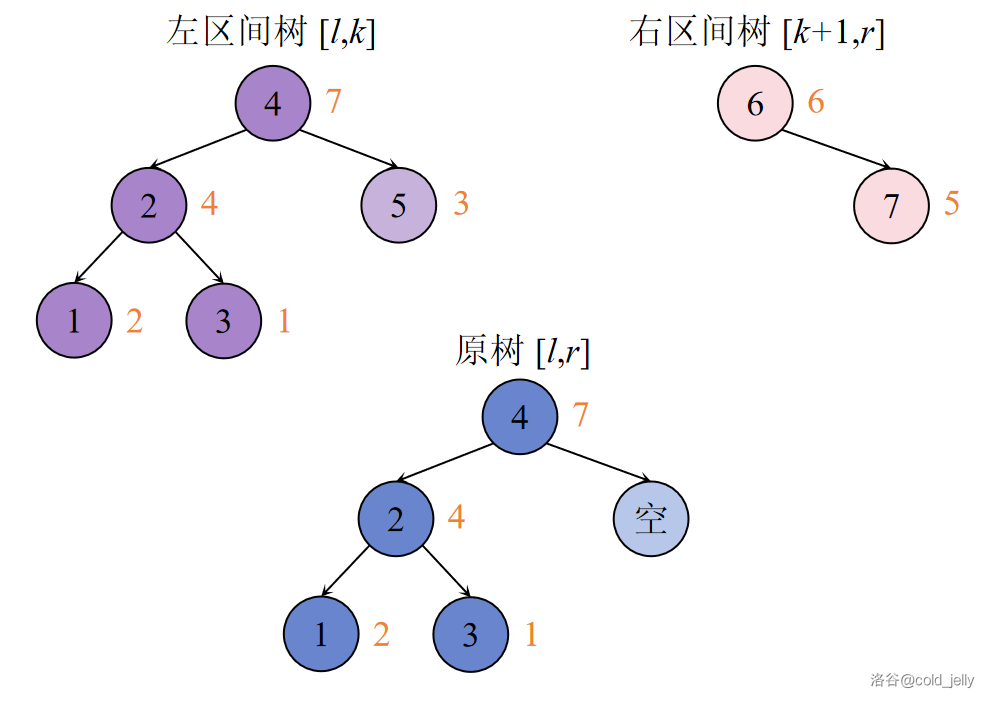
第二步:
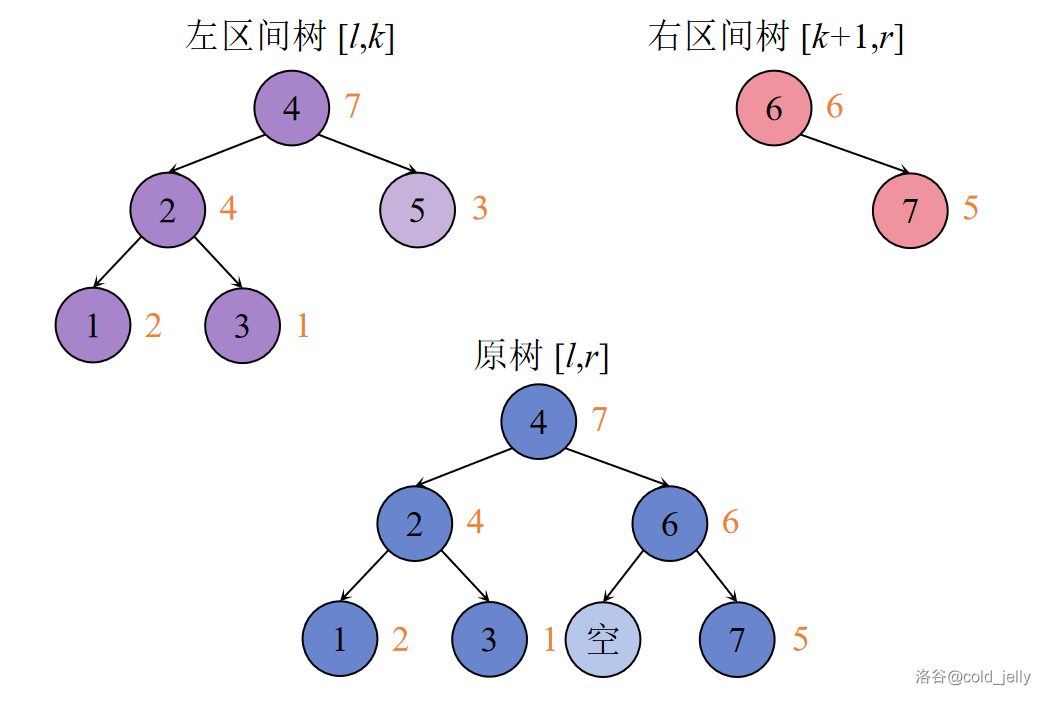
第三步:
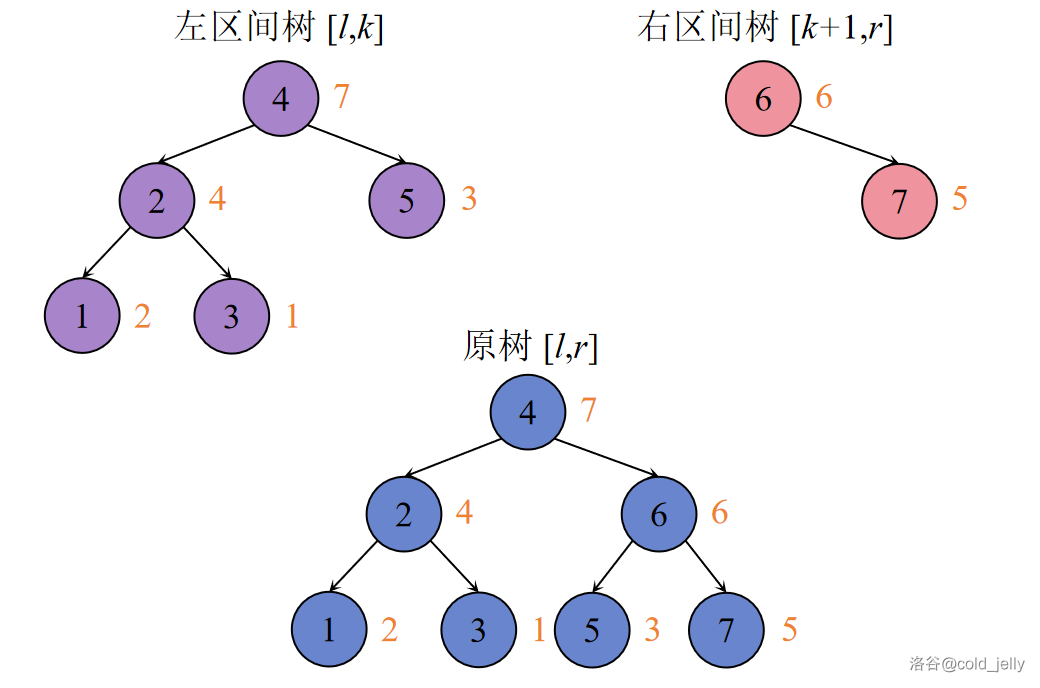
我们发现,假设合并前两区间树的根节点为 \(u\) 和 \(v\),那么如果要么 \(u\) 及其子树在 \(v\) 的左子树中,要么 \(v\) 及其子树在 \(u\) 的右子树中,就可以保证合并后的树仍具有 BST 性质。
接下来考虑如何使合并后的树具有大根堆性质。在刚刚的方案基础上,因为要么 \(u\) 是 \(v\) 的父节点、要么 \(v\) 是 \(u\) 的父节点,根据大根堆的性质,那么就要保证让 \(val\) 值大的为父节点。我们需要在第一种情况中将 \(u\) 的右子树与 \(v\) 及其子树继续合并,在第二种情况中将 \(u\) 及其子树与 \(v\) 的左子树继续合并。若 \(u\) 或 \(v\) 中任意一个点为空节点时,则非空节点为根。
根据这一操作步骤,我们可以写出合并的代码:
int merge(int u, int v)//合并两个以 u 和以 v 为根的树
{
if(!u) return v;
if(!v) return u;
pushdown(u), pushdown(v);
if(tr[u].val > tr[v].val)//u 为根
{
tr[u].r = merge(tr[u].r, v);//继续合并
pushup(u);
return u;//返回根
}
else//v 为根
{
tr[v].l = merge(u, tr[v].l);//继续合并
pushup(v);
return v;//返回根
}
}
至此,FHQ-Treap 最重要的两个操作就讲完了,FHQ-Treap 就用这两个操作维护其平衡的。
FHQ-Treap 的插入、删除与查询操作
基于分裂和合并操作,我们可以实现 FHQ-Treap 的各种操作。
与有旋 Treap 一样,我们依然要额外储存根节点信息与编号:
int root;//根节点
int idx;//当前已经分配到了第 idx 个节点
FHQ-Treap 的新建节点操作也与有旋 Treap 一致:
int create(int key)//新建 BST 权值为 key 的节点
{
tr[++ idx].key = key;
tr[idx].val = rand();
tr[idx].siz = 1;
return idx;
}
对于插入操作(insert),例如插入 BST 权值为 \(k\) 的节点,我们实际上可以把它理解为先按 \(k\) 把原树分裂为两区间树,把新加节点看作右区间树与左区间树合并,再与右区间树合并:
void insert(int key)
{
split(root, key, x, y);
root = merge(merge(x, create(key)), y);
}
对于单点删除(remove),例如删除一个 BST 权值为 \(k\) 的节点,我们可以将原树分裂为 \([l,k-1]\)、\([k,k]\)、\([k+1,r]\) 三个区间,然后将 \([k,k]\) 的左右儿子合并,这样这棵树的根节点就被删除了,然后再将三棵树合并即可删除节点了:
void remove(int key)
{
split(root, key - 1, x, y);
split(y, key, y, z);
y = merge(tr[y].l, tr[y].r);
root = merge(merge(x, y), z);
}
给定数值 \(key\),如何查找其在 Treap 中的排名呢?
按权值分裂,那么查询给定权值的排名即为查询小于给定权值的数的个数 \(+1\),分裂即可:
int qrank(int key)//查询数值 key 排名
{
split(root, key - 1, x, y);
int res = tr[x].siz + 1;
root = merge(x, y);
return res;
}
给定排名 \(rank\),如何查找对应的权值呢?
考虑在 FHQ-Treap 上从根节点开始跳,对于当前遍历到的节点 \(u\) 分类讨论:
- 若 \(u\) 的左子树大小 \(+1\) 的值恰为 \(rank\),则 \(u\) 的 \(key\) 值即为答案;
- 若 \(u\) 的左子树大小 \(+1\) 的值大于 \(rank\),说明答案在左子树里,跳到 \(u\) 的左儿子上;
- 否则答案在右子树里,将 \(rank\) 减去左子树大小再减去 \(u\) 节点,继续跳到 \(u\) 的右儿子上。
写成代码为:
int qkey(int rank)//查询排名 rank 数值
{
int u = root;
while(1)
{
if(tr[tr[u].l].siz + 1 == rank) break;
if(tr[tr[u].l].siz + 1 > rank) u = tr[u].l;
else rank -= tr[tr[u].l].siz + 1, u = tr[u].r;
}
return tr[u].key;
}
给定数 \(key\),如何查找它的前驱与后继呢?
以前驱为例,我们先将原树分裂为 \(<key\)(即 \(\le key-1\))和 \(\ge key\) 两部分,按照有旋 Treap 的经验,不难想到在分裂后左边这一块的根节点上一直跳它的右儿子,最后的那个一定是答案。最后还要合并回去。查询后继同理:
int qpre(int key)//前驱
{
split(root, key - 1, x, y);//分裂
int u = x;
while(tr[u].r) u = tr[u].r;//一直跳右儿子
int res = tr[u].key;
root = merge(x, y);//合并回去
return res;
}
int qnxt(int key)//后继
{
split(root, key, x, y);//分裂
int u = y;
while(tr[u].l) u = tr[u].l;//一直跳左儿子
int res = tr[u].key;
root = merge(x, y);//合并回去
return res;
}
模板题 1 参考代码
其实上面讲的就是模板题 1 里要我们完成的所有操作了,因此来看看总代码:
#include<bits/stdc++.h>
using namespace std;
const int N = 1e5 + 10;
int n;
struct FHQTreap
{
struct Tree
{
int l, r;//左右儿子
int key;//BST 权值
int val;//heap 权值
int siz;//子树大小
}tr[N];
int root;//根节点
int idx;//当前已经分配到了第 idx 个节点
int create(int key)//新建 key 值节点
{
tr[++ idx].key = key;
tr[idx].val = rand();
tr[idx].siz = 1;
return idx;
}
void pushup(int u)//上传信息
{
tr[u].siz = tr[tr[u].l].siz + tr[tr[u].r].siz + 1;
}
void split(int u, int k, int &x, int &y)//分裂区间为 [l, k] 和 (k, r],x 和 y 为虚拟节点
{
if(!u)//当前节点为空节点,虚拟节点赋 0 处理
{
x = y = 0;
return;
}
if(tr[u].key <= k)//分裂右子树
{
x = u;
split(tr[u].r, k, tr[u].r, y);
}
else//分裂左子树
{
y = u;
split(tr[u].l, k, x, tr[u].l);
}
pushup(u);
}
int merge(int u, int v)//合并两个以 u 和以 v 为根的树,并返回新树根节点
{
if(!u) return v;
if(!v) return u;
if(tr[u].val > tr[v].val)//u 为根
{
tr[u].r = merge(tr[u].r, v);//继续合并
pushup(u);
return u;//返回根
}
else//v 为根
{
tr[v].l = merge(u, tr[v].l);//继续合并
pushup(v);
return v;//返回根
}
}
void insert(int key)
{
int x, y;
split(root, key, x, y);
root = merge(merge(x, create(key)), y);
}
void remove(int key)
{
int x, y, z;
split(root, key - 1, x, y);
split(y, key, y, z);
y = merge(tr[y].l, tr[y].r);
root = merge(merge(x, y), z);
}
int qrank(int key)//查询数值 key 排名
{
int x, y;
split(root, key - 1, x, y);
int res = tr[x].siz + 1;
root = merge(x, y);
return res;
}
int qkey(int rank)//查询排名 rank 数值
{
int u = root;
while(1)
{
if(tr[tr[u].l].siz + 1 == rank) break;
if(tr[tr[u].l].siz + 1 > rank) u = tr[u].l;
else rank -= tr[tr[u].l].siz + 1, u = tr[u].r;
}
return tr[u].key;
}
int qpre(int key)//前驱
{
int x, y;
split(root, key - 1, x, y);//分裂
int u = x;
while(tr[u].r) u = tr[u].r;//一直跳右儿子
int res = tr[u].key;
root = merge(x, y);//合并回去
return res;
}
int qnxt(int key)//后继
{
int x, y;
split(root, key, x, y);//分裂
int u = y;
while(tr[u].l) u = tr[u].l;//一直跳左儿子
int res = tr[u].key;
root = merge(x, y);//合并回去
return res;
}
}T;
int main()
{
cin >> n;
while(n --)
{
int op, num;
scanf("%d%d", &op, &num);
if(op == 1) T.insert(num);
else if(op == 2) T.remove(num);
else if(op == 3) printf("%d\n", T.qrank(num));
else if(op == 4) printf("%d\n", T.qkey(num));
else if(op == 5) printf("%d\n", T.qpre(num));
else printf("%d\n", T.qnxt(num));
}
return 0;
}
FHQ-Treap 维护区间操作
以模板题 P3391 【模板】文艺平衡树 为例。
该模板题让我们实现区间反转操作,考虑如何做。
当反转后,所有元素的大小关系颠倒,那么原本大于根节点的都变为了小于根节点的,原本小于根节点的都变为了大于根节点的。所以我们对于区间反转操作,只要将该区间内的元素分裂出来,然后将其左右儿子颠倒,同时递归下去即可。
考虑打懒标记,显然交换两次后相当于没交换,所以可以用异或维护懒标记。懒标记下放时只需交换左右儿子即可。
这是懒标记代码:
void pushdown(int u)
{
if(tr[u].lazy)
{
//用异或处理懒标记
swap(tr[u].l, tr[u].r);
tr[tr[u].l].lazy ^= tr[u].lazy;
tr[tr[u].r].lazy ^= tr[u].lazy;
tr[u].lazy = 0;
}
}
总代码长这样:
#include<bits/stdc++.h>
using namespace std;
const int N = 1e5 + 10;
struct FHQTreap
{
struct Tree
{
int l, r;//左右儿子
int key;//BST 权值
int val;//heap 权值
int siz;//子树大小
bool lazy;//区间反转特用懒标记
}tr[N];
int root;//根节点
int idx;//当前已经分配到了第 idx 个节点
void pushup(int u)//上传信息,类似线段树
{
tr[u].siz = tr[tr[u].l].siz + tr[tr[u].r].siz + 1;
}
void pushdown(int u)
{
if(tr[u].lazy)
{
//用异或处理懒标记
swap(tr[u].l, tr[u].r);
tr[tr[u].l].lazy ^= tr[u].lazy;
tr[tr[u].r].lazy ^= tr[u].lazy;
tr[u].lazy = 0;
}
}
int create(int key)//新建 BST 权值为 key 的节点
{
tr[++ idx].key = key;
tr[idx].val = rand();
tr[idx].siz = 1;
return idx;
}
void split(int u, int k, int &x, int &y)//分裂区间为 [l, k] 和 (k, r],x 和 y 为虚拟节点
{
if(!u)//当前节点为空节点,虚拟节点赋 0 处理
{
x = y = 0;
return;
}
pushdown(u);
if(tr[tr[u].l].siz + 1 <= k)
{
x = u;
split(tr[u].r, k - tr[tr[u].l].siz - 1, tr[u].r, y);
}
else
{
y = u;
split(tr[u].l, k, x, tr[u].l);
}
pushup(u);
}
int merge(int u, int v)
{
if(!u) return v;
if(!v) return u;
pushdown(u), pushdown(v);
if(tr[u].val > tr[v].val)//u 为根
{
tr[u].r = merge(tr[u].r, v);//继续合并
pushup(u);
return u;//返回根
}
else//v 为根
{
tr[v].l = merge(u, tr[v].l);//继续合并
pushup(v);
return v;//返回根
}
}
}T;
int n, m;
int l, r;
int lr, rr, mr;
void dfs(int u)//遍历,输出答案
{
if(!u) return;
if(T.tr[u].lazy)
{
swap(T.tr[u].l, T.tr[u].r);
T.tr[T.tr[u].l].lazy = !T.tr[T.tr[u].l].lazy;
T.tr[T.tr[u].r].lazy = !T.tr[T.tr[u].r].lazy;
T.tr[u].lazy = 0;
}
dfs(T.tr[u].l);
printf("%d ", T.tr[u].key);
dfs(T.tr[u].r);
}
int main()
{
cin >> n >> m;
for(int i = 1; i <= n; i ++)//原始序列
{
T.create(i);
T.root = T.merge(T.root, T.idx);
}
while(m --)
{
scanf("%d%d", &l, &r);
T.split(T.root, r, lr, rr);
T.split(lr, l - 1, lr, mr);
T.tr[mr].lazy = !T.tr[mr].lazy;
T.root = T.merge(T.merge(lr, mr), rr);
}
dfs(T.root);
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号