【线段树合并】学习笔记

前置知识：线段树、动态开点、权值线段树。

---

我们现在假设有如图所示两棵线段树（省略区间信息）：

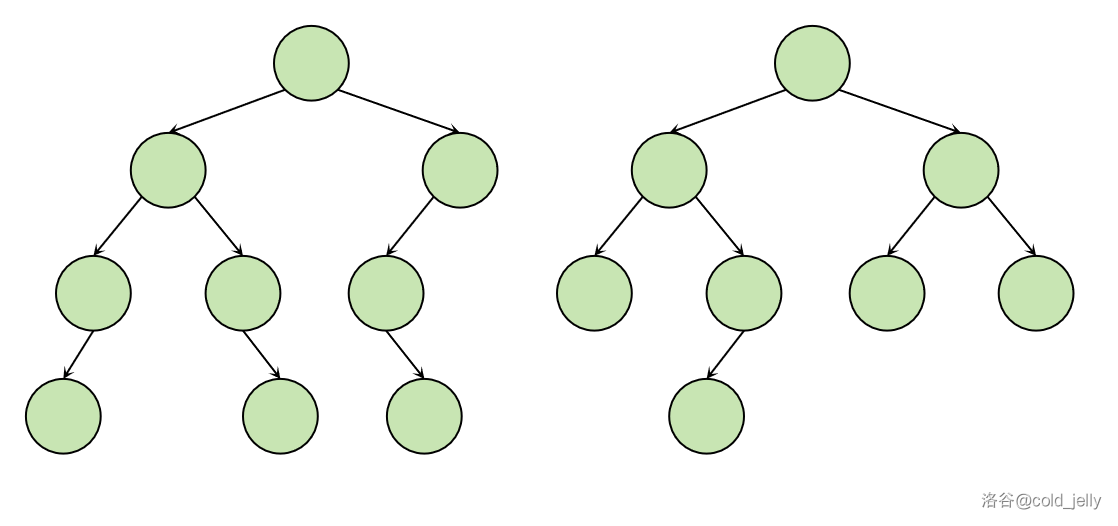
合并（merge）操作就是将这两棵线段树按某种方式组合成一棵新线段树，并且所有节点权值的组合方式应一致。

首先，我们要清楚，线段树合并本质上是一个相当暴力的过程，我们直接在两棵线段树上跑 DFS，对当前节点左右儿子情况进行分类讨论，再合并节点信息（例如求和、取 \(\max\) 等）即可。如果不考虑记录合并前线段树的信息的话，我们可以直接将新的信息覆盖在其中一棵线段树上，本文以覆盖在第二棵线段树上为例。

我们根据图示看看上图两棵线段树如何合并（黄色节点表示已遍历）。

前几个遍历到的节点中，节点左右儿子情况一致，直接将信息合并：

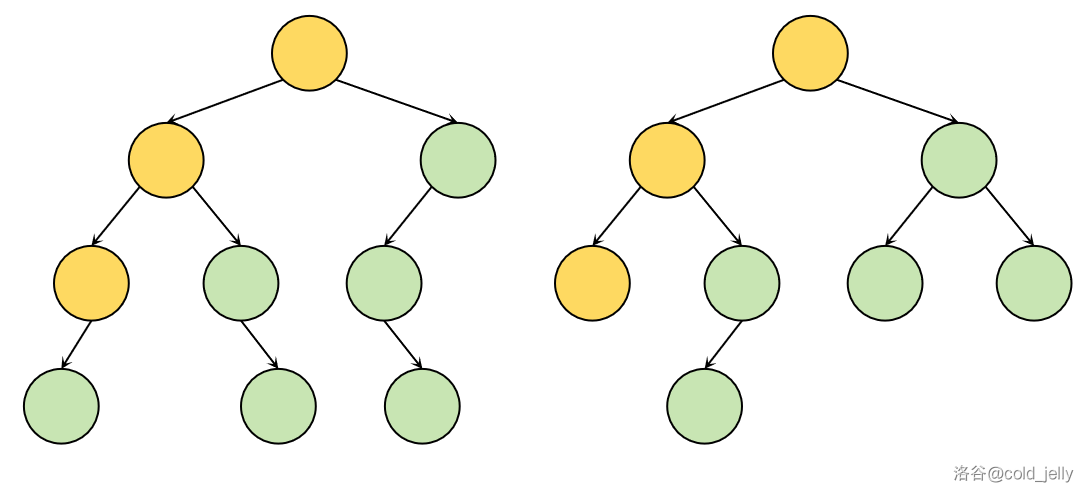
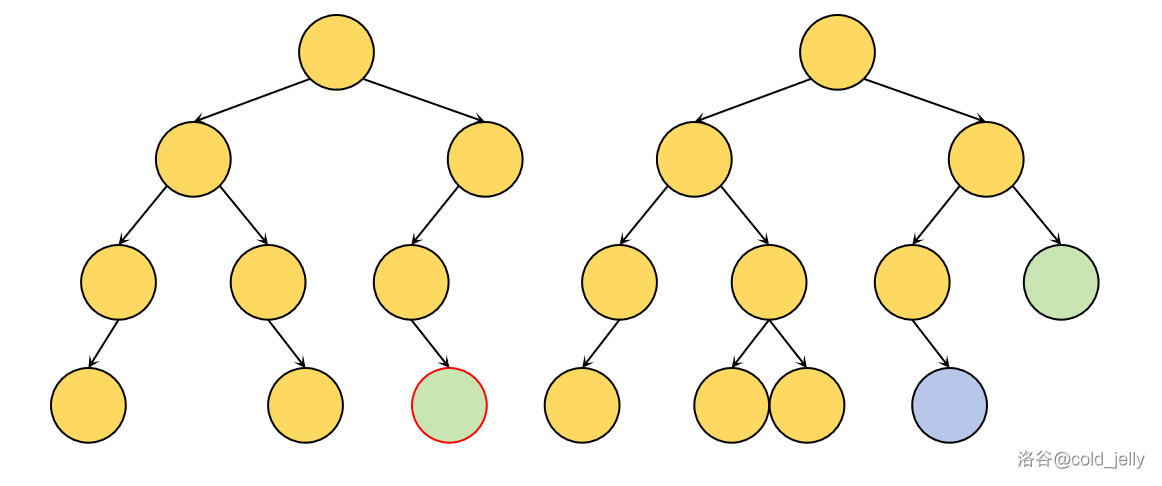
遍历到了图中红边节点（左边的线段树）时，我们发现右边线段树上对应节点没有左儿子，我们可以直接开一个新点（蓝色节点），该新点储存的信息与红边节点左儿子的信息一致，并将其连在右边线段树上：

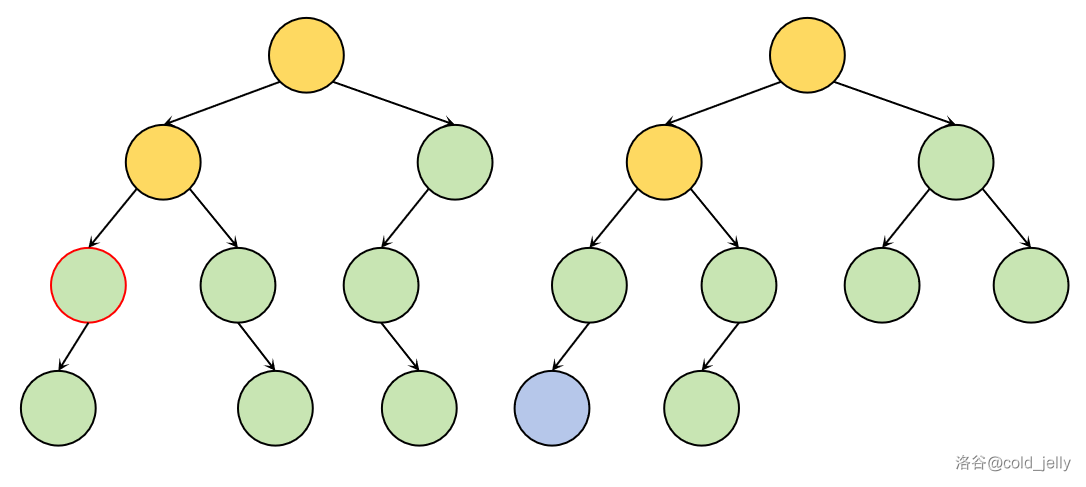
继续接着遍历至下图中红边节点，此时与右边线段树上对应节点左右儿子情况比较。因为我们要将信息覆盖到右边线段树上，所以可以不用管左边线段树的空左儿子，只用考虑将其右儿子直接搬到右边即可，方法与上面的一致：

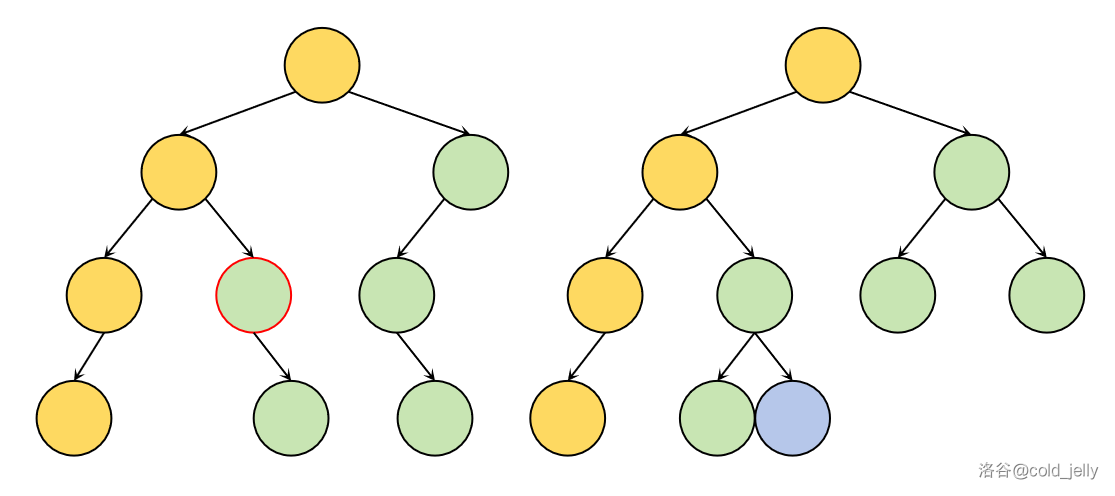
依次类推：

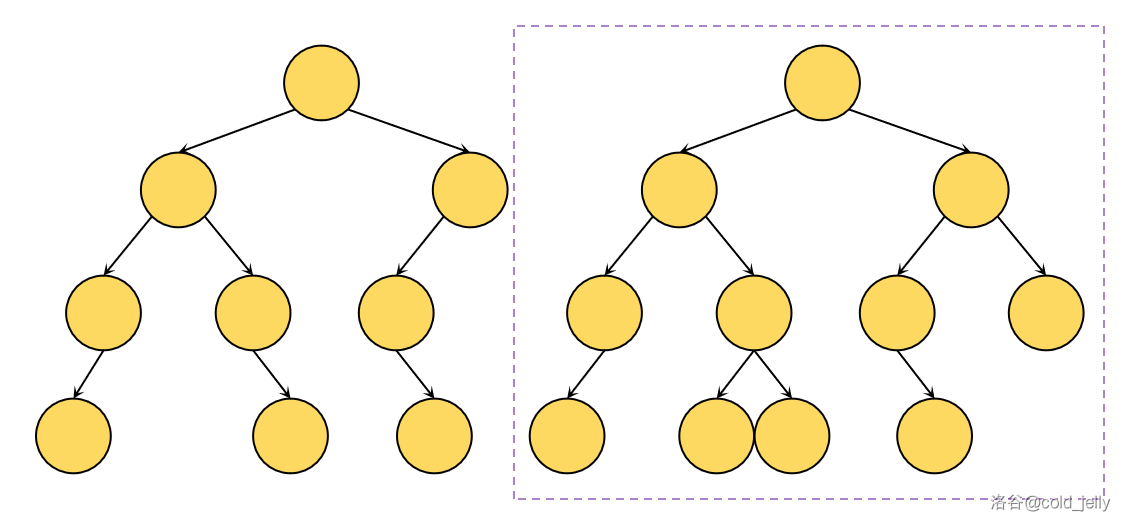
此时右边用紫色矩形框起来的就是合并后的线段树了。

由此我们可以总结出合并时的具体操作情况：

• 若两树对应节点有一边为空，就直接把一边信息直接复制到另一边；
• 否则就直接合并信息即可。

对应地可以写出代码：

int merge(int u, int v, int l, int r)//线段树合并 
{
	if(!u) return v;//空儿子 
	if(!v) return u;//同上 
	if(l == r)
	{
//		这里是具体的信息合并处理操作 
		return u;
	}
	int mid = (l + r) / 2;
	tr[u].l = merge(tr[u].l, tr[v].l, l, mid);//继续遍历 
	tr[u].r = merge(tr[u].r, tr[v].r, mid + 1, r);//继续遍历 
	pushup(u);//上传信息 
	return u;
}