【李超线段树】学习笔记
前置知识:线段树、基础解析几何知识。
本篇文章参考了 Glacial_Shine 的这篇文章,在此一并感谢。
简介
李超线段树是一种用于维护平面直角坐标系内线段关系的数据结构。
具体而言,李超线段树支持在平面直角坐标系中动态插入线段,支持快速询问给定竖线与所有线段交点的最大纵坐标。
例如,例题 P4097 【模板】李超线段树 / [HEOI2013] Segment 中,需要我们完成的操作:
- 在平面直角坐标系中插入一条线段;
- 给定 \(k\),求所有线段与直线 \(x=k\) 的交点的纵坐标最大值。
就可以用李超线段树维护。
如果还不理解的话,下图展示了插入了 \(5\) 条线段后,分别询问 \(k=3,6\) 的答案点:
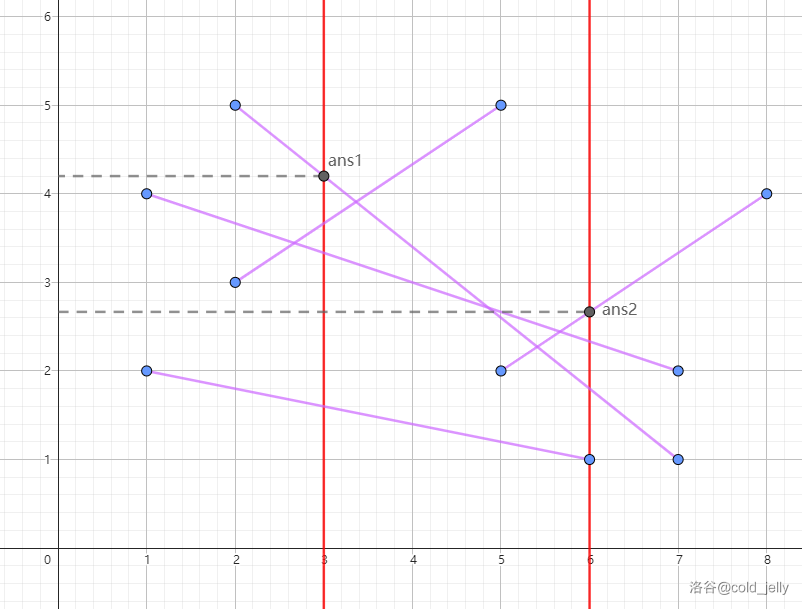
原理与实现
李超线段树是线段树的一种,所以其操作与普通线段树的操作基本一致。
以上面的例题为例,我们来好好讲讲李超线段树的原理。
对于一个研究区间,我们只关心该区间中的最优线段。何为最优线段?我们规定在区间 \([L,R]\) 中,与直线 \(x=\dfrac{L+R}{2}\) 交点纵坐标最大的线段为该区间内的最优线段。李超线段树通过维护小区间内的最优线段,然后在每次询问某节点的最优线段时遍历这个节点到根节点的路径,从路径中的所有最优线段中找出答案。
对于例题中的第一种操作,即插入操作(insert),我们不妨考虑即将插入的这条线段对一定区间内维护的最优线段的影响情况。
采用分类讨论的思想,我们不难发现可以分为这样几种情况:
- 该线段与区间没有交集,因此对区间内维护的最优线段没有影响;
- 该线段与区间有交集,但区间不是该线段定义域的子集,此时考虑递归到该区间的左右子区间作进一步细化处理;
- 区间是该线段定义域的子集,此时分三种情况讨论:
- 若该线段在区间两端点处纵坐标均比该区间内原先最优线段的大,那么可以形象地理解为该线段在该区间内完全碾压原先最优线段,往后该区间内其不可能再成为最优线段了,所以该线段成为新的最优线段,原本的舍弃;
- 若该线段在区间两端点处纵坐标均比该区间内原先最优线段的小,那么可以形象地理解为该线段在该区间内被原先最优线段完全碾压,同上,区间内最优线段不做任何修改,将该线段舍弃;
- 否则,该线段与原先的最优线段一定有交点,考虑最优线段的定义,我们比较在区间中点 \(mid=\dfrac{L+R}{2}\) 处两条线段对应的纵坐标谁大,将大的那条作为新的最优线段。但由于这两条线段相互之间都不能被对方完全碾压,所以考虑将没成为最优线段的那条线段往该区间的左右子区间下放,作递归处理(只需要往有比最优线段更优的一端递归即可)。
可以结合下面的图示理解(黑色线段为待插入线段,蓝色线段为区间原先最优线段):
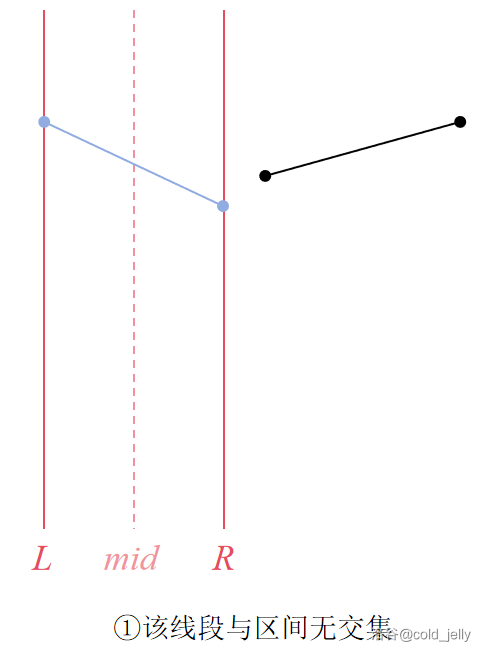
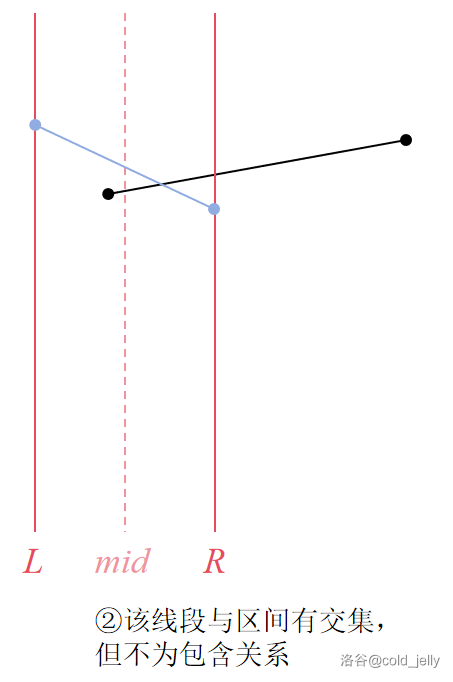
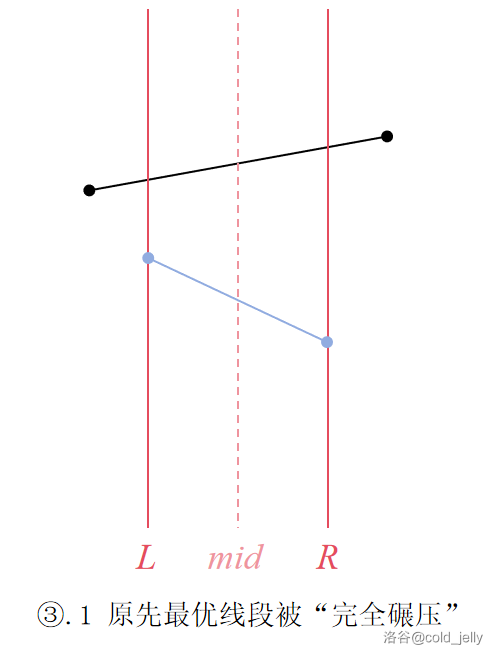
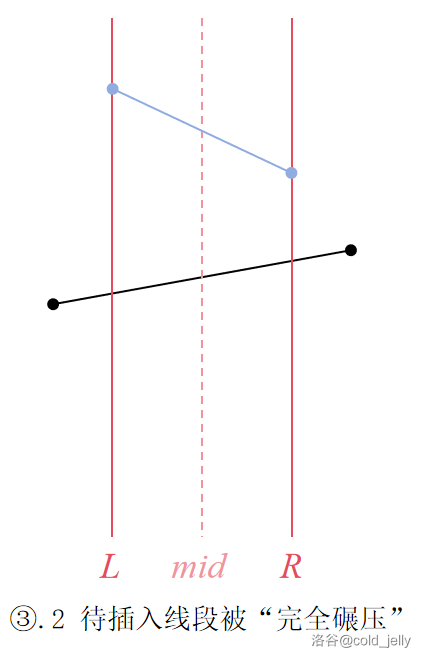
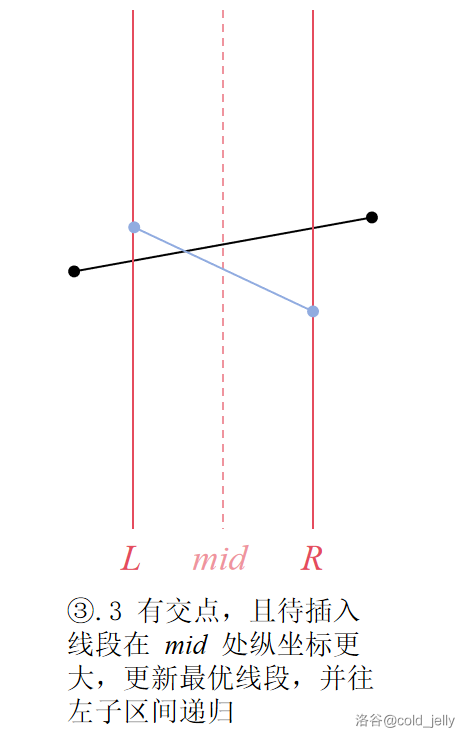
李超线段树需要好好根据示意图来理解,如果没懂的话再反复看几遍。
具体实现的话可以参考代码:
inline double Ycalc(int i, int X)//计算纵坐标
{
return line[i].k * X + line[i].b;
}
inline bool cmp(int i, int j, int X)//比较编号为 i 和 j 的线段在 X 处的纵坐标
{
//由于精度误差,不能直接比较
if(Ycalc(i, X) - Ycalc(j, X) > eps) return true;
if(Ycalc(j, X) - Ycalc(i, X) > eps) return false;
return i < j;
}
void insert(int &u, int l, int r, int L, int R, int id)//插入线段,编号为 id
{
//区间为 [l, r]
if(r < L || R < l) return;//线段与该区间不交
if(!u) u = ++ cnt;//动态开点
if(L <= l && r <= R)//线段完全覆盖该区间
{
if(cmp(id, tr[u].id, l) && cmp(id, tr[u].id, r))//该线段比当前区间最优线段完全更优
{
tr[u].id = id;
return;
}
if(cmp(tr[u].id, id, l) && cmp(tr[u].id, id, r))//该线段比当前区间最优线段完全更劣
return;
//两线段有交点,都不能完全覆盖彼此
int mid = (l + r) / 2;
if(cmp(id, tr[u].id, mid)) swap(id, tr[u].id);
//处理左右子区间
if(cmp(id, tr[u].id, l)) insert(tr[u].l, l, mid, L, R, id);
if(cmp(id, tr[u].id, r)) insert(tr[u].r, mid + 1, r, L, R, id);
}
else//线段覆盖部分该区间
{
int mid = (l + r) / 2;
//处理左右子区间
insert(tr[u].l, l, mid, L, R, id);
insert(tr[u].r, mid + 1, r, L, R, id);
}
}
我的李超线段树是用动态开点实现的,所以不需要建树。
线段在树上被分割为 \(\log n\) 个小区间,最多向下递归 \(\log n\) 层,因此插入操作的时间复杂度是 \(O(\log^2 n)\) 的。
对于例题中的第二种操作,即查询操作(query),我们在树上查询,在路径上的所有区间的最优线段找到最优的那一个,注意本题所求的是线段的编号 \(id\)。
void query(int u, int l, int r, int X)
{
if(!u || r < X || X < l) return;
if(cmp(tr[u].id, ans, X)) ans = tr[u].id;//比较路径上的最优线段,记录编号
if(l == r) return;
//在树上往下查询最优线段
int mid = (l + r) / 2;
query(tr[u].l, l, mid, X);
query(tr[u].r, mid + 1, r, X);
}
同插入操作的分析,查询操作的时间复杂度是 \(O(\log n)\) 的。
分析完毕,建议反复看几遍加深理解,实在不行可以再结合总代码理解:
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N = 1e5 + 10;
const double eps = 1e-10;//调精度
struct Line//线段
{
double k, b;//直线参数
}line[N];
int n, op, k, x_0, x_1, y_0, y_1;
const int mod1 = 39989, mod2 = 1e9;
int ans, lastans;
int root;
int Lcnt;
struct LiChaoSegmentTree//李超线段树
{
int cnt;
struct Tree
{
int l, r;//区间左右端点
int id;//编号
}tr[N * 4];
inline double Ycalc(int i, int X)//计算纵坐标
{
return line[i].k * X + line[i].b;
}
inline bool cmp(int i, int j, int X)//比较编号为 i 和 j 的线段在 X 处的纵坐标
{
//由于精度误差,不能直接比较
if(Ycalc(i, X) - Ycalc(j, X) > eps) return true;
if(Ycalc(j, X) - Ycalc(i, X) > eps) return false;
return i < j;
}
void insert(int &u, int l, int r, int L, int R, int id)//插入线段,编号为 id
{
//区间为 [l, r]
if(r < L || R < l) return;//线段与该区间不交
if(!u) u = ++ cnt;//动态开点
if(L <= l && r <= R)//线段完全覆盖该区间
{
if(cmp(id, tr[u].id, l) && cmp(id, tr[u].id, r))//该线段比当前区间最优线段完全更优
{
tr[u].id = id;
return;
}
if(cmp(tr[u].id, id, l) && cmp(tr[u].id, id, r))//该线段比当前区间最优线段完全更劣
return;
//两线段有交点,都不能完全覆盖彼此
int mid = (l + r) / 2;
if(cmp(id, tr[u].id, mid)) swap(id, tr[u].id);
//处理左右子区间
if(cmp(id, tr[u].id, l)) insert(tr[u].l, l, mid, L, R, id);
if(cmp(id, tr[u].id, r)) insert(tr[u].r, mid + 1, r, L, R, id);
}
else//线段覆盖部分该区间
{
int mid = (l + r) / 2;
//处理左右子区间
insert(tr[u].l, l, mid, L, R, id);
insert(tr[u].r, mid + 1, r, L, R, id);
}
}
void query(int u, int l, int r, int X)
{
if(!u || r < X || X < l) return;
if(cmp(tr[u].id, ans, X)) ans = tr[u].id;//比较路径上的最优线段,记录编号
if(l == r) return;
//在树上往下查询最优线段
int mid = (l + r) / 2;
query(tr[u].l, l, mid, X);
query(tr[u].r, mid + 1, r, X);
}
}T;
signed main()
{
cin >> n;
for(int i = 1; i <= n; i ++)
{
scanf("%lld", &op);
if(op == 0)
{
scanf("%lld", &k);
k = (k + lastans - 1) % mod1 + 1;
ans = 0;
T.query(1, 1, mod1, k);
printf("%lld\n", ans);
lastans = ans;
}
else
{
scanf("%lld%lld%lld%lld", &x_0, &y_0, &x_1, &y_1);
x_0 = (x_0 + lastans - 1) % mod1 + 1;
x_1 = (x_1 + lastans - 1) % mod1 + 1;
y_0 = (y_0 + lastans - 1) % mod2 + 1;
y_1 = (y_1 + lastans - 1) % mod2 + 1;
if(x_1 < x_0)
{
swap(x_1, x_0);
swap(y_1, y_0);
}
Lcnt ++;
if(x_1 != x_0)
{
line[Lcnt].k = 1.0 * (y_1 - y_0) / (x_1 - x_0);
line[Lcnt].b = 1.0 * y_0 - line[Lcnt].k * x_0;
}
else//特殊处理竖直线段
{
line[Lcnt].k = 0;
line[Lcnt].b = max(y_0, y_1);
}
T.insert(root, 1, mod1, x_0, x_1, Lcnt);
}
}
return 0;
}
个人感觉马蜂海星,将就着看吧= ̄ω ̄=。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号