【树链剖分】学习笔记

板子：P3384 【模板】重链剖分/树链剖分

建议先阅读完题面，了解几个操作后再看文章。

树链剖分的核心思想就是把树剖分成若干条链，从而将树上问题转化为序列问题，便于我们使用数据结构来维护信息、优化算法。

常见的树链剖分有重链剖分、长链剖分等，本文主要介绍重链剖分。

本文的符号表示与基本定义：

\(siz[u]\)：树上以节点 \(u\) 为根的子树大小；
\(dep[u]\)：节点 \(u\) 的深度；
\(fa[u]\)：节点 \(u\) 的父节点编号；
\(root\)：根节点编号；
\(w[u]\)：初始点权。

重链剖分

为实现重链剖分，我们规定：

重子节点（heavy son）：树上一个节点 \(u\) 的所有子节点中子树大小最大的称为该节点的重子节点，用符号表示为 \(hs[u]\)，如果有多个，取其一；
轻子节点（soft son）：树上一个节点 \(u\) 的所有子节点中除其重子节点的均叫做该节点的轻子节点；
重边与轻边：父节点与其重子节点的连边叫做重边，与其轻子节点的连边叫做轻边；
重链：相邻重边连起来的连接一条重子节点的链叫重链，特别地，对于轻叶子节点，其属于一条以自己为起点的长度为 \(1\) 的重链。

例如，下图中粉色节点为所有重子节点，浅蓝色节点为所有轻子节点，粉色边为重边，黑色边为轻边，节点旁边的紫色数字为 \(siz[u]\)。

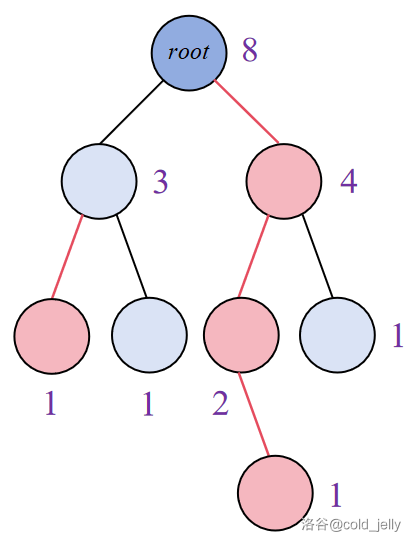
那么根据重链的定义，该图中所有的重链如图所示：

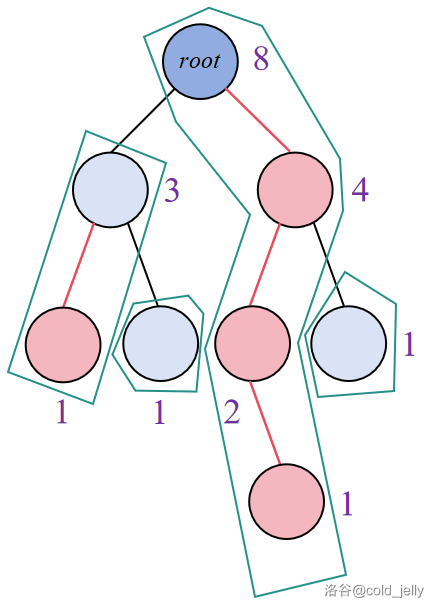
把一棵树剖分成若干条重链的过程就是重链剖分。

注意到，重链剖分后，每个节点均属于一条重链，我们把节点 \(u\) 所在重链中深度最小的节点叫做该重链的链顶，记作 \(top[u]\)。

重链剖分的过程

重链剖分总体实现分为两个 DFS。

第一个 DFS 需要预处理 \(dep[u]\)、\(fa[u]\)、\(siz[u]\)、\(hs[u]\)，具体实现可见代码（还是比较好理解的）：

void dfs1(int u, int father)
{
	dep[u] = dep[father] + 1;
	fa[u] = father;
	siz[u] = 1;
	int maxson = -1;//记录 u 的重子节点的儿子数 
	for(auto i : e[u])
	{
		if(i == father) continue;
		dfs1(i, u);
		siz[u] += siz[i];
		if(siz[i] > maxson)//记录重子节点 
		{
			hs[u] = i;
			maxson = siz[i];
		}
	}
}

第二个 DFS 需要预处理的有：

每个点在剖分后的新编号 \(id[u]\)；
赋值每个点的点权到新编号上点权 \(wt[u]\)；
链顶 \(top[u]\)；
处理每条链。

具体实现参考代码：

void dfs2(int u, int topf)
{
	id[u] = ++ cnt;//标记 u 节点新编号 
	wt[cnt] = w[u];//赋值点权到新编号上 
	top[u] = topf;//处理链顶 
	if(hs[u] == 0) return;//没有子节点 
	dfs2(hs[u], topf);//先处理重子节点 
	for(auto i : e[u])//后处理轻子节点 
	{
		if(i == fa[u] || i == hs[u]) continue;
		dfs2(i, i);
		//每个轻子节点都有一条以它为链顶的重链 
	}
}

为什么我们要先处理重子节点，后处理轻子节点呢？这是因为如果我们这样做的话，每条重链的节点编号都是连续的，便于我们后续序列处理。

例如对于上面的树，处理后各节点新编号 \(id[u]\) 如图所示：

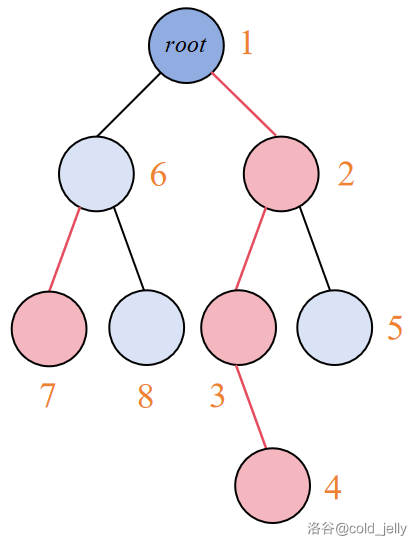
并且由于 DFS，每个子树的节点编号也是连续的。

解决问题

对于树上两点之间路径的操作，我们可以在每条重链上操作，具体而言：

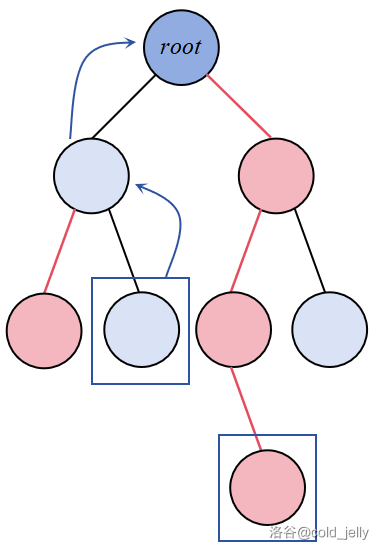
假设我们要处理的点为图中两个被深蓝色方形框住的节点，那么我们可以这样做：

比较两节点深度，取所在重链的链顶的深度更大的为操作点（记作 \(x\)）；
对于 \(x\) 所在重链，由于其编号连续，所以可以用线段树处理区间问题（区间修改与区间求和）；
处理完该重链后，操作点跳至 \(fa[top[x]]\)，即令 \(x=fa[top[x]]\)；
重复执行 2~3 步，直到 \(x\) 跳到另一待处理点所在重链上时，处理该重链上的区间问题。

树上跳点的复杂度为 \(O(\log n)\)，线段树区间操作复杂度为 \(O(\log n)\)，所以单次树上路径操作的复杂度是 \(O(\log^2 n)\) 的。

单点修改与单点查询就更简单了，直接在线段树上操作即可，复杂度为 \(O(\log n)\)。

附模板题代码：

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N = 1e5 + 10;
int n, m, root, mod;
int op, x, y, z;
vector<int> e[N];
int w[N];//初始点权 
int dep[N];//deep 节点深度 
int fa[N];//father 节点的父亲编号 
int siz[N];//size 子树大小 
int hs[N];//heavy son 节点的重子节点编号 
int id[N], cnt;//每个节点的新编号 
int wt[N];//赋值新编号点权 
int top[N];//当前节点所在重链的链顶 
struct SegmentTree//线段树 
{
	struct Tree
	{
		int l, r;
		int sum, add;
	}tr[N * 4];
	void pushup(int u)
	{
		tr[u].sum = tr[u * 2].sum + tr[u * 2 + 1].sum + mod;
		tr[u].sum %= mod;
	}
	void pushdown(int u)
	{
		auto &root = tr[u];
		auto &lson = tr[u * 2];
		auto &rson = tr[u * 2 + 1];
		if(root.add)
		{
			lson.add += root.add;
			lson.add %= mod;
			lson.sum += (lson.r - lson.l + 1) * root.add + mod;
			lson.sum %= mod;
			rson.add += root.add;
			rson.add %= mod;
			rson.sum += (rson.r - rson.l + 1) * root.add + mod;
			rson.sum %= mod;
			root.add = 0;
		}
	}
	void build(int u, int l, int r)
	{
		if(l == r)
		{
			tr[u] = {l, r, wt[r] % mod, 0};
			return;
		}
		tr[u] = {l, r, 0, 0};
		int mid = (l + r) / 2;
		build(u * 2, l, mid);
		build(u * 2 + 1, mid + 1, r);
		pushup(u);
	}
	void modify(int u, int l, int r, int k)
	{
		if(tr[u].l >= l && tr[u].r <= r)
		{
			tr[u].sum += (tr[u].r - tr[u].l + 1) * k + mod;
			tr[u].sum %= mod;
			tr[u].add += k;
			tr[u].add %= mod;
			return;
		}
		pushdown(u);
		int mid = (tr[u].l + tr[u].r) / 2;
		if(l <= mid) modify(u * 2, l, r, k);
		if(r > mid) modify(u * 2 + 1, l, r, k);
		pushup(u);
	}
	int query(int u, int l, int r)
	{
		if(tr[u].l >= l && tr[u].r <= r)
			return tr[u].sum;
		pushdown(u);
		int mid = (tr[u].l + tr[u].r) / 2;
		int res = 0;
		if(l <= mid) (res += query(u * 2, l, r)) %= mod;
		if(r > mid) (res += query(u * 2 + 1, l, r)) %= mod;
		return res;
	}
}T;
void Rmodify(int x, int y, int z)//路径修改 
{
	while(top[x] != top[y])//往上跳 
	{
		if(dep[top[x]] < dep[top[y]]) swap(x, y);
		T.modify(1, id[top[x]], id[x], z);
		x = fa[top[x]];//跳到上一条重链 
	}
	if(id[x] > id[y]) swap(x, y);
//	or dep[x] > dep[y]
	T.modify(1, id[x], id[y], z);
}
int Rquery(int x, int y)//路径查询 
{
	int res = 0;
	while(top[x] != top[y])//往上跳 
	{
		if(dep[top[x]] < dep[top[y]]) swap(x, y);
		res += T.query(1, id[top[x]], id[x]);
		res %= mod;
		x = fa[top[x]];//跳到上一条重链 
	}
	if(id[x] > id[y]) swap(x, y);
//	or dep[x] > dep[y]
	res += T.query(1, id[x], id[y]);
	res %= mod;
	return res;
}
void dfs1(int u, int father)
{
	dep[u] = dep[father] + 1;
	fa[u] = father;
	siz[u] = 1;
	int maxson = -1;//记录 u 的重子节点的儿子数 
	for(auto i : e[u])
	{
		if(i == father) continue;
		dfs1(i, u);
		siz[u] += siz[i];
		if(siz[i] > maxson)//记录重子节点 
		{
			hs[u] = i;
			maxson = siz[i];
		}
	}
}
void dfs2(int u, int topf)
{
	id[u] = ++ cnt;//标记 u 节点新编号 
	wt[cnt] = w[u];//赋值点权到新编号上 
	top[u] = topf;//处理链顶 
	if(hs[u] == 0) return;//没有子节点 
	dfs2(hs[u], topf);//先处理重子节点 
	for(auto i : e[u])//后处理轻子节点 
	{
		if(i == fa[u] || i == hs[u]) continue;
		dfs2(i, i);
		//每个轻子节点都有一条以它为链顶的重链 
	}
}
/*
因为先处理重子节点，后处理轻子节点 
所以每条重链的新编号是连续的
因为 DFS，所以每个子树的新编号也是连续的 
*/
signed main()
{
	cin >> n >> m >> root >> mod;
	for(int i = 1; i <= n; i ++) scanf("%lld", &w[i]);
	for(int i = 1; i < n; i ++)
	{
		scanf("%lld%lld", &x, &y);
		e[x].push_back(y);
		e[y].push_back(x);
	}
	dfs1(root, 0);
	dfs2(root, root);
	T.build(1, 1, n);
	while(m --)
	{
		scanf("%lld", &op);
		if(op == 1)
		{
			scanf("%lld%lld%lld", &x, &y, &z);
			Rmodify(x, y, z);
		}
		else if(op == 2)
		{
			scanf("%lld%lld", &x, &y);
			printf("%lld\n", Rquery(x, y));
		}
		else if(op == 3)
		{
			scanf("%lld%lld", &x, &z);
			T.modify(1, id[x], id[x] + siz[x] - 1, z);
		}
		else
		{
			scanf("%lld", &x);
			printf("%lld\n", T.query(1, id[x], id[x] + siz[x] - 1));
		}
	}
	return 0;
}

树链剖分求 LCA

大致过程与树剖做树上路径操作一样，都是在重链上跳，时间复杂度为 \(O(\log n)\)。

int LCA(int x, int y)
{
	while(top[x] != top[y])
	{
		if(dep[top[x]] < dep[top[y]]) swap(x, y);
		x = fa[top[x]];
	}
	if(dep[x] < dep[y]) return x;
	else return y;
}

代码实现也比倍增求 LCA 简单一些。

posted @ 2025-05-20 14:31 cold_jelly 阅读(64) 评论(0) 收藏举报

刷新页面返回顶部

cold_jelly 的小窝

【树链剖分】学习笔记

重链剖分

重链剖分的过程

解决问题

树链剖分求 LCA

公告