【对拍】学习笔记
前几天听 zrf 讲了对拍,深知其重要性,特此写一篇笔记来巩固(维护看百合看傻的脑袋)。
相较于调试,对拍查错效果更好,因此在正式比赛中使用对拍可以降低挂分概率,是一种十分值得学习的技巧。
一般来说,在正式比赛时,对于我们会的一道题,为减少容错,我们会写两份代码:一份时间复杂度正确但不保证正确性的“正解”以及一份暴力但保证正确性的代码。为检验“正解”的正确性,我们会把“正解”与暴力程序对拍。
以一个简单的例子来解释对拍:
区间求和问题:给定长度为 \(n\) 的序列 \(\{a_n\}\),并给定 \(Q\) 次询问,每次询问给出 \((l_i,r_i)\),求 \(\displaystyle \sum^{r_i}_{k=l_i}a_k\)。(\(1\le n,Q\le 10^5\),\(1\le a_i\le 10^9\))
相信每个 OIer 都会做这题的正解(例如前缀和、树状数组、线段树等等),这里以前缀和方法为例,演示该题的“正解”:
#include<bits/stdc++.h>
using namespace std;
const int N = 1e5 + 10;
int n, Q;
int a[N], pre[N];
int main()
{
cin >> n >> Q;
for(int i = 1; i <= n; i ++)
{
scanf("%d", &a[i]);
pre[i] = pre[i - 1] + a[i];
}
while(Q --)
{
int l, r;
scanf("%d%d", &l, &r);
printf("%d\n", pre[r] - pre[l - 1]);
}
return 0;
}
以上是复杂度为 \(O(n+Q)\) 的前缀和做法(本地文件名为 std.cpp)。但该代码存在问题,因为在本题 \(1\le a_i\le 10^9\) 的数据范围下会爆 int。但是由于一些神秘的原因(磕百合?),我们并没有发现此问题。那咋办呐......>_<。
这时对拍就发挥作用了,我们可以写一个暴力程序(前提要保证自己的暴力没写错):
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N = 1e5 + 10;
int n, Q;
int a[N];
signed main()
{
cin >> n >> Q;
for(int i = 1; i <= n; i ++) scanf("%lld", &a[i]);
while(Q --)
{
int l, r, sum = 0;
scanf("%lld%lld", &l, &r);
for(int i = l; i <= r; i ++) sum += a[i];
printf("%lld\n", sum);
}
return 0;
}
我们在本地保存为 BF.cpp,此时文件夹里面是这样滴:
这时可能就有同学要问了:“难道我们还要自己手搓数据来运行对比吗?”。当然不是啦,这样还要对拍干嘛。我们肯定希望对拍实现全自动,即造数据以及运行、对比都应交由计算机完成啊。
所以我们还需额外写两个辅助程序:数据生成器的 seed.cpp 以及对拍启动器 runer.cpp。
首先来看数据生成器(以 \(n=10\),生成 \(Q=10\) 组 \((l_i,r_i)\) 为例),先把代码贴出来:
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int MAXN = 10, V = 1e9;
signed main()
{
random_device seed;
mt19937 rd(seed());
freopen("test.in", "w", stdout);
int n = 10, Q = 10;
printf("%lld %lld\n", n, Q);
for(int i = 1; i <= 10; i ++)
{
int a = rd() % V + 1;
printf("%lld ", a);
}
puts("");
for(int i = 1; i <= 10; i ++)
{
int l = rd() % MAXN + 1;
int r = rd() % MAXN + 1;
if(l > r) swap(l, r);
printf("%lld %lld\n", l, r);
}
return 0;
}
我们来逐行分析。
代码中 MAXN 与 V 分别代表了 \(n\) 与 \(a_i\) 的最大取值,即上界。我们将产生的随机数对上界取模,即可得到在我们想要的范围内的随机数。
代码中产生随机数的核心部分:
random_device seed;
mt19937 rd(seed());
注意到,我们并没有采用 rand() 函数,原因是 rand() 函数生成的随机数值域为 \([0,32767]\),很小,无法满足我们的需求。即使使用 rand() << 15 + rand() 的方法强行扩张值域,也会使得随机性大大降低。而使用上述代码中的 mt19937 产生的随机数质量更高,且值域为 C++ 中的 unsigned int,故笔者更推荐大家使用这种随机数生成方式。
接下来 freopen("test.in", "w", stdout); 语句在文件夹中生成了 test.in 文件,方便以后的对拍启动器使用:

然后就正常地生成随机数就行了。其中注意,我们在生成 \(l\) 和 \(r\) 时特判了一句,这是编写数据生成器时需要注意的一点,即一定要保证生成的数据合法。
检验一下数据成果:
10 10
412496533 119216747 495923607 931352602 26313294 552602826 745457913 213446827 119067790 188234191
1 3
1 5
1 2
4 9
8 9
5 10
7 7
4 5
8 10
7 8
海星╰( ̄ω ̄o)。
但是这样会有一定问题,由于种子固定,生成的随机数每次都是相同的,所以我们可以将代码改成这样:
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int MAXN = 10, V = 1e9;
int seed;
signed main()
{
freopen("tp.in", "r", stdin);
cin >> seed;
mt19937 rd(seed);
freopen("tp.in", "w", stdout);
cout << rd();
freopen("test.in", "w", stdout);
int n = 10, Q = 10;
printf("%lld %lld\n", n, Q);
for(int i = 1; i <= 10; i ++)
{
int a = rd() % V + 1;
printf("%lld ", a);
}
puts("");
for(int i = 1; i <= 10; i ++)
{
int l = rd() % MAXN + 1;
int r = rd() % MAXN + 1;
if(l > r) swap(l, r);
printf("%lld %lld\n", l, r);
}
return 0;
}
修改后,利用 tp.in 文件,我们将每次给予的种子也作随机化处理,避免了上述问题。
接下来就是对拍启动器 runer.cpp 啦。还是先贴上代码:
#include<bits/stdc++.h>
using namespace std;
int main()
{
while(1)
{
system("seed.exe");
system("BF.exe < test.in > test.ans");
system("std.exe < test.in > test.out");
if(system("fc test.out test.ans")) return 0;
}
return 0;
}
对拍启动器实现了将测试数据分别导入暴力以及“正解”程序中运行,得到两份输出并比较的过程。具体而言:
- 语句
system("seed.exe");运行数据生成器,得到测试点输入文件test.in; - 语句
system("BF.exe < test.in > test.ans");将test.in导入暴力程序运行,并将运行得到的输出存入文件test.ans,此处的<与>代表数据流向,类似于漏斗的作用; - 语句
system("std.exe < test.in > test.out");同上,得到“正解”输出; - 语句
system("fc test.out test.ans")中fc是比较指令,可以实现比较两输出文件test.out和test.ans内容,根据有无差异返回true或false; while(1)则实现了重复执行直到发现差异的功能。
运行 runer.cpp,此时文件夹里长这样:

命令行界面长这样:
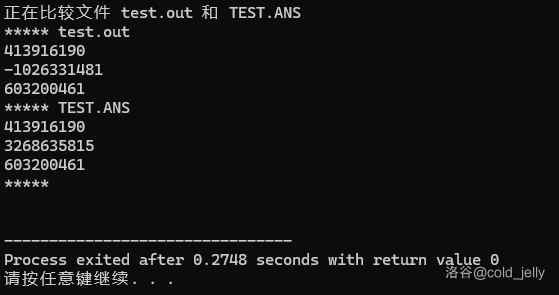
运用聪明的眼睛观察,输出文件的第二行不一样,我们的“正解”居然输出了负数!从这我们就珂以看出是我们的正解爆 int 了。
于是我们成功通过对拍找出了“正解”中的问题,如果在正式考试中,则避免了因该问题而挂分。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号