【斜率优化 DP】学习笔记

前置知识：单调队列优化 DP、基础解析几何知识。

---

斜率优化 DP（以下简称“斜优”）是一种 DP 优化方法。

我们都知道对于 \(O(n^2)\) 的转移：\(dp_i=\min^{j<i}_{j=1}\{dp_j+v_i\}\)。

将其变形为 \(\displaystyle dp_i=\min^{j<i}_{j=1}\{dp_j\}+v_i\) 后可以用单调队列将其优化至 \(O(n)\)。

但是，对于形如 \(\displaystyle dp_i=\min^{j<i}_{j=1}\{dp_j\times v_i+w_i\}\) 的转移的优化问题，由于含有 \(dp_j\times v_i\) 这样既含有 \(i\)、也含有 \(j\) 的项，因此不能使用单调队列来优化，这时就要使用斜优。

以 P3195 [HNOI2008] 玩具装箱 为例来分析斜优原理。

（这不是重点）首先分析得到暴力 \(O(n^2)\) 的转移：\(\displaystyle dp_i=\min^{j<i}_{j=1}\{dp_j+\left(pre_i+i-pre_j-j-L-1\right)^2\}\)（其中 \(pre\) 为前缀和）。

考虑如何优化。

首先为方便后续计算，令 \(a_i=pre_i+i\)，\(b_i=pre_i+i+L\)，并把 \(L\) 提前 \(+1\)，去掉 \(\min\)。

于是有：\(dp_i=dp_j+(a_i-b_j)^2\)。

展开并移项得：\(dp_j+b_j^2=2a_ib_j+dp_i-a_i^2\)。

把上式中的 \(dp_j+b_j^2\) 看作 \(y\)、\(b_j\) 看作 \(x\)，则：\(y=2a_ix+dp_i-a_i^2\)。

那么此时就珂以把式子看作一条斜率为 \(2a_i\) 的直线。

此时 \(dp_i\) 的几何意义即为：当上述直线经过某点 \(P(b_j,dp_j+b_j^2)\) 时，直线在 \(y\) 轴上的截距 \(+a_i^2\) 的值。

题目就是找截距的最小值。

于是我们可以将该直线从下往上平移找第一个经过的点，此时截距最小。

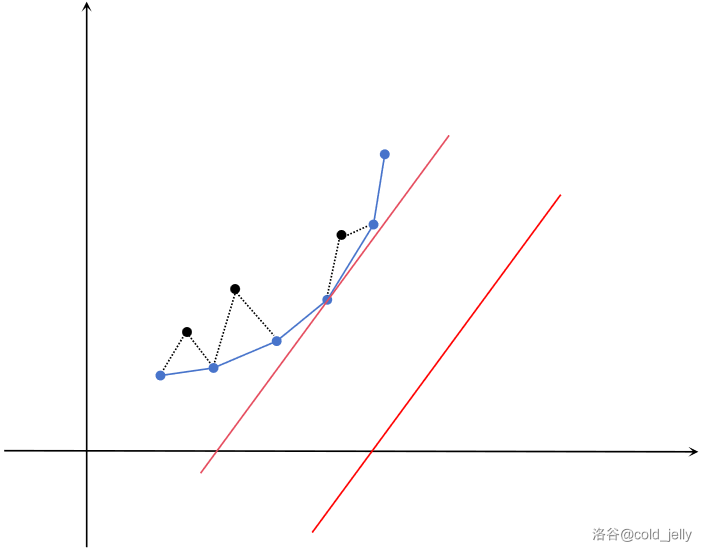
上图中所有点（蓝和黑）代表所有待选决策点，红色直线为目标直线，而容易知道，可能最优的决策点一定位于图中蓝色的下凸包中。

记下凸包相邻两点 \(P_j\) 和 \(P_{j+1}\) 相连直线的斜率为 \(k_j\)，则在下凸包中 \(k\) 是单增的。又目标直线也是单增的，在图像上表现为最优决策点 \(P\) 为满足 \(k_j>2a_i\) 的 \(j\) 最小的点。

由单调性，我们可用单调队列维护凸包，队首的决策点即最优，因此用它转移。

于是得到了本题的 \(O(n)\) 做法。

而对于一般的斜优问题，方法与上述过程类似，具体问题具体分析。

练习：Frog 3。