【数学】学习笔记
Part0 前记
憋了很久,终于下定决心要把【数学】这一部分的知识梳理一遍。本文开始作于 \(2024.11.19\),将从数论、位运算、组合数学、线性代数、概率论、博弈论等板块进行知识的整理,对于例题不过多梳理,定理大都略去证明。
为表达方便,本文中将会采用一些自创符号,将在文中给出解释。
在编写过程中,可能由于作者看百合看傻了,一些笔误还请读者指出。
参考资料:OI wiki、李煜东《算法竞赛进阶指南》。
Part1 数论
数论基础
整除:设 \(a,b\in \mathbf{Z}\),若 \(\exists q\in \mathbf{Z}\) 使得 \(b=aq\),则称 \(b\) 可被 \(a\) 整除,记作 \(a|b\),反之则称 \(b\) 不可被 \(a\) 整除。
约数:若 \(a|b\),则称 \(a\) 是 \(b\) 的约数(因数)。
余数:对于带余除法 \(a\div b=c\text{ reminded }d\),称 \(d\) 是 \(a\) 除以 \(b\) 的余数,记作 \(d=a\mod b\)。对于上面的式子,我们也可等价转化为一个对于解题更有帮助的式子:\(d=a-b\left \lfloor \dfrac{a}{b} \right \rfloor\)。
最大公约数:对于 \(a,b\in \mathbf{Z}\),记 \(\gcd(a,b)\) 表示 \(a,b\) 两数的最大的公共约数,简称为最大公约数,这一定义也可推广到 \(n\) 个数的情形:\(\gcd(a_1,a_2,...,a_n)\)。
最小公倍数:类似于最大公约数,我们记 \(\text{lcm}(a,b)\) 表示 \(a,b\) 两整数的最大的公共倍数,简称为最小公倍数,这一定义也可推广到 \(n\) 个数的情形:\(\text{lcm}(a_1,a_2,...,a_n)\)。
互质:对于 \(a,b\in \mathbf{Z}\),若 \(\gcd(a,b)=1\),则称它们互质。
质数与合数:记 \(m(x)\) 为 \(x\) 的除 \(x\) 和 \(1\) 之外的约数个数,若 \(m(x)=0\),则称 \(x\) 为质数,若 \(m(x)>0\),则称 \(x\) 为合数。特别地,\(1\) 既不是质数又不是合数。
质数的判定法
根据质数的定义,对于数 \(x(x>2)\) 的判定,我们很容易想到的一种思路是 \(2\to x-1\) 遍历,只要有一个数是 \(x\) 的约数,则 \(x\) 是合数,否则是质数。这种做法是 \(O(x)\) 的。
考虑到一个数的约数集合具有除 \(x\) 对称性(即若 \(a|x\),则必有 \(\left(\dfrac{x}{a}\right)|x\)),因此我们只需要枚举 \(2\to \sqrt{x}\) 即可,时间复杂度为 \(O(\sqrt{x})\)。
inline bool isprime(int x)
{
if(x < 2) return false;//特判1
for(int i = 2; i * i <= x; i ++)
if(x % i == 0) return false;
return true;
}
质数的筛法
埃氏筛:
埃氏筛的原理基于这样的思想:对于整数 \(x\),\(2x,3x,...\) 一定不是质数。
给定一个上界 \(N\),我们从 \(2\to N\),对于每一个数 \(x\),标记 \(2x,3x,...,\left \lfloor \dfrac{N}{x} \right \rfloor x\),用一个数组存下来质数即可。
时间复杂度为 \(O(N\log\log N)\)。
const int N = _______;//上界
bool st[N];//标记合数
int p[N], cnt = 0;//记录质数
void Eratosthenes(int x)//埃氏筛
{
memset(st, 0, sizeof st);
for(int i = 2; i <= n; i ++)
{
if(st[i]) continue;
p[++ cnt] = i;
for(int j = i; j <= n / i; j ++)
st[i * j] = true;
}
}
欧拉筛(线性筛):
我们发现埃氏筛仍然会对合数重复标记,所以时间复杂度达不到线性。
线性筛法解决了这一问题,其通过“从大到小累计质因子”的方式标记每个合数。我们用数组 \(v\) 记录最小质因子,在筛选过程中维护 \(v\):
- 依次考虑 \(2\to N\) 之间的每一个数 \(i\);
- 若 \(v_i=0\),则可判定 \(i\in P\)(\(P\) 表示质数集合,下文用此符号代指);
- 扫描不大于 \(v_i\) 的每个质数 \(p\),令 \(v_{i\times p}=p\),这也就是在 \(i\) 的基础上累积一个质因子 \(p\),因为 \(p\leq v_i\),所以 \(p\) 就是 \(i\times p\) 的最小质因子。
按照这样的操作,每一个合数只会被其最小的质因子筛一遍,时间复杂度为 \(O(N)\)。
const int N = _______;
int v[N];//记录最小质因子
int p[N], cnt = 0;//记录质数
void Euler(int n)//线性筛
{
memset(v, 0, sizeof v);
for(int i = 2; i <= n; i ++)
{
if(v[i] == 0)
{
v[i] = i;
p[++ cnt] = i;
}
for(int j = 1; j <= cnt; j ++)
{
if(p[j] > v[i] || p[j] > n / i)
break;
v[i * p[j]] = p[j];
}
}
}
质因数分解
算术基本定理:
任何一个大于 \(1\) 的正整数 \(n\),唯一分解成有限个质数的乘积,可写作:
\(\forall c_i\in \mathbf{Z},\forall p_i\in P\),且 \(p_1<p_2<...<p_m\)。
算术基本定理的推论:
- \(n\) 的正约数集合:\(\displaystyle \{x|x=\prod^{m}_{i=1}p_i^{b_i},0\leq b_i\leq c_i\}\);
- \(n\) 的正约数个数(乘法原理):\(\displaystyle \prod^{m}_{i=1}(c_i+1)\);
- \(n\) 的正约数之和:\(\displaystyle \prod^{m}_{i=1}\sum^{c_i}_{j=0}p_i^j\);
试除法分解质因数:
给定正整数 \(n\),我们遍历 \(i: 2\to \sqrt{n}\),若 \(i|n\),则一直将 \(n\) 除以 \(i\),同时累计对应的次数 \(c\),时间复杂度为 \(O(\sqrt{n})\)。
const int N = _______;
int p[N];//质因子
int c[N];//次数
int m = 0;//记录个数
void div(int n)
{
for(int i = 2; i * i <= n; i ++)
if(n % i == 0)
{
p[++ m] = i, c[m] = 0;
while(n % i == 0) n /= i, c[m] ++;
}
if(n > 1)//特判:n是质数
p[++ m] = i, c[m] = 1;
}
约数
试除法求正约数集合:
对于正整数 \(n\),如何求它的正约数集合呢?
我们知道约数的这样一个性质:若 \(a|x\),则必有 \(\left(\dfrac{x}{a}\right)|x\),因此我们可以通过判定质数的类似的方法来求正约数集合。
考虑扫描 \(i: 1\to \sqrt{n}\),若 \(i|n\),则 \(\dfrac{n}{i}\) 也是 \(n\) 的约数。需要注意,若 \(i^2=n\),此时如果不加特判,则 \(i\) 会被重复记录,这里需要加上特判,具体见代码实现:
const int N = _______;
int f[N], cnt = 0;//记录约数
void factor(int n)
{
for(int i = 1; i * i <= n; i ++)
if(n % i == 0)
{
f[++ cnt] = i;
if(i != n / i) f[++ cnt] = n / i;
}
}
根据试除法,我们可以得出一个基本事实:\(n\) 的约数个数不超过 \(2\sqrt{n}\)。
求两数的最大公约数
由于 CCF 在某年开始允许使用下划线开头的系统库函数,因此我们可直接调用 __gcd(a,b) 函数来求 \(a\),\(b\) 两数的最大公约数。
但我们还是需要了解求最大公约数的两种算法。
更相减损术:
定理:\(\forall a,b\in \mathbf{N},b\leq a\),有 \(\gcd(a,b)=\gcd(b,a-b)=\gcd(a,a-b)\)。
根据定理,我们可以通过递归方式求两数的最大公约数。
欧几里得算法:
定理:\(\forall a,b\in \mathbf{N},b\ne 0\),有 \(\gcd(a,b)=\gcd(a,a\mod b)\)。
使用欧几里得算法是更为常用的求最大公约数的方法,但是对于高精度 GCD,由于高精度除法(取模)实现较为复杂,所以此时可以考虑用更相减损术代替欧几里得算法。
欧几里得算法求最大公约数的时间复杂度为 \(O(\log\max(a,b))\)。
int gcd(int a, int b)//欧几里得算法
{
return b ? gcd(b, a % b) : a;
}
扩展欧几里得算法(exgcd)
裴蜀定理:\(\forall a,b\in \mathbf{Z},\exists x,y\in \mathbf{Z}\),满足 \(ax+by=\gcd(a,b)\)。
证明:在欧几里得算法的最后一步,即 \(b=0\) 时,显然有 \(x=1,y=0\),使得式子成立。
当 \(b>0\) 时,则 \(\gcd(a,b)=\gcd(b,a\mod b)\),假设存在 \(x,y\in \mathbf{Z}\) 满足 \(bx+(a\mod b)y=\gcd(b,a\mod b)\),因为 \(bx+(a\mod b)y=bx+\left( a-b\left \lfloor \dfrac{a}{b} \right \rfloor \right)y=ay+b\left( x-\left \lfloor \dfrac{a}{b} \right \rfloor y \right)\),所以令 \(x^{'}=y\),\(y^{'}=x-\left \lfloor \dfrac{a}{b} \right \rfloor y\),就得到了 \(ax^{'}+by^{'}=\gcd(a,b)\)。
由数学归纳法可得定理成立。
上述证明中给出了 \(x\) 和 \(y\) 的计算方法,称为扩展欧几里得算法(exgcd),通过代码实现,我们可以通过 exgcd 计算两数 \(a,b\) 的最大公约数 \(d\)。
int exgcd(int a, int b, int &x, int &y)
{
if(b == 0)
{
x = 1, y = 0;
return a;
}
int d = exgcd(b, a % b, x, y);
int z = x;
x = y, y = z - y * (a / b);
return d;
}
求两数的最小公倍数
定理:\(\forall a,b\in \mathbf{N}\),有 \(\gcd(a,b)\times \text{lcm}(a,b)=ab\)。
根据定理,我们可以通过最大公约数求得最小公倍数:
int lcm(int a, int b)
{
return a / gcd(a, b) * b;
}
注意,在代码中我们先除后乘,这防止了乘法带来的可能的溢出,这是求解很多题目中需要注意的细节及小技巧。
欧拉函数
定义:将 \(1\to x\) 中与 \(x\) 互质的数的个数称为欧拉函数,记作 \(\varphi(x)\)。
在算术基本定理分解下,设 \(\displaystyle n=\prod^{m}_{i=1}p_{i}^{c_i}\),则有欧拉函数的计算公式:
求欧拉函数:
根据上述计算公式,我们只需要对数进行质因数分解,即可求得该数的欧拉函数值:
int phi(int n)//φ(n)
{
int ans = n;
for(int i = 2; i * i <= n; i ++)
if(n % i == 0)
{
ans = ans / i * (i - 1);
while(n % i == 0) n /= i;
}
if(n > 1) ans = ans / n * (n - 1);
return ans;
}
欧拉函数的性质:
- \(\forall n>1\),\(\displaystyle \sum^{n}_{i=1,\gcd(i,n)=1}i=\dfrac{n\times \varphi(n)}{2}\);
- 若 \(\gcd(a,b)=1\),则 \(\varphi(ab)=\varphi(a)\varphi(b)\);
- \(\forall p\in P\),若 \(p|n\) 且 \(p^2|n\),则 \(\varphi(n)=\varphi\left( \dfrac{n}{p} \right)\times p\);
- \(\forall p\in P\),若 \(p|n\) 且 \(p^2\nmid n\),则 \(\varphi(n)=\varphi\left( \dfrac{n}{p} \right)\times (p-1)\);
- \(\displaystyle \sum_{i|n}\varphi(i)=n\);
- \(\forall p\in P,\forall a\in \mathbf{Z}_+\),有 \(\varphi(p^a)=(p-1)p^{a-1}\)。
线性筛求欧拉函数:
根据欧拉函数的有关性质,我们可以在线性时间复杂度内求得给定上界 \(N\) 内所有数的欧拉函数值。
const int N = _______;
int phi[N], n;//φ(n)
int p[N], cnt;//质数
bool st[N];
inline void findphi()
{
phi[1] = 1, p[1] = 0;
for(int i = 2; i <= n; i ++)
{
if(!st[i])
{
p[++ cnt] = i;
phi[i] = i - 1;//性质6
}
for(int j = 1; j <= cnt && i * p[j] <= n; j ++)
{
v[i * p[j]] = true;
if(i % p[j] == 0)//性质3
{
phi[i * p[j]] = phi[i] * p[j];
break;
}
else phi[i * p[j]] = phi[i] * (p[j] - 1);//性质4
}
}
}
同余及相关定理
定义:若 \(a,b\in \mathbf{Z}\),满足 \(a\mod m=b\mod m\),则称 \(a,b\) 模 \(m\) 同余,记作 \(a\equiv b\pmod{m}\)。
同余类:\(\forall a\in [0,m-1]\),集合 \(\{x|x=a+km,k\in \mathbf{Z}\}\) 中的所有元素模 \(m\) 同余,余数为 \(a\),该集合被称为一个模 \(m\) 的同余类,记作 \(\bar{a}\)。
剩余系:模 \(m\) 的所有同余类构成的集合:\(\{\bar{0},\bar{1},\bar{2},...,\overline{m-1}\}\) 被称作 \(m\) 的完全剩余系;其中与 \(m\) 互质的数所代表的同余类共有 \(\varphi(m)\) 个,它们构成 \(m\) 的简化剩余系。
费马小定理:\(\forall p\in P,\forall a\in \mathbf{Z}\),有 \(a^p\equiv a\pmod{p}\)。
欧拉定理:\(\forall a,n\in \mathbf{Z}_{+}\),若 \(\gcd(a,n)=1\),则有结论:\(a^{\varphi(n)}\equiv 1\pmod{n}\)。
欧拉定理推论:\(\forall a,n,b\in \mathbf{Z}_{+}\),若 \(\gcd(a,n)=1\),有 \(a^b\equiv a^{b\mod \varphi(n)}\pmod{n}\)。
扩展欧拉定理:\(\forall b\ge \varphi(p)\),有 \(a^b\equiv a^{b\mod \varphi(p)+\varphi(p)}\pmod p\),其中不要求 \(a\),\(p\) 互质。
威尔逊定理:\(\forall p\in P\),\((p-1)!\equiv -1\pmod{p}\),其中 \(n!\) 表示 \(n\) 的阶乘,即 \(\displaystyle n!=\prod^{n}_{i=1}i\)。
莫比乌斯函数
设正整数 \(n\) 按照算术基本定理分解为 \(\displaystyle n=\prod^{m}_{i=1}p_i^{c_i}\),定义函数
称 \(\mu(n)\) 为莫比乌斯函数。
说人话就是,当 \(n\) 包含相等的质因子时,\(\mu(n)=0\)。当 \(n\) 的所有质因子各不相等时,若 \(n\) 有偶数个质因子,\(\mu(n)=1\);否则 \(\mu(n)=-1\)。
求 \(1\to N\) 中每个数的莫比乌斯函数值可以利用埃氏筛计算。把所有莫比乌斯函数值初始化为 \(1\),接下来对于筛出来的每一个质数 \(p\),令 \(\mu(p)=-1\),并扫描 \(p\) 的倍数 \(x\),检查 \(x\) 是否能被 \(p^2\) 整除。若能,则令 \(\mu(x)=0\),否则令 \(\mu(x)=-\mu(x)\)。
const int N = _______;
int miu[N], n;//μ(n)
int st[N];//标记
void init()//初始化
{
for(int i = 1; i <= n; i ++)
miu[i] = 1, st[i] = false;
}
void mobius()
{
init();
for(int i = 2; i <= n; i ++)
{
if(st[i]) continue;
miu[i] = -1;
for(int j = i * 2; j <= n; j += i)//埃氏筛
{
st[j] = true;
if((j / i) % i == 0) miu[j] = 0;
else miu[j] *= -1;
}
}
}
乘法逆元
定义:若 \(\gcd(b,m)=1\) 且 \(b|a\),则 \(\exists x\in \mathbf{Z}\),使得 \(\dfrac{a}{b}\equiv a\times x\pmod{m}\),则称 \(x\) 为 \(b\) 的模 \(m\) 乘法逆元,记作:\(b^{-1}(\mod m)\)。
根据费马小定理,若 \(m\in P\),则 \(b^{m-2}\) 就是 \(b\) 的乘法逆元。
在保证 \(\gcd(b,m)=1\) 的前提下,乘法逆元可通过求解同余方程 \(bx\equiv 1\pmod{m}\) 得到。
题意:给定 \(a,b\),求关于 \(x\) 的同余方程 \(ax\equiv 1\pmod{b}\) 的最小正整数解,数据保证一定有解。
分析:这里插入一个有关线性同余方程的知识:线性同余方程 \(ax\equiv b\pmod{m}\)有解当且仅当 \(\gcd(a,m)=b\)。
根据上述结论,题目中给出的同余方程有解这一条件可等价转化为 \(\gcd(a,b)=1\),即 \(a,b\) 互质,方程可改写为 \(ax+by=1\),用扩展欧几里得算法求出一组特解 \(x_0,y_0\),则 \(x_0\) 就是原方程的一个解,通解集合就是 \(\{x|x\equiv x_0\pmod{b},x\in \mathbf{Z}\}\)。通过取模操作把解的范围 \(\to [1,b]\),就得到了最小正整数解。
代码如下(记得开 long long):
#include<bits/stdc++.h>
#define int long long
using namespace std;
int exgcd(int a, int b, int &x, int &y)
{
if(b == 0)
{
x = 1, y = 0;
return a;
}
int m = exgcd(b, a % b, x, y);
int z = x;
x = y;
y = z - y * (a / b);
return m;
}
signed main()
{
int a, b, x, y;
cin >> a >> b;
exgcd(a, b, x, y);
cout << (x % b + b) % b;
return 0;
}
中国剩余定理(CRT)
设 \(m_1,m_2,...,m_n\) 是两两互质的整数,设 \(\displaystyle m=\prod^{n}_{i=1}m_i\),\(M_i=\dfrac{m}{m_i}\),\(t_i\) 是线性同余方程 \(M_it_i\equiv 1\pmod{m_i}\) 的一个解。对于任意的 \(n\) 个整数 \(a_1,a_2,...,a_n\),方程组
有整数解 \(\displaystyle x=\sum^{n}_{i=1}a_iM_it_i\)。
上述定理被称为中国剩余定理(CRT),其给出了方程组的一个特解,方程组的通解集合为 \(\{y|y=x+km,k\in \mathbf{Z}\}\),若要求出最小的非负正整数解,只需把 \(x\) 对 \(m\) 取模,使得 \(x\) 落在 \([0,m-1]\) 上即可。
int CRT(int k, int *a, int *r)
{
int n = 1, ans = 0;
for(int i = 1; i <= k; i ++) n = n * r[i];
for(int i = 1; i <= k; i ++)
{
int m = n / r[i], b, y;
exgcd(m, r[i], b, y);
ans = (ans + a[i] * m * b % n) % n;
}
return (ans % n + n) % n;
}
扩展中国剩余定理(exCRT)
在中国剩余定理中,我们规定了 \(m_1,m_2,...,m_n\) 是两两互质的整数,不能解决模数不两两互质的情况,在这时我们就需要扩展中国剩余定理(exCRT)。
内容:与 CRT 类似,我们的目的是求解方程组\(\displaystyle \begin{cases}x\equiv a_1\pmod{m_1}\\x\equiv a_2\pmod{m_2}\\...\\x\equiv a_n\pmod{m_n}\end{cases}\),但此时并没有 \(m_1,m_2,...,m_n\) 两两互质这一条件。考虑如何将两方程合并为一个,考虑将 \(x\) 写成两个含待定系数方程的形式,则可列等式,发现是一个不定方程的形式,先用裴蜀定理判无解,再用扩展欧几里得算法求一组特解,回代求出一个特定的 \(x\),那么新的 \(m=\text{lcm}(m_1,m_2)\),\(a=x\mod m\)。
关于 exCRT,可以去看这道例题:P4777。
Lucas 定理
声明:现在数学界对于组合数(\(n\) 选 \(m\))的写法通常采用 \(\displaystyle \binom{n}{m}\) 而非 \(\text{C}^{m}_{n}\),本文统一采用前者。
内容:\(\forall p\in P\),有 \(\displaystyle \binom{n}{m}\mod p=\displaystyle \binom{\left \lfloor n/p \right \rfloor}{\left \lfloor m/p \right \rfloor}\times \binom{n\mod p}{m\mod p}\mod p\)。
Lucas 定理常用于解决大组合数取模的问题。
int Lucas(int n, int m, int p)
{
if(m == 0) return 1;
return (C(n % p, m % p, p) * Lucas(n / p, m / p, p)) % p;
}
数论分块
数论分块可以快速计算一些含有除法向下取整的和式(形如 \(\displaystyle \sum^{n}_{i=1}f(i)g\left( \left \lfloor \dfrac{n}{i} \right \rfloor\right)\) 的和式)。当可以在 \(O(1)\) 内计算 \(f(r)-f(l)\) 或已经预处理出 \(f\) 的前缀和时,数论分块就可以在 \(O(\sqrt{n})\) 的时间内计算上述和式的值。
数论分块的原理是把 \(\left \lfloor \dfrac{n}{i} \right \rfloor\) 相同的数打包同时计算。
几条引理及结论:
\(\forall a,b,c\in \mathbf{Z},\left \lfloor \dfrac{a}{bc} \right \rfloor=\left \lfloor \dfrac{\left \lfloor \frac{a}{b} \right \rfloor}{c} \right \rfloor\)。
\(\forall n\in \mathbf{N}_{+},\left | \left \{ \left \lfloor \dfrac{n}{d} \right \rfloor \right \}|d\in \mathbf{N}_{+},d\le n \right |\le \left |\left \lfloor 2\sqrt{n} \right \rfloor\right |\)。
数论分块结论:对于常数 \(n\),使得式子 \(\left\lfloor\dfrac{n}{i}\right\rfloor=\left\lfloor\dfrac{n}{j}\right\rfloor\) 成立且满足 \(i\le j\le n\) 的 \(j\) 值最大为 \(\left\lfloor\dfrac n{\lfloor\frac ni\rfloor}\right\rfloor\),即值 \(\left\lfloor\dfrac ni\right\rfloor\) 所在块的右端点为 \(\left\lfloor\dfrac n{\lfloor\frac ni\rfloor}\right\rfloor\)。
数论分块过程:
考虑和式 \(\displaystyle \sum^{n}_{i=1}f(i)\left \lfloor \dfrac{n}{i}\right \rfloor\)。由于 \(\left \lfloor \dfrac{n}{i}\right \rfloor\) 的值成块状分布,那么就可以用数论分块加速计算,降低算法时间复杂度。
具体地,我们先求出 \(f(i)\) 的前缀和(记作 \(\displaystyle s(i)=\sum^{i}_{j=1}f(j)\)),然后每次以 \([l,r]=\left[l,\left\lfloor\dfrac n{\lfloor\frac ni\rfloor}\right\rfloor\right]\) 为一块,分块求出贡献累加到结果中即可。
题意:给定 \(n\) 和 \(k\),求:
的值。
分析:暴力枚举 TLE,不妨先观察式子,进行变形再找到更优的算法。
不妨展开式子:
由公式 \(a\mod b=a-b\left \lfloor \dfrac{a}{b}\right \rfloor\) 可知:
于是我们可以将 \(ans\) 初始化为 \(nk\),再减去后面的和式即可。
而我们可以发现后面的式子就是一个标准的数论分块式子,利用数论分块的基本原理即可快速求解。
\(\left \lfloor \dfrac{k}{i}\right \rfloor\) 的取值大约有 \(\sqrt{k}\) 种,故时间复杂度为 \(O(\sqrt{k})\)。
代码如下:
#include<bits/stdc++.h>
#define int long long
using namespace std;
int n, k, ans;
signed main()
{
cin >> n >> k;
ans = n * k;
for(int l = 1, r; l <= n; l = r + 1)
{
if(k / l == 0) break;
r = min(k / (k / l), n);
ans -= (k / l) * (l + r) * (r - l + 1) / 2;
}
cout << ans;
return 0;
}
Part2 位运算
进制与进制转换
进制:
我们在生活中最常使用的数为十进制数,而计算机使用二进制数。所谓 \({n}\) 进制数,就是在该进制下的数“逢 \(n\) 进 \(1\)”。例如,在十进制数体系下,逢 \(10\) 进 \(1\),因此该数系下的数位符号(数字)集合为 \(\{0,1,2,3,4,5,6,7,8,9\}\);而在二进制数体系下,逢 \(2\) 进 \(1\),因此该数系下的数位符号(数字)集合为 \(\{0,1\}\)。
相同数字在不同进制下的表达方式通常不同。例如在十进制下数字 \(10\) 在二进制表示下为 \(1010\),而二进制下的“\(10\)”表示数字 \(2\)。
因此为了避免混淆,我们采用将数字括起来,并在右下角写上进制数的方式表达数字:
常用的进制有:十进制、二进制、八进制、十六进制,它们分别表示 \(0\)~\(16\) 数字如下表所示:
| 进制数 | \(10\) | \(2\) | \(8\) | \(16\) |
|---|---|---|---|---|
| \(0\) | \((0)_{10}\) | \((0)_2\) | \((0)_8\) | \((0)_{16}\) |
| \(1\) | \((1)_{10}\) | \((1)_2\) | \((1)_8\) | \((1)_{16}\) |
| \(2\) | \((2)_{10}\) | \((10)_2\) | \((2)_8\) | \((2)_{16}\) |
| \(3\) | \((3)_{10}\) | \((11)_2\) | \((3)_8\) | \((3)_{16}\) |
| \(4\) | \((4)_{10}\) | \((100)_2\) | \((4)_8\) | \((4)_{16}\) |
| \(5\) | \((5)_{10}\) | \((101)_2\) | \((5)_8\) | \((5)_{16}\) |
| \(6\) | \((6)_{10}\) | \((110)_2\) | \((6)_8\) | \((6)_{16}\) |
| \(7\) | \((7)_{10}\) | \((111)_2\) | \((7)_8\) | \((7)_{16}\) |
| \(8\) | \((8)_{10}\) | \((1000)_2\) | \((10)_8\) | \((8)_{16}\) |
| \(9\) | \((9)_{10}\) | \((1001)_2\) | \((11)_8\) | \((9)_{16}\) |
| \(10\) | \((10)_{10}\) | \((1010)_2\) | \((12)_8\) | \((A)_{16}\) |
| \(11\) | \((11)_{10}\) | \((1011)_2\) | \((13)_8\) | \((B)_{16}\) |
| \(12\) | \((12)_{10}\) | \((1100)_2\) | \((14)_8\) | \((C)_{16}\) |
| \(13\) | \((13)_{10}\) | \((1101)_2\) | \((15)_8\) | \((D)_{16}\) |
| \(14\) | \((14)_{10}\) | \((1110)_2\) | \((16)_8\) | \((E)_{16}\) |
| \(15\) | \((15)_{10}\) | \((1111)_2\) | \((17)_8\) | \((F)_{16}\) |
| \(16\) | \((16)_{10}\) | \((10000)_2\) | \((20)_8\) | \((10)_{16}\) |
十进制转 \(n\) 进制:
原理:对于十进制下的数 \(x\),对其反复除 \(n\) 取余,将所有余数倒序统计得到该数在 \(n\) 进制下的表示。
具体过程(将 \((x)_{10}\) 转化为 \((x)_{n}\)):
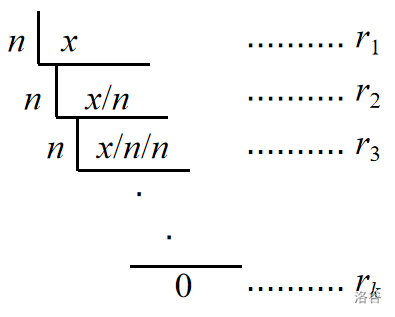
那么 \((x)_{10}=(\overline{r_k...r_3r_2r_1})_{n}\)。
这种方法被称为辗转相除法。
例如,要将 \((19)_{10}\) 分别转化为二进制和十六进制:
-
转二进制:\(19\div 2=9\text{ reminded }1\);\(9\div 2=4\text{ reminded }1\);\(4\div 2=2\text{ reminded }0\);\(2\div 2=1\text{ reminded }0\);\(1\div 2=0\text{ reminded }1\)。故 \((19)_{10}=(10011)_{2}\);
-
转十六进制:\(19\div 16=1\text{ reminded }3\);\(1\div 16=0\text{ reminded }1\)。故 \((19)_{10}=(13)_{16}\)。
用代码实现如下:
const int N = _______;
char num[17] = {'0', '1', '2', '3', '4', '5', '6', '7', '8', '9', 'A', 'B', 'C', 'D', 'E', 'F'};//数字表
char ans[N], cnt;//答案
void work(int x, int n)//将十进制数x转化为n进制
{
while(x)//辗转相除
{
ans[++ cnt] = num[x % n];
x /= n;
}
for(int i = cnt; i >= 1; i --)//倒序输出
printf("%c", ans[i]);
}
\(n\) 进制转十进制:
原理:设 \(n\) 进制数的第 \(i\) 位数值为 \(a_i\)(倒序,且下标从 \(0\) 开始),则其对十进制下该数的值产生 \(a_i\times n^i\) 的贡献。
用公式表达就是:
例如,要将 \((10011)_{2}\) 转化为十进制,由公式可知:\(\displaystyle (10011)_{2}=\left[\sum^{4}_{i=0}(a_i\times 2^i)\right]_{10}=(2^4+2^1+2^0)_{10}=(19)_{10}\)。
用代码实现如下:
const int N = _______;
char cnt, x[N];
int ans;//答案
void work(int n)//n进制转十进制
{
cin >> x;
cnt = strlen(x);
for(int i = 0; i < cnt; i ++)
{
if(x[i] >= '0' && x[i] <= '9')
{
ans += (x[i] - 48) * pow(n, cnt - i - 1);
}
else//'A'~'F'
ans += (x[i] - 55) * pow(n, cnt - i - 1);
}
cout << ans;
}
按位与、或、非、异或运算
位运算:计算机对二进制数的运算被称为位运算。
按位与:
按位与运算,指对两二进制数 \((a)_{2}\),\((b)_{2}\) 按照位数对齐后对于每一位数(\(0\) 或 \(1\))依照逻辑与运算法则(\(0\&X=0\),\(1\&1=1\))运算得到结果的运算,通常用符号 \(\&\) 或 \(\text{and}\) 表示按位与运算,例如:\(a\&b\)、\(a\text{ and }b\),而在 C++ 中实现为 a&b。
具体地说,假设 \((a)_2=\overline{a_1a_2a_3...a_n}\),\((b)_2=\overline{b_1b_2b_3...b_n}\)(已做高位补 \(0\) 处理),考虑第 \(i\) 位 \(a_i\) 与 \(b_i\),经过法则得到结果 \(c_i\)。按位与运算的结果即为 \((a)_{2}\&(b)_{2}=(c)_{2}=\overline{c_1c_2c_3...c_n}\)。
例如,计算 \((6)_{10}\&(11)_{10}\) 的过程如下:
按位与运算实质上是在对于两二进制数加法运算时仅保留进位的一位的 \(1\) 的运算。
按位或:
按位或运算,指对两二进制数 \((a)_{2}\),\((b)_{2}\) 按照位数对齐后对于每一位数(\(0\) 或 \(1\))依照逻辑或运算法则(\(1|X=1\),\(0|0=0\))运算得到结果的运算,通常用符号 \(|\) 或 \(\text{or}\) 表示按位或运算,例如:\(a|b\)、\(a\text{ or }b\),而在 C++ 中实现为 a|b。
具体地说,假设 \((a)_2=\overline{a_1a_2a_3...a_n}\),\((b)_2=\overline{b_1b_2b_3...b_n}\)(已做高位补 \(0\) 处理),考虑第 \(i\) 位 \(a_i\) 与 \(b_i\),经过法则得到结果 \(c_i\)。按位与运算的结果即为 \((a)_{2}|(b)_{2}=(c)_{2}=\overline{c_1c_2c_3...c_n}\)。
例如,计算 \((6)_{10}|(11)_{10}\) 的过程如下:
按位或运算实质上是在对于两二进制数加法运算时仅少保留进位的一位数字 \(1\) 的运算。
按位异或:
按位异或运算,指对两二进制数 \((a)_{2}\),\((b)_{2}\) 按照位数对齐后对于每一位数(\(0\) 或 \(1\))依照逻辑异或运算法则(\(X\oplus X=0\),\(X\oplus(\neg X)=1\))运算得到结果的运算,通常用符号 \(\oplus\) 或 \(\text{xor}\) 表示按位异或运算,例如:\(a\oplus b\)、\(a\text{ xor }b\),而在 C++ 中实现为 a^b。
具体地说,假设 \((a)_2=\overline{a_1a_2a_3...a_n}\),\((b)_2=\overline{b_1b_2b_3...b_n}\)(已做高位补 \(0\) 处理),考虑第 \(i\) 位 \(a_i\) 与 \(b_i\),经过法则得到结果 \(c_i\)。按位与运算的结果即为 \((a)_{2}\oplus(b)_{2}=(c)_{2}=\overline{c_1c_2c_3...c_n}\)。
例如,计算 \((6)_{10}\oplus(11)_{10}\) 的过程如下:
按位异或运算实质上是对于两二进制数的不进位加法。
按位非:
与按位与、或、异或运算不同,按位非运算是一元运算,其运算功效是将二进制数的每一位反转为异性数(\(0\to 1\),\(1\to 0\))。按位非运算的符号为 \(\neg a\),而在 C++ 中实现为 ~a。
移位运算
左移:
在二进制表示下把数字同时向左移动,低位用 \(0\) 填充,高位越界后舍去的运算称为左移运算,符号为 \(<<\),而在 C++ 中实现为 a<<b。
有公式:
算术右移:
在二进制补码表示下把数字同时向右移动,高位以符号位填充,低位越界后舍去的运算称为算术右移运算,符号为 \(>>\),而在 C++ 中实现为 a>>b。
有公式:
快速幂:
位运算有许多应用,其中一种就是快速幂的实现。
考虑这样一个问题:如何求出 \(a^b\mod p\) 的值呢?一种朴素的做法是直接将 \(a\) 自乘 \(b\) 次,时间复杂度为 \(O(b)\)。但一旦 \(b\) 的范围过大,该算法的复杂度较劣。我们需要一种更快捷的算法,即快速幂。
根据数学常识,如果 \(b\) 在二进制下表示有 \(k\) 位,其中第 \(i\) 位的数字是 \(c_i\),那么有 \(b=\displaystyle \sum^{k}_{j=1}\left( c_{k-j}\times 2^{k-j}\right)\)。于是有:\(\displaystyle a^b=\prod^{k}_{j=1}a^{c_{k-j}\times 2^{k-j}}\)。又因为 \(k=\left \lceil \log_2(b+1) \right \rceil\),所以上式的乘积项数量不多于 \(\left \lceil \log_2(b+1) \right \rceil\) 个。又有 \(a^{2^i}=\left( a^{2^{i-1}}\right)^2\),所以我们很容易通过 \(k\) 次递推求出每个乘积项,当 \(c_i=1\) 时,累积答案。\(b\& 1\) 运算能够取出 \(b\) 在二进制表示下的最低位,而 \(b>>1\) 运算可以舍去最低位,二者反复循环,就可以遍历所有 \(c_i\),算法时间复杂度为 \(O(\log b)\)。
代码如下:
inline int qp(int a, int b, int p)//a^b mod p
{
int res = 1;
while(b)
{
if(b & 1) res = res * a % p;
a = a * a % p;
b >>= 1;
}
return res;
}
提醒:\(\color{red}\text{位运算的优先级极低,在不确定的情况下一定要加上括号防止出错。}\)
其他运算或函数
lowbit 运算:
函数 \(\text{lowbit}(n)\) 定义为非负整数 \(n\) 在二进制表示下“最低位的 \(1\) 及其后边所有的 \(0\)”构成的数值。例如,\(n=(10)_{10}\) 的二进制表示为 \((1010)_2\),则 \(\text{lowbit}(n)=(10)_2=(2)_{10}\)。
有公式:
代码实现为:
inline int lowbit(int n)
{
return n & (-n);
}
lowbit 运算在很多问题中有实际应用,特别地,其还是实现树状数组的一个基本运算。
popcount 运算:
函数 \(\text{popcount}(n)\) 定义为非负整数 \(n\) 在二进制表示下有多少位为 \(1\)。例如,\(n=(10)_{10}\) 的二进制表示为 \((1010)_2\),则 \(\text{popcount}(n)=2\)。
利用 C++ 内置的库函数 __built_popcount(unsigned int n) 可以求出 \(\text{popcount}(n)\),另一个库函数 __built_popcount(unsigned long long n) 作用相同,只是范围扩大到了 unsigned long long。
手动实现 popcount 运算代码如下:
inline int popcount(int n)
{
int res = 0;
while(n)
{
if(n & 1) res ++;
n >>= 1;
}
return res;
}
位运算的性质
交换律:\(a\& b=b\& a\),\(a|b=b|a\),\(a\oplus b=b\oplus a\)。
结合律:\(a\& b\& c=a\& (b\& c)\),\(a|b|c=a|(b|c)\),\(a\oplus b\oplus c=a\oplus (b\oplus c)\)。
恒等律:\(a|0=a\),\(a\oplus 0=a\),\(a\& a=a\),\(a|a=a\)。
归零律:\(a\& 0=0\),\(a\oplus a=0\)。
自反律:\(\neg(\neg a)=a\),\(a\oplus a\oplus a=a\)。
分配律:\(a\& (b|c)=(a\& b)|(a\& c)\),\(a|(b\& c)=(a|b)\& (a|c)\),\(a\& (b\oplus c)=(a\& b)\oplus (a\& c)\)。
吸收律:\(a|(a\& b)=a\),\(a\& (a|b)=a\)。
摩根定律:\(\neg (a\& b)=(\neg a)|(\neg b)\),\(\neg (a|b)=(\neg a)\& (\neg b)\)。
异或展开:\(a\oplus b=(a\& b)\oplus (a|b)\)。
异或和:\(\displaystyle \bigoplus^{n}_{i=1}i=\left\{\begin{matrix} 1 & n\equiv 1\pmod{4}\\ n+1 & n\equiv 2\pmod{4}\\ 0 & n\equiv 3\pmod{4}\\ n & 4|n \end{matrix}\right.\)
加法展开:\(a+b=(a\& b)+(a|b)\),\(a+b=2(a\& b)+(a\oplus b)\)。
异或等价:\(a\oplus b=0\Longrightarrow a=b\)。
成对变换:\(n\oplus 1=\left\{\begin{matrix} n+1 & 2|n\\ n-1 & \text{otherwise} \end{matrix}\right.\)。
位运算不等式:
1.\(a\& b\le \max(a,b)\);
2.\(a\oplus b\ge a-b\),当且仅当 \(a\& b=b\) 时取等。
奇偶性:\(n\& 1=\left\{\begin{matrix} 0 & 2|n\\ 1 & \text{otherwise} \end{matrix}\right.\)。
\(2\) 的幂次:\(2^n=1<<n\)。
lowbit 相关:1.\(a|(-a)=-\text{lowbit}(a)\);2.\(a\oplus (-a)=-\text{lowbit}(a)<<1\)。
二进制数与 bitset
bitset 是 C++ 内置的一种 STL 容器,可看作一个多位二进制数,每 \(8\) 位占用 \(1\) 字节,相当于采用了状态压缩的二进制数组,并支持基本的位运算。\(n\) 位 bitset 执行一次位运算的复杂度可视为 \(\dfrac{n}{32}\),效率较高。
bitset 的声明:
const int N = _______;
bitset<N> s;
表示声明一个 \(N\) 位二进制数 \(s\)。
操作符:
代码 s[k] 表示访问 \(s\) 的第 \(k\) 位。
对于 bitset 的位运算,与变量的位运算的写法一致。
方法函数:
s.count():返回 \(s\) 有多少位为 \(1\);
s.any():若 \(s\) 所有位都为 \(0\),则返回 false,否则返回 true;
s.none():若 \(s\) 所有位都为 \(0\),则返回 true,否则返回 false;
s.set():把 \(s\) 的所有位变为 \(1\);
s.reset():把 \(s\) 的所有位变为 \(0\)。
Part3 组合数学
加法原理和乘法原理
加法原理:对于“分类”计数,若每一类方法之间互不重合,则总方案数为子方法数之和。
乘法原理:对于“分步”计数,若每一类方法之间互相独立,则总方案数为子方法数之积。
排列数
从 \(n\) 个不同元素中依次取出 \(m\) 个元素排成一列,产生的不同排列的数量为:
其中 \(\text{A}^{m}_{n}\)(\(\text{P}^{m}_{n}\))叫做排列数。
阶乘:
上述式子中我们采用了形如 \(n!\) 的符号,它表示 \(n\) 的阶乘,阶乘的计算公式为:\(n!=\displaystyle \prod^{n}_{i=1}i\)。特别地,规定 \(0!=1\)。
全排列:
在排列数的计算公式中,如果 \(n=m\),即从 \(n\) 个不同元素中依次取出 \(n\) 个元素排成一列的方案数,此时我们将其称为 \(n\) 的一个全排列,有公式 \(\text{A}^{n}_{n}=n!\)。递归求一个数的全排列的代码如下(例题:link):
#include<bits/stdc++.h>
using namespace std;
int n;
vector<int> path;
void dg(int u, int state)
{
if(u == n)
{
for(auto x : path) printf("%d ", x);
printf("\n");
return;
}
for(int i = 0; i < n; i ++)
if(!(state >> i & 1))
{
path.push_back(i + 1);
dg(u + 1, state | (1 << i));
path.pop_back();
}
}
int f(int n)//记录方案总数,即n!
{
int sum = 1;
for(int i = 1; i <= n; i ++)
sum *= i;
return sum;
}
int main()
{
scanf("%d", &n);
dg(0, 0);
cout << f(n);
return 0;
}
组合数及其性质
从 \(n\) 个元素中取出 \(m\) 个元素组成一个集合(不考虑顺序),产生不同的集合数量为:
其中 \(\displaystyle \binom{n}{m}\) 叫做组合数,读作「\(n\) 选 \(m\)」。
组合数的部分性质:
- \(\displaystyle \binom{n}{m}=\displaystyle \binom{n}{n-m}\);
- 递推公式:\(\displaystyle \binom{n}{m}=\displaystyle \binom{n-1}{m}+\displaystyle \binom{n-1}{m-1}\);
- \(\displaystyle \sum^{n}_{i=0}\binom{n}{i}=2^n\);
- \(\displaystyle \sum^{n}_{i=0}\binom{n-i}{i}=Fib(n+1)\),其中 \(Fib(n)\) 表示斐波那契数列的第 \(n\) 项;
- \(\displaystyle \binom{n}{m}=\dfrac{n}{m}\binom{n-1}{m-1}\);
- \(\displaystyle \sum^{n}_{i=0}(-1)^i\binom{n}{i}=[n=0]\),其中 \([P]\) 为艾佛森括号,当命题 \(P\) 为真时值为 \(1\),否则为 \(0\);
- 范德蒙德卷积:\(\displaystyle \sum^{m}_{i=0}\binom{n}{i}\binom{m}{k-i}=\binom{m+n}{k}\);
- 上指标求和:\(\displaystyle \sum_{l=0}^n\binom{l}{k}=\binom{n+1}{k+1}\);
- \(\displaystyle \binom{n}{r}\binom{r}{k}=\binom{n}{k}\binom{n-k}{r-k}\);
- 吸收公式:\(\displaystyle r\binom{r-1}{k-1}=k\binom{r}{k}\)。
组合数的求法
如何代码实现求组合数 \(\displaystyle \binom{n}{m}\) 呢?
朴素暴力:
int C(int n, int m)
{
int res = 1;
for(int i = 1; i <= m; i ++)
res = res * (a - i + 1) / i;
return res;
}
预处理阶乘:
根据公式 \(\displaystyle \binom{n}{m}=\dfrac{n!}{m!(n-m)!}\),一种直接的方法是先预处理阶乘数组 \(fac\),直接代入公式计算。
const int N = _______;
int fac[N];//i!
int C(int n, int m)
{
return fac[n] / fac[n - m] / fac[m];
}
绝大多数组合数的计算结果都很大,所以题目中往往需要我们求组合数对一个大质数取模(例如 \(10^9+7\))的值,这时我们可以先预处理阶乘的逆元数组,通过乘法逆元求得组合数取模的值。
首先同样地,预处理一个阶乘数组 \(fac\)(注意,在此处 \(fac_n=n!\mod p\),其中 \(p\) 表示题干中给出的大质数)。
但是除法并不具有加法和乘法那样的模运算性质,即 \(\dfrac{a}{b}\mod p\neq \dfrac{a\mod p}{b\mod p}\),我们需要通过乘法逆元将除法转化为乘法。
预处理逆元数组 \(facinv\),计算公式为 \(facinv_n=(n!)^{-1}\mod p\)。此时有公式:
求逆元,由于 \(p\in P\),那么可以采用快速幂和费马小定理,时间复杂度为 \(O(n\log n)\)。
const int N = _______;
const int mod = _______;//p
int fac[N], facinv[N];
int qp(int a, int b)//quick_power: a^b mod p
{
int res = 1;
while(b)
{
if(b & 1) res = res * a % mod;
a = a * a % mod;
b >>= 1;
}
return res;
}
void init()//预处理fac[]与facinv[]
{
fac[0] = facinv[0] = 1;
for(int i = 1; i < N; i ++)
{
fac[i] = fac[i - 1] * i % mod;
facinv[i] = facinv[i - 1] * qp(i, mod - 2) % mod;
}
}
int C(int n, int m)
{
return fac[n] * facinv[n - m] % mod * facinv[m] % mod;
}
需要注意的是,预处理过程以及组合数的计算过程中的数字运算通常很巨大,因此最好提前将 int 类型替换为 long long 或 __int128 以避免溢出,本文为方便起见,统一采用 int。
Lucas 定理:
组合数的计算过程与上面一样,只是对于取模过程用到了 Lucas 定理(详见 Part1 数论):
int Lucas(int n, int m, int p)
{
if(m == 0) return 1;
return (C(n % p, m % p, p) * Lucas(n / p, m / p, p)) % p;
}
递推预处理组合数:
依据:\(\displaystyle \binom{n}{m}=\displaystyle \binom{n-1}{m}+\displaystyle \binom{n-1}{m-1}\)。
根据此递推式,我们可以通过两层循环预处理二维数组 \(C\),用于记录组合数的值,时间复杂度 \(O(n^2)\)。
const int N = _______, M = _______;
const int mod = _______;
int C[N][M];//C[i][j]: i选j
void init()
{
for(int i = 0; i < N; i ++)
for(int j = 0; j <= i; j ++)
if(j == 0) C[i][j] = 1;
else C[i][j] = (C[i - 1][j] + C[i - 1][j - 1]) % mod;
}
二项式定理与杨辉三角
二项式定理:
证明:当 \(n=1\) 时,原式显然成立。
假设当 \(n=m\) 时命题成立,当 \(n=m+1\) 时:
\(\displaystyle (a+b)^{m+1}=(a+b)(a+b)^m=(a+b)\sum^{m}_{i=0}\binom{m}{i}a^ib^{m-i}\)
\(\displaystyle =\sum^{m}_{i=0}\binom{m}{i}a^{i+1}b^{m-i}+\sum^{m}_{i=0}\binom{m}{i}a^ib^{m-i+1}=\sum^{m+1}_{i=1}\binom{m}{i-1}a^{i}b^{m-i+1}+\sum^{m}_{i=0}\binom{m}{i}a^ib^{m-i+1}\)
\(\displaystyle =\sum^{m+1}_{i=0}\left( \binom{m}{i-1}+\binom{m}{i} \right)a^ib^{m-i+1}=\sum^{m+1}_{i=0}\binom{m+1}{i}a^{i}b^{m+1-i}\)
由数学归纳法可知定理成立。
杨辉三角:
每行第一个数和最后一个数都为 \(1\),内部的数等于其左上角与右上角的两个数之和。这样递推定义所画出来的三角形被称为杨辉三角。

许多组合恒等式可以在杨辉三角图上形象地呈现出来,便于我们记忆。
排列组合中的计算技巧
推荐视频链接:link,讲的很仔细。
捆绑法:
设想这样一个问题,假设有编号为 \(1\to 5\) 的五个人要排成一排拍照,问排队方式有多少种。

在不加任何限制的前提下,我们很容易想到这是一个全排列问题,总的方案数就是 \(\text{A}^5_5=5!=120\)。
现在我们加上一条限制:由于 \(1\) 和 \(2\) 的关系很好,必须站在一起,问排队方式有多少种。此时我们仿佛不能直接求解了,加上这一限制后如果要用常规方式计算就很麻烦。
不妨考虑这样一个操作:既然 \(1\) 和 \(2\) 必须站在一起,那我们可以把他俩看成一个整体,把他俩“捆起来”,就像下图,此时我们就可以把 \(1\) 和 \(2\) 看作一个人。
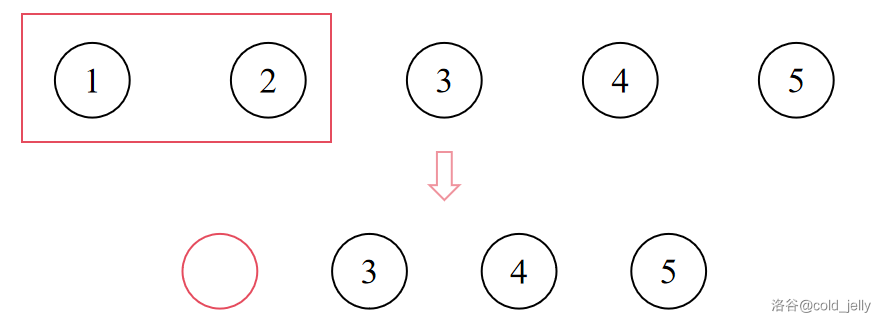
此时问题就转化为了 \(4\) 个人的全排列问题了,方案数为 \(\text{A}^4_4=4!=24\)。
注意,我们在一开始就将 \(1\) 和 \(2\) 绑了起来,现在还要给它们“松绑”,这时 \(1\) 和 \(2\) 之间也可以进行排列,所以还需要乘上 \(2\) 的全排列,即总方案数为 \(24\times 2!=48\)。
这种思想被称为捆绑法。
插空法:
还是举上面那个例子,\(5\) 个人排排站,但由于 \(3\) 和 \(4\) 有矛盾,不能站在一起,此时问总的排队方式有多少种。
我们可以有这样的考虑:\(3\) 和 \(4\) 他俩事儿多,把他俩踢出去,先把 \(1\)、\(2\)、\(5\) 给排了,就像这样:
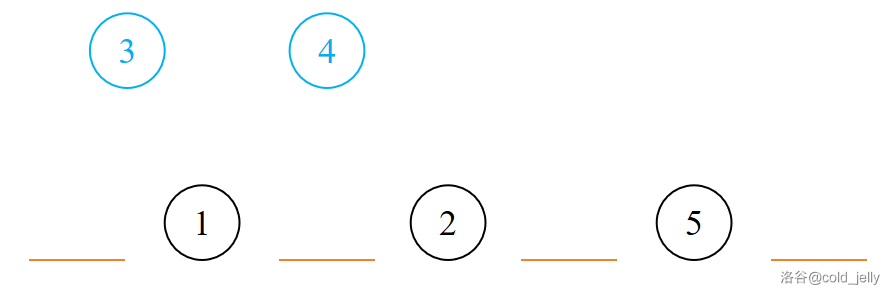
如图所示,在排好 \(1\)、\(2\)、\(5\) 之后,自动地就在 \(3\) 个人之间形成了 \(4\) 个空。我们要满足 \(3\) 和 \(4\) 不能站在一起,不就可以将他俩安置在这些空中吗?这种思想被称作插空法。此时相当于将 \(3\) 和 \(4\) 分置在两个不同的空中,方案数为 \(\displaystyle \text{A}^{2}_{4}=12\)。完了吗?我们在一开始就安排好了 \(1\)、\(2\)、\(5\),但是这三个人之间也有顺序之分呀,所以对于总方案数,根据乘法原理(分步),还需要乘上 \(3\) 的全排列,即总方案数为 \(12\times 3!=72\)。这是插空法的一大坑点,一定要格外注意。
隔板法:
(名额分配问题)假设现在有 \(10\) 个 NOIP 名额,要分配给 \(3\) 个竞赛班,要保证每个班至少分配 \(1\) 个名额,求分配方案数。
不妨假设这 \(10\) 个 NOIP 名额是 \(10\) 个没有差异的小球,现在我们要将其分为 \(3\) 堆,保证每堆至少有 \(1\) 个小球,问方案数。
由于这些小球之间没有差异,我们可以将其排为一排:

我们要将其划分为 \(3\) 组,不妨考虑就是用两个“隔板”(图中黄色线条)分割序列,我们要做的就是把这两个隔板插入 \(10\) 个小球之间的 \(9\) 个空中,总方案数就为 \(\displaystyle \binom{9}{2}=36\)。这种方法我们称作隔板法。
这题还有个变式:如果我们需要保证每个班至少分配 \(2\) 个名额呢?此时我们可以提前将 \(3\) 个名额分配给 \(3\) 个班,问题就转化为 \(7\) 个名额的问题了,通过类似的方法即可求解,总方案数为 \(\displaystyle \binom{7-1}{2}=15\)。
由此我们可以总结出一个公式:若名额有 \(n\) 个,要分为 \(k\) 组,且保证每组的名额至少为 \(a\),则总分配方式共有 \(\displaystyle \binom{n-k(a-1)}{k-1}=\binom{n-ka+k}{k-1}\) 种。
多重集的排列数与组合数
多重集是指包含重复元素的广义集合。设 \(S=\{n_1\times a_1,n_2\times a_2,...,n_k\times a_k\}\) 是由 \(n_1\) 个 \(a_1\),\(n_2\) 个 \(a_2\),...,\(n_k\) 个 \(a_k\) 组成的多重集,记 \(\displaystyle n=\sum^{k}_{i=1}n_i\),则 \(S\) 的全排列个数为:
这个数被称为多重集 \(S\) 的排列数。
设整数 \(r\leq n_i\)(\(\forall i\in [1,k]\))。从 \(S\) 中取出 \(r\) 个元素组成一个多重集(不考虑元素的顺序),根据隔板法可求出产生的不同多重集的数量为:
这个数被称为多重集 \(S\) 的组合数。
对于更一般的 \(r\),我们可使用容斥原理求出对应的多重集的组合数。
圆排列
直线排列与圆排列:
一般的排列数都是对于直线上的元素进行排列,我们把这种排列叫做直线排列。如图所示即为一个直线排列的例子。

而圆排列简单来说,就是排列的数围成了一个圆圈,如下图所示:
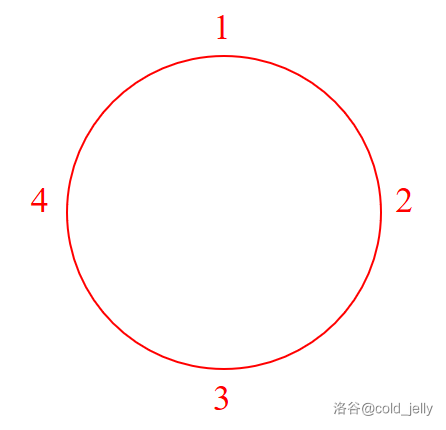
对于圆排列,也有类似于直线排列的排列数,叫做圆排列数,\(n\) 个数的全部圆排列数(即圆排列中的全排列)记作 \(\text{Q}^{n}_{n}\),部分圆排列数可记作 \(\text{Q}^{m}_{n}\)。
圆排列数的计算公式:
如何计算圆排列数呢?首先对于 \(n\) 个数直线排列,那么其排列数为 \(\text{A}^{n}_{n}\)。如果我们对于一个相同的圆排列通过断链做出不同的剖分,可以将其剖分成不同的直线排列:
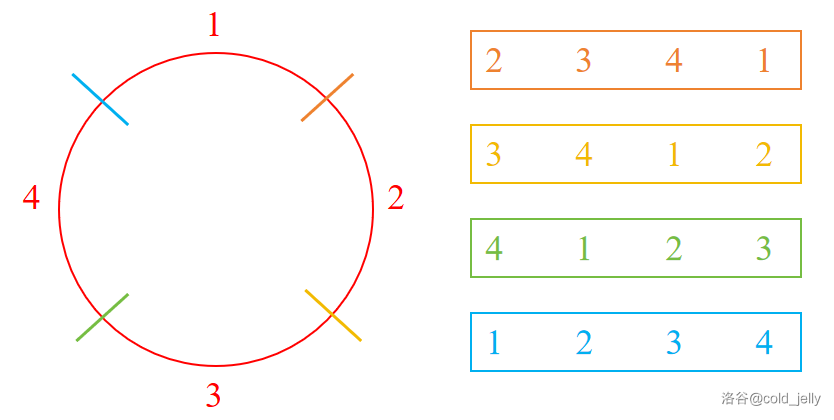
由图可知,对于 \(n\) 个数的圆排列,我们可以将其剖分为 \(n\) 种不同的直线排列,即这两个排列数之间有这样的关系:\(\text{A}^{n}_{n}=n\text{Q}^{n}_{n}\),因此我们可以推出全部圆排列数的计算公式:
类似地,我们可以推导出部分圆排列数的计算公式:
鸽巢原理
内容:将 \(n\) 个物品划分为 \(k\) 组,那么至少存在一组含有的物品数大于等于 \(\left \lceil \dfrac{n}{k} \right \rceil\)。
证明:考虑反证法。假设每组含有的物品数 \(n_i<\left \lceil \dfrac{n}{k} \right \rceil\),那么总数 \(\displaystyle \sum^{k}_{i=1}n_i\leq k\times \left( \left \lceil \dfrac{n}{k} \right \rceil -1 \right)=k\times \left \lceil \dfrac{n}{k} \right \rceil -k<k\left( \dfrac{n}{k}+1 \right) -k=n\),矛盾,故原命题得证。
鸽巢原理通常常被用于证明存在性和求最坏情况下的解。
容斥原理
集合中元素的个数:
对于一个集合 \(A\),我们用符号 \(\text{card}(A)\) 或 \(\left| A \right|\) 表示集合 \(A\) 中含有的元素个数。例如:\(\left| \{1,6,3,4\} \right|=4\)。本文统一采用后者。
容斥原理:
设 \(S_1,S_2,...,S_n\) 为有限集合,则有:
这就是容斥原理。
\(\mathbf{Venn}\) 图:
\(\text{Venn}\) 图:一种使用封闭平面几何图形和图形之间的交叉覆盖关系表示集合和集合之间的关系的集合表示法。
例子(用 \(\text{Venn}\) 图表示集合 \(A,B,C\)):
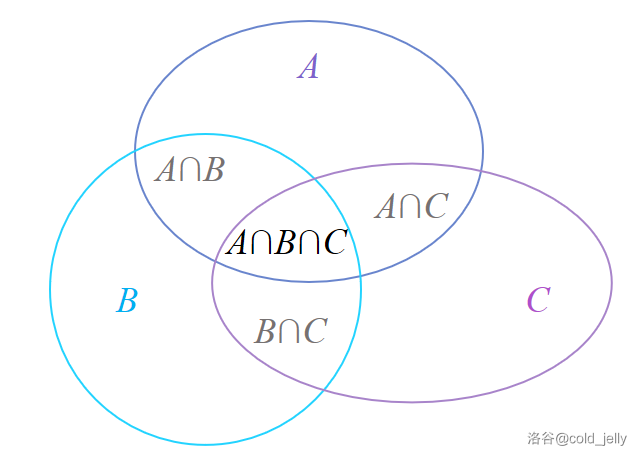
利用 \(\text{Venn}\) 图可以形象直观地表示抽象的集合概念。
补集:
对于全集 \(U\) 下集合的并可以采用容斥原理计算,而集合的交则用全集减去补集的并集得到:
对右边使用容斥原理即可。其中符号 \(\overline{A}\) 表示集合 \(A\) 在给定的全集 \(U\) 意义下的补集,等价于 \(\complement_U A\),本文统一采用前者。
错位排列
定义:错位排列是指没有任何元素出现在其有序位置的排列。即对于一个 \(1\to n\) 的排列 \(P\),如果满足 \(\forall i\in [1,n],P_i\neq i\),则称 \(P\) 是 \(n\) 的一个错位排列。
例如,\(\{2,3,1\}\) 和 \(\{3,1,2\}\) 是当 \(n=3\) 时的错位排列。
错位排列数及其通项公式:
\(n\) 所对应的错位排列的总数叫做错位排列数,记作 \(D_n\),例如 \(D_3=2\)。
如何计算 \(D_n\) 呢?利用容斥原理,不妨设全集 \(U\) 表示不加限制时总的排列数,即 \(|U|=n!\)。套用上文的补集公式可知我们要求的答案为 \(\displaystyle |U|-\left| \bigcup^{n}_{i=1}\overline{S_i} \right|\)。其中,\(\overline{S_i}\) 的含义是满足 \(P_i=i\) 的排列的数量。用容斥原理把式子展开,需要对若干个特定的集合的交集求大小,即求 \(\displaystyle \sum_{a_i<a_{i+1}}\left| \bigcap^{m}_{i=1}S_{a_i} \right|\)。上述 \(k\) 个集合的交集表示有 \(k\) 个变量满足 \(P_{a_i}=a_i\) 的排列数,而剩下 \(n-k\) 个数的位置任意,因此有:
选择 \(k\) 个元素的方案数为 \(\displaystyle \binom{n}{k}\),因此有:
所以有:
这就是错位排列数的通项公式。
递推计算错位排列数:
直接使用通项公式计算对计算机显然是不友好的,我们还可以采用递推的方式计算错位排列数。
考虑这样一个问题,现在有 \(n\) 个元素进行错位排列,要使其形成错位排列,在排 \(n\) 时考虑两种递推:
- 前 \(n-1\) 个元素全部排错;
- 前 \(n-1\) 个元素有一个没错其余全错。
对于第一种情况,因为前 \(n-1\) 个元素全部排错,因此在排 \(n\) 时只需要将其与前面的任一元素交换位置即可得到新的错位排列,总方案数为 \(D_{n-1}\times (n-1)\)。
对于第二种情况,前面 \(n-1\) 个元素有一个没有错位其余全部错位:考虑这种情况的目的在于,若 \(n-1\) 个元素中如果有一个没错位,那么把那个没错的与 \(n\) 交换,即可得到一个错位排列。
对于其他情况,不能在一次操作内将其变为一个错位排列。
于是错位排列数满足递推关系:
可以用代码在 \(O(N)\) 时间复杂度内在给定的上界 \(N\) 范围内求得所有数的错位排列数。
递推代码:
const int N = _______;
int D[N];//错位排列数
void init()
{
D[1] = 0, D[2] = 1;//边界
for(int i = 3; i < N; i ++)
D[i] = (i - 1) * (D[i - 1] + D[i - 2]);
}
使用递归也可在线询问错位排列数,时间复杂度为 \(O(n)\)。代码:
int D(int n)//错位排列数
{
if(n == 1) return 0;//边界
if(n == 2) return 1;//边界
return (n - 1) * (D(n - 1) + D(n - 2));
}
卡特兰数
卡特兰数列的通项公式:
对于卡特兰数 \(H_n\)(\(n\geq 1\)),有公式:
这是卡特兰数列的通项公式。
利用代码实现求卡特兰数,时间复杂度与求组合数的时间复杂度一致:
int H(int n)//卡特兰数
{
return C(2 * n, n) / (n + 1);
}
与卡特兰数相关问题:
- \(n\) 个左括号和 \(n\) 个右括号组成的合法括号序列数为 \(H_n\);
- 编号 \(1\to n\) 的 \(n\) 个数经过一个栈,形成的合法出栈序列数为 \(H_n\);
- \(n\) 个不同节点构成的不同二叉树的数量为 \(H_n\);
- 在平面直角坐标系中,每一步只能向上或向右走,从 \((0,0)\) 走到 \((n,n)\) 并且除端点外不接触直线 \(f(x)=x\) 的合法路线数量为 \(2H_{n-1}\)。
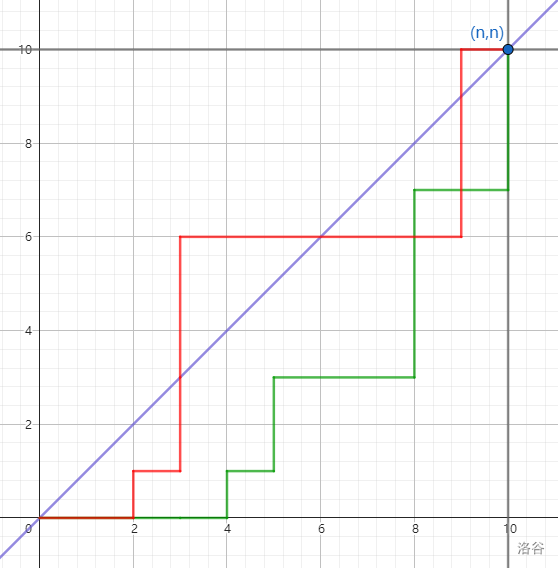
求卡特兰数的常用公式:
- \(H_n=\dfrac{H_{n-1}(4n-2)}{n+1}\),时间复杂度 \(O(N)\):
const int N = _______;
int H[N];//卡特兰数
void init()
{
H[1] = 1;//边界
for(int i = 2; i < N; i ++)
H[i] = H[i - 1] * (4 * i - 2) / (n + 1);
}
- \(\displaystyle H_n=\binom{2n}{n}-\binom{2n}{n-1}\),时间复杂度与求组合数的时间复杂度一致:
int H(int n)//卡特兰数
{
return C(2 * n, n) - C(2 * n, n - 1);
}
第二类斯特林数
定义:将 \(n\) 个两两不同的元素划分为 \(m\) 个互不区分的非空子集的方案数为 \(\begin{Bmatrix} n \\ m \end{Bmatrix}\),这个数叫做第二类斯特林数。
递推式:
边界是 \(\begin{Bmatrix} n \\ 0 \end{Bmatrix}=[n=0]\),其中 \([P]\) 为艾佛森括号,当命题 \(P\) 为真时 \([P]=1\),否则 \([P]=0\)。
通项公式:
二项式反演
反演:
对于两个数列 \(g(x)\),\(f(x)\) 而言,若它们之间存在某种对应关系,使得不仅能从 \(f(x)\) 推出 \(g(x)\),还能从 \(g(x)\) 反推出 \(f(x)\),那么这个反推的过程就叫做反演。
在一些特殊的对应关系中,反演会化出一些优美的形式,例如莫比乌斯反演,单位根反演,子集反演,二项式反演等。
二项式反演:
记 \(f(n)\) 表示恰好使用 \(n\) 个不同元素形成特定结构的方案数,\(g(n)\) 表示从 \(n\) 个不同元素中选出 \(i\ge 0\) 个元素形成特定结构的总方案数。
若已知 \(f(n)\) 求 \(g(n)\),那么有:
若已知 \(g(n)\) 求 \(f(n)\),那么有:
上述已知 \(g(n)\) 求 \(f(n)\) 的过程就被称为二项式反演。
证明:
将反演公式的 \(g(i)\) 展开得到:
先枚举 \(j\),再枚举 \(i\),得到:
使用公式 \(\displaystyle \binom{n}{r}\binom{r}{k}=\binom{n}{k}\binom{n-k}{r-k}\) 得到:
令 \(k=i-j\)。则 \(i=k+j\),上式转换为:
使用公式 \(\displaystyle \sum^{n}_{i=0}(-1)^i\binom{n}{i}=[n=0]\) 得到:
证毕。
Part4 线性代数
向量的概念与基本运算
向量的有关概念:
定义:既有大小又有方向的量叫做向量,记作 \(\boldsymbol{a}\)。在不改变向量的大小和方向下,可以将其任意平移。
有向线段:带有方向的线段,线段 \(AB\) 对应的有向线段记作 \(\overrightarrow{AB}\),它还反映了该有向线段的起点为 \(A\),终点为 \(B\)。我们通常使用有向线段来形象表示向量。
向量的模:有向线段 \(\overrightarrow{AB}\) 的长度被称为该向量的模,记作 \(\left| \overrightarrow{AB} \right|\)。
零向量:模为 \(0\) 的向量,记作 \(\boldsymbol{0}\)。零向量的方向任意。
单位向量:模为 \(1\) 的向量被称为该方向上的单位向量,记作 \(\boldsymbol{e}\)。
平行向量:方向相同或相反的两个非零向量叫做平行向量,记作 \(\boldsymbol{a}\parallel \boldsymbol{b}\)。平行向量又叫共线向量。
相等向量与相反向量:方向相同且模相等的两个向量叫做相等向量;方向相反且模相等的两个向量叫做相反向量。
向量的夹角:已知两非零向量 \(\boldsymbol{a}\) 和 \(\boldsymbol{b}\),记 \(\theta=\left \langle \boldsymbol{a},\boldsymbol{b} \right \rangle\) 表示它们的夹角大小,并规定 \(\theta\in [0,\pi]\)。当 \(\theta=0\) 时,两向量同向;当 \(\theta=\pi\) 时,两向量反向;当 \(\theta=\dfrac{\pi}{2}\) 时,两向量垂直,记作 \(\boldsymbol{a}\perp \boldsymbol{b}\)。
向量的加减:
向量的加减法可以类比物理学中的位移理解:
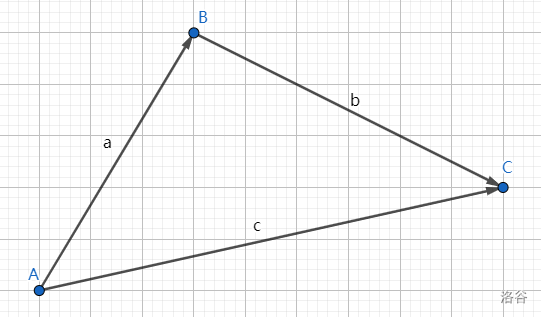
在上图中,有结论 \(\boldsymbol{a}+\boldsymbol{b}=\boldsymbol{c}\),这叫做三角形法则。
我们可以假设人在 \(A\) 地,要前往 \(C\) 地,那么无论他途径 \(B\) 地还是径直走向 \(C\) 地,达成的效果是一致的,所以这两种方式在向量意义下等价,故 \(\boldsymbol{a}+\boldsymbol{b}=\boldsymbol{c}\)。该式经过移项也可变为:\(\boldsymbol{b}=\boldsymbol{c}-\boldsymbol{a}\)。
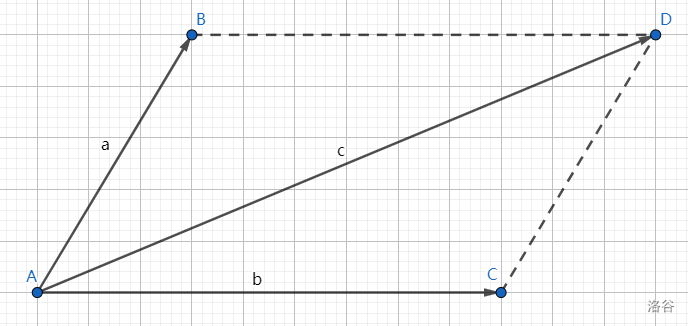
在上图中,向量 \(\boldsymbol{a},\boldsymbol{b},\boldsymbol{c}\) 恰组成平行四边形,此时由于向量可自由平移,故上图可等价变为三角形图,进而得到 \(\boldsymbol{a}+\boldsymbol{b}=\boldsymbol{c}\),这叫做平行四边形法则。
对于首尾相连的向量,还有一种快捷的计算方式:
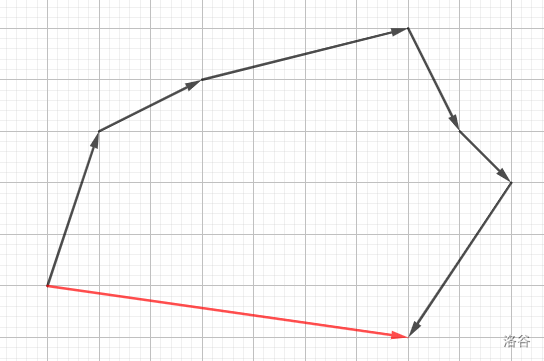
与三角形法则类似地,上图中所有黑色向量之和等于红色向量。
向量的数乘:
向量的数乘在几何意义上表现为向量的伸缩。

如图所示,当一个向量 \(\boldsymbol{a}\) 乘上一个实数 \(\lambda\) 时,其模长 \(\left| \boldsymbol{a}\right| \to \left| \lambda \boldsymbol{a}\right| =|\lambda| \left| \boldsymbol{a} \right|\);当 \(\lambda>0\) 时同向,当 \(\lambda=0\) 时 \(\lambda \boldsymbol{a}=\boldsymbol{0}\),当 \(\lambda<0\) 时反向。
向量的数乘有如下运算律:
- \(\lambda\left(\mu \boldsymbol{a}\right)=(\lambda\mu)\boldsymbol{a}\);
- \((\lambda+\mu)\boldsymbol{a}=\lambda \boldsymbol{a}+\mu \boldsymbol{a}\);
- \(\lambda\left(\boldsymbol{a}+\boldsymbol{b}\right)=\lambda \boldsymbol{a}+\lambda \boldsymbol{b}\)。
向量的加减与数乘统称为向量的线性运算。
平面向量基本定理及其坐标表示
平面向量基本定理:
内容:如果两向量 \(\boldsymbol{e_1},\boldsymbol{e_2}\) 不共线,那么存在唯一实数对 \((x,y)\) 使得与 \(\boldsymbol{e_1},\boldsymbol{e_2}\) 共面的向量 \(\boldsymbol{p}\) 满足 \(\boldsymbol{p}=x\boldsymbol{e_1}+y\boldsymbol{e_2}\)。
根据平行四边形法则的逆定理,我们可以将一个向量用两个不共线的向量任意分解:
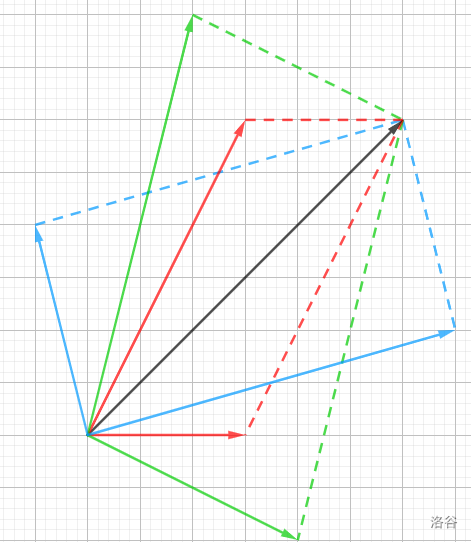
在同一平面内的不共线的两个向量称为基底,如果基底互相垂直,那么就是对一个向量正交分解。
平面向量的坐标表示与线性运算:
如果取与横轴与纵轴方向相同的单位向量 \(i,j\) 作为一组基底,根据平面向量基本定理,平面上的所有向量与有序实数对 \((x,y)\) 一一对应。
而有序实数对 \((x,y)\) 与平面直角坐标系上的点一一对应,于是作向量 \(\overrightarrow{OP}=\boldsymbol{p}\)(起点为原点 \(O\)),那么终点 \(P(x,y)\) 也是唯一确定的。由于研究的对象是自由向量,可以自由平移起点,这样,在平面直角坐标系里,每一个向量都可以用有序实数对唯一表示。
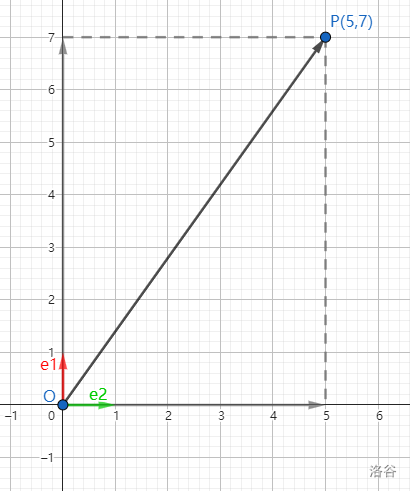
对于两个向量 \(\boldsymbol{a}=(x_1,y_1),\boldsymbol{b}=(x_2,y_2)\),它们的线性运算可以这样定义:
- \(\boldsymbol{a}\pm \boldsymbol{b}=(x_1\pm x_2,y_1\pm y_2)\);
- \(\lambda \boldsymbol{a}=(\lambda x_1,\lambda y_1)\)。
设平面中两点 \(A(a,b),B(c,d)\),则 \(\overrightarrow{AB}=(c-a,d-b)\)。
矩阵及其运算
矩阵:
一个 \(n\times m\) 的矩阵 \(A\) 可以看作一个 \(n\times m\) 的二维数组。即:
特别地,当 \(n=m\) 时,该矩阵被称为 \(n\) 阶方阵。
矩阵的线性运算:
矩阵的加减与数乘合称矩阵的线性运算。其运算与向量的线性运算类似:
矩阵的转置:
矩阵的转置,就是把矩阵的行与列互换。矩阵 \(A\) 经过转置后得到的矩阵记作 \(A^T\),例如:
矩阵的转置满足以下运算律:
- \((A^T)^T=A\);
- \((\lambda A)^T=\lambda A^T\);
- \((AB)^T=B^TA^T\)。
矩阵乘法:
设 \(A\) 是 \(n\times m\) 矩阵,\(B\) 是 \(m\times p\) 矩阵,则 \(C=A\times B\) 是 \(n\times p\) 矩阵,并且有:
例如:
矩阵乘法满足以下运算律:
- \((AB)C=A(BC)\);
- \((A+B)C=AC+BC\);
- \(C(A+B)=CA+CB\);
矩阵乘法不满足交换律。
利用矩阵乘法的结合律,计算矩阵乘法的过程可用快速幂来优化。
分析:题意很简单,给定 \(n\times n\) 的矩阵 \(A\),求 \(A^k\)。\(n\leq 100\),\(k\leq 10^12\)。
与快速幂类似原理,将其改为矩阵乘法形式,重载一下运算符就行了。
代码如下:
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N = 110, mod = 1e9 + 7;
struct matrix//矩阵
{
int S[N][N];//N * N矩阵
};
matrix Base;//原矩阵
matrix Ans;//答案
int n, k;
matrix operator *(const matrix &A, const matrix &B)//重载*运算符
{
matrix C;//A * B = C
for(int i = 1; i <= n; i ++)
for(int j = 1; j <= n; j ++)
C.S[i][j] = 0;
for(int i = 1; i <= n; i ++)
for(int j = 1; j <= n; j ++)
for(int k = 1; k <= n; k ++)
{
C.S[i][j] += A.S[i][k] * B.S[k][j] % mod;
C.S[i][j] %= mod;
}
return C;
}
void init()//预处理答案矩阵对角线
{
for(int i = 1; i <= n; i ++)
Ans.S[i][i] = 1;
}
void qp()//矩阵快速幂
{
while(k)
{
if(k & 1) Ans = Ans * Base;
Base = Base * Base;
k >>= 1;
}
}
signed main()
{
cin >> n >> k;
init();
for(int i = 1; i <= n; i ++)
for(int j = 1; j <= n; j ++)
scanf("%lld", &Base.S[i][j]);
qp();
for(int i = 1; i <= n; i ++)
{
for(int j = 1; j <= n; j ++)
printf("%lld ", Ans.S[i][j]);
puts("");
}
return 0;
}
矩阵乘法的代码实现通常有两种,一种为重载运算符,另一种直接在外部函数动态修改。在本题中我们采取了前者,在下一道例题中我们将采用后者。
矩阵乘法加速递推:
例题:P1962 斐波那契数列
分析:直接递推计算,时间复杂度为 \(O(n)\),不过 \(Fib(n)\) 的值只与 \(Fib(n-1)\) 和 \(Fib(n-2)\) 有关,我们在递推时只需要保存最近的两个斐波那契数即可得到下一个斐波那契数。
设矩阵 \(F(n)=\begin{bmatrix} Fib(n) & Fib(n+1)\end{bmatrix}\)。
此时有递推公式:\(\begin{bmatrix} Fib(n) & Fib(n+1)\end{bmatrix}=\begin{bmatrix} Fib(n-1) & Fib(n)\end{bmatrix}\times \begin{bmatrix} 0 & 1\\ 1 & 1 \end{bmatrix}\)。
我们可以采用矩阵乘法加速递推,时间复杂度为 \(O(2^3\log n)\)。
代码如下:
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int mod = 1e9 + 7;
int n;
void mul(int f[2], int a[2][2])
{
int c[2];
memset(c, 0, sizeof c);
for(int i = 0; i < 2; i ++)
for(int j = 0; j < 2; j ++)
c[i] = (c[i] + f[j] * a[j][i]) % mod;
memcpy(f, c, sizeof c);
}
void mulself(int a[2][2])//自乘
{
int c[2][2];
memset(c, 0, sizeof c);
for(int i = 0; i < 2; i ++)
for(int j = 0; j < 2; j ++)
for(int k = 0; k < 2; k ++)
c[i][j] = (c[i][j] + a[i][k] * a[k][j]) % mod;
memcpy(a, c, sizeof c);
}
void qp()//快速幂
{
while(n)
{
if(n & 1) mul(f, a);
mulself(a);
n >>= 1;
}
}
signed main()
{
cin >> n;
int f[2] = {0, 1};
int a[2][2] = {{0, 1}, {1, 1}};
qp();
cout << f[0];
return 0;
}
一般来说,如果一类问题具有以下特点:
- 可以抽象为一个长度为 \(n\) 的一维向量,该向量在每个单位时间发生一次变化;
- 变化的形式是一个线性递推;
- 该递推式在每一个单位时间内可能作用于不同的数据上,但本身保持不变;
- 向量变化时间(递推轮数)很长,但 \(n\) 不大。
那么可以考虑使用矩阵乘法加速递推。我们把该一维向量叫做“状态矩阵”,把用于与“状态矩阵”相乘的本身不变的矩阵称为“转移矩阵”。若状态矩阵中的第 \(x\) 个数对下一单位时间中的第 \(y\) 个数产生影响,则把转移矩阵的第 \(x\) 行第 \(y\) 列赋值为适当的系数。
若递推总轮数为 \(T\),则时间复杂度为 \(O(n^3\log T)\)。
特殊矩阵
三角矩阵:如果方阵主对角线左下方的元素均为 \(0\),称为上三角矩阵。如果方阵主对角线右上方的元素均为 \(0\),称为下三角矩阵。
两个上(下)三角矩阵的乘积仍然是上(下)三角矩阵。如果对角线元素均非 \(0\),则上(下)三角矩阵可逆,逆也是上(下)三角矩阵。
对称矩阵:若 \(n\times m\) 矩阵 \(A\) 满足 \(\forall i\in [1,n],\forall j\in [1,m]\),\(A_{i,j}=A_{j,i}\),则 \(A\) 为对称矩阵。
单位矩阵:主对角线上的元素为 \(1\),其余为 \(0\)。一般记作 \(I\)。
稀疏矩阵与稠密矩阵:在矩阵中,若数值为 \(0\) 的元素数目远远多于非 \(0\) 元素的数目,并且非 \(0\) 元素分布没有规律时,则称该矩阵为稀疏矩阵;与之相反,若非 \(0\) 元素数目占大多数时,则称该矩阵为稠密矩阵。
高斯消元算法
矩阵的初等变换:
矩阵的初等行变换和初等列变换合称矩阵的初等变换,变换前后的矩阵等价。
矩阵的初等行变换有三种:
- 倍乘:用一个非 \(0\) 数乘以某一行。例如:\(\begin{bmatrix} 3 & 2\\ 4 & 1\\ 6 & 3 \end{bmatrix}\Longleftrightarrow \begin{bmatrix} 3\times 15 & 2\times 15\\ 4 & 1\\ 6 & 3 \end{bmatrix}\);
- 对换:将矩阵的两行交换位置。例如:\(\begin{bmatrix} 3 & 2\\ 4 & 1\\ 6 & 3 \end{bmatrix}\Longleftrightarrow \begin{bmatrix} 4 & 1\\ 3 & 2\\ 6 & 3 \end{bmatrix}\);
- 倍加:把矩阵的一行的若干倍加到另一行。例如:\(\begin{bmatrix} 3 & 2\\ 4 & 1\\ 6 & 3 \end{bmatrix}\Longleftrightarrow \begin{bmatrix} 3 & 2\\ 4 & 1\\ 6+4\times 15 & 3+1\times 15 \end{bmatrix}\)。
把上述操作的行改为列,就是矩阵的初等列变换了。
高斯消元算法:
高斯消元是一种求解线性方程组的方法。所谓线性方程组,是由 \(m\) 个 \(n\) 元一次方程构成的。线性方程组的所有系数加上等号后的常数可以写成一个 \(m\) 行 \(n+1\) 列的增广矩阵。例如:
通过若干次初等行变换后可以将上面的矩阵变为 \(\begin{bmatrix} 1 & 2 & -1 & -6\\ 0 & 1 & 1 & 1\\ 0 & 0 & 1 & 3 \end{bmatrix}\),得到了一个系数矩阵部分为上三角矩阵的矩阵。
该矩阵表示为方程组形式为:\(\left\{\begin{matrix} x_1+2x_2-x_3=-6 \\ x_2+x_3=1 \\ x_3=3 \end{matrix}\right.\)。
该矩阵也可以进一步化简为 \(\begin{bmatrix} 1 & 0 & 0 & 1\\ 0 & 1 & 0 & -2\\ 0 & 0 & 1 & 3 \end{bmatrix}\),此时该矩阵被称为“简化阶梯形矩阵”,它直接给出了方程组的解。这种通过初等行变换把增广矩阵化为简化阶梯形矩阵的线性方程组求解算法就是高斯消元算法(高斯-约旦消元算法)。
高斯消元算法的思想就是对于每一个未知量 \(x_i\),找到一个 \(x_i\) 的系数非 \(0\)。但 \(x_1\to x_{i-1}\) 的系数都是 \(0\) 的方程,通过初等行变换把其他方程的 \(x_i\) 的系数全部化为 \(0\)。
在高斯消元的过程中,可能会遇到一些特殊情形,需要我们分类讨论。
在高斯消元完成后,若存在系数全为 \(0\)、常数不为 \(0\) 的行,则方程组无解。若系数不全为 \(0\) 的行恰好有 \(n\) 个,则说明方程有唯一解。若系数不全为 \(0\) 的行小于 \(n\) 个,则方程组有无数组解。
代码如下:
#include<bits/stdc++.h>
using namespace std;
const int N = 110;
const double eps = 1e-7;//精确度
int n;
double sq[N][N];//方程组
double ans[N];//答案
int main()
{
cin >> n;
for(int i = 1; i <= n; i ++)
for(int j = 1; j <= n + 1; j ++)
cin >> sq[i][j];
for(int i = 1; i <= n; i ++)
{
int r = i;
for(int j = i + 1; j <= n; j ++)
if(fabs(sq[r][i]) < fabs(sq[j][i])) r = j;
if(fabs(sq[r][i]) < eps) return puts("No Solution"), 0;//无解
if(i != r) swap(sq[i], sq[r]);
double q = sq[i][i];
for(int j = i; j <= n + 1; j ++)
sq[i][j] /= q;
for(int j = i + 1; j <= n; j ++)
{
q = sq[j][i];
for(int k = i; k <= n + 1; k ++)
sq[j][k] -= sq[i][k] * q;
}
}
ans[n] = sq[n][n + 1];
for(int i = n - 1; i >= 1; i --)//回带
{
ans[i] = sq[i][n + 1];
for(int j = i + 1; j <= n; j ++)
ans[i] -= (sq[i][j] * ans[j]);
}
for(int i = 1; i <= n; i ++) printf("%.2lf\n", ans[i]);
return 0;
}
线性空间
线性空间是一个关于以下两个运算封闭的向量集合。
- 向量加法 \(\boldsymbol{a}+\boldsymbol{b}\);
- 数乘 \(\lambda \boldsymbol{a}\)。
给定若干个向量 \(\boldsymbol{a_1},\boldsymbol{a_2},...,\boldsymbol{a_k}\),若向量 \(\boldsymbol{b}\) 能由 \(\boldsymbol{a_1},\boldsymbol{a_2},...,\boldsymbol{a_k}\) 经过向量加法和数乘运算得出,则称向量 \(\boldsymbol{b}\) 能被 \(\boldsymbol{a_1},\boldsymbol{a_2},...,\boldsymbol{a_k}\) 表出。\(\boldsymbol{a_1},\boldsymbol{a_2},...,\boldsymbol{a_k}\) 能表出的所有向量构成一个线性空间,\(\boldsymbol{a_1},\boldsymbol{a_2},...,\boldsymbol{a_k}\) 被称为这个线性空间的生成子集。
任意选出线性空间内的若干个向量,如果其中存在一个向量能被其他向量表出,则称这些向量线性相关,否则称他们线性无关。
线性相关的生成子集被称为线性空间的基底,简称基。一个线性空间的所有基包含的向量个数都相等,这个数被称为线性空间的维数。
对于一个 \(n\times m\) 的矩阵,我们可以把它的每一行看作一个长度为 \(m\) 的向量,称为行向量。矩阵的 \(n\) 个行向量能够表出的所有向量构成一个线性空间,其维数被称为矩阵的行秩。类似地,我们可定义矩阵的列向量与列秩。实际上矩阵的行秩一定等于列秩,它们被称为矩阵的秩。
线性基
定义:称线性空间 \(V\) 的一个极大线性无关组为 \(V\) 的一组线性基。
线性基的势:我们定义线性空间 \(V\) 的维数为线性基的势,记作 \(\dim(V)\)。
线性基的部分性质:
对于有限维线性空间 \(V\), 设其维数为 \(n\), 则:
- \(V\) 中的任意 \(n+1\) 个向量线性相关;
- \(V\) 中的任意 \(n\) 个线性无关的向量均为 \(V\) 的基;
- 若 \(V\) 中的任意向量均可被向量组 \(\boldsymbol{a_1},\boldsymbol{a_2},...,\boldsymbol{a_n}\) 线性表出,则其是 \(V\) 的一个基;
- \(V\) 中任意线性无关向量组 \(\boldsymbol{a_1},\boldsymbol{a_2},...,\boldsymbol{a_m}\) 均可通过插入一些向量使得其变为 \(V\) 的一个基。
Part5 概率论
基本概念
样本空间:样本空间 \(\Omega\),指明随机现象所有可能出现的结果。
事件域:事件域 \(\mathcal{F}\),表示我们所关心的所有事件构成的集合。
概率:事件发生的可能性,记作 \(P\)。
随机事件:
一个随机现象中可能发生的不能再细分的结果被称为样本点。所有样本点的集合称为样本空间。而一个随机事件是样本空间的一个子集,其由若干个样本点构成。
对于一个随机现象的结果 \(\omega\) 和一个随机事件 \(A\),我们称事件 \(A\) 发生了当且仅当 \(\omega\in A\)。
事件的运算:
事件本质上就是一个集合,事件之间的运算就是集合的运算。
和事件:事件的并 \(A\cup B\) 可记作 \(A+B\),被称为和事件。
积事件:事件的交 \(A\cap B\) 可记作 \(AB\),被称为积事件。
事件域的性质:
事件域 \(\mathcal{F}\) 对在补运算、可数并、可数交下是封闭的,且包含元素 \(\varnothing\)。
即:
- \(\varnothing\in \mathcal{F}\);
- 若 \(A \in \mathcal{F}\),则 \(\bar{A}\in \mathcal{F}\);
- 若 \(A_{1\to n}\in \mathcal{F}\),则 \(\displaystyle \bigcup^{n}_{i=1}A_i\in \mathcal{F}\)。
概率空间:
我们把三元组 \((\Omega,\mathcal{F},P)\) 称为概率空间。
概率的定义
古典定义:
对于事件 \(A\),其在事件域 \(\mathcal{F}\)(即所有可能的事件构成的集合)中发生的概率 \(P(A)\) 被定义为:
其中 \(\#(A)\) 表示集合 \(A\) 的相对大小度量。
公理化定义:
设样本空间为 \(\Omega\),若 \(\forall A\subseteq \Omega\),存在实值函数 \(P(A)\) 满足:
- \(P(A)\geq 0\);
- \(P(\Omega)=1\);
- 对于若干两两互斥事件 \(A_1,A_2,...\),有 \(\displaystyle \sum P(A_i)=P\left(\bigcup A_i\right)\)。
则称 \(P(A)\) 为随机事件 \(A\) 发生的概率。
条件概率
定义:若已知事件 \(A\) 发生,在此条件下事件 \(B\) 发生的概率称为条件概率,记作 \(P(B|A)\)。
在概率空间 \((\Omega,\mathcal{F},P)\) 中,若事件 \(A\in \mathcal{F}\) 满足 \(P(A)>0\),则 \(\forall B\in \mathcal{F}\) 有公式:
此时 \(P(B|A)\) 是 \((\Omega,\mathcal{F})\) 上的概率函数。
由条件概率的定义公式可以直接导出以下两个公式:
概率乘法公式:在概率空间 \((\Omega,\mathcal{F},P)\) 中,若 \(P(A)>0\),则 \(\forall B\in \mathcal{F}\),
\[\boxed{P(AB)=P(A)P(B|A)} \]
全概率公式:在概率空间 \((\Omega,\mathcal{F},P)\) 中,若一组事件 \(A_1,A_2,...,A_n\) 两两不交且 \(\displaystyle \bigcup^{n}_{i=1}A_i=\Omega\),则 \(\forall B\in \mathcal{F}\),
\[\displaystyle \boxed{P(B)=\sum^{n}_{i=1}P(A_i)P(B|A_i)} \]
贝叶斯公式:
导致事件 \(B\) 发生的原因为 \(A_1,A_2,...,A_n\),则在已知 \(P(A_i)\) 和 \(P(B|A_i)\) 时可以通过全概率公式计算 \(P(B)\),但很多情况下我们需要通过“事件 \(B\) 发生”这一条件反推各个原因事件的发生概率。这时有公式:
这就是贝叶斯公式。
事件之间的关系
事件的独立性:
定义:对于同一概率空间内的事件 \(A,B\),若 \(P(AB)=P(A)P(B)\),则称 \(A,B\) 独立。
对于两个相互独立的事件 \(A,B\),有 \(P(A|B)=P(A)\) 和 \(P(B|A)=P(B)\)。即事件 \(A\) 与事件 \(B\) 发生的概率不受对方发生的概率影响。
多个事件的独立性:
类比两个事件的独立性定义,我们可以定义出多个事件的独立性。
对于多个事件 \(A_1,A_2,...,A_n\),我们称其独立,当且仅当对任意一组事件 \(\{A_{i_k}| 1 \leq i_1 < i_2 < ... < i_k \leq n \}\) 都有 \(\displaystyle P(A_{i_1}A_{i_2}\cdots A_{i_r})=\prod^{r}_{j=1}P(A_{i_j})\)。
事件的互斥性:
定义:对于同一概率空间内的事件 \(A,B\),若 \(P(AB)=0\) 且 \(P(A),P(B)\neq 0\),则称事件 \(A,B\) 是互斥的。
若事件 \(A,B\) 互斥,则有 \(P(A|B)=P(B|A)=0\)。也就是说,因为 \(A,B\) 互斥,所以在对方发生的情况下,该事件不能再发生,故条件概率为 \(0\)。
随机变量
定义:给定概率空间 \((\Omega,\mathcal{F},P)\),定义在 \(\Omega\) 上的函数 \(X:\Omega\to \mathbf{R}\) 若满足 \(\forall t\in \mathbf{R}\),都有 \(\{\omega\in \Omega|X(\omega)\leq t\}\in \mathcal{F}\),则称 \(X\) 为随机变量。
示性函数与分布函数:
示性函数:对于 \(A\subseteq \Omega\),定义随机变量 \(I_A(\omega)=\left\{\begin{matrix} 1 & \omega\in A\\ 0 & \omega\notin A\end{matrix}\right.\) 为事件 \(A\) 的示性函数。
分布函数:对于随机变量 \(X\),称函数 \(F(x)=P(X\leq x)\) 为随机变量 \(X\) 的分布函数,记作 \(X\sim F(x)\)。
分布函数具有以下性质:
- 右连续性:\(F(x)=F(x+0^+)\),即分布函数是连续的;
- 单调性:\(F(x)\) 在 \(\mathbf{R}\) 上单调递增(非严格);
- \(\displaystyle \lim_{x\to -∞}F(x)=0\),\(\displaystyle \lim_{x\to +∞}F(x)=1\)。
离散型随机变量:
若一个随机变量的值域可数,则称该随机变量是离散的,叫做离散型随机变量。对应地,我们也可定义连续型随机变量,我们主要讨论离散型随机变量。
设离散型随机变量 \(X\),其所有可能的取值为 \(x_1,x_2,...,x_n\),我们可以用一系列形如 \(P(X=x_i)=p_i\) 的等式或下表表示:
| \(X\) | \(x_1\) | \(x_2\) | \(...\) | \(x_n\) |
|---|---|---|---|---|
| \(P\) | \(p_1\) | \(p_2\) | \(...\) | \(p_n\) |
这就是离散型随机变量的分布列。
随机变量的独立性:若随机变量 \(X,Y\) 满足 \(\forall x,y\in \mathbf{R}\),\(P(X\leq x,Y\leq y)=P(X\leq x)P(Y\leq y)\),则称随机变量 \(X,Y\) 独立。
随机变量的数字特征
数学期望及其性质:
若离散型随机变量的分布列为:
| \(X\) | \(x_1\) | \(x_2\) | \(...\) | \(x_n\) |
|---|---|---|---|---|
| \(P\) | \(p_1\) | \(p_2\) | \(...\) | \(p_n\) |
则称
为 \(X\) 的数学期望,简称期望。
期望具有如下性质:
- 线性性:\(E(aX\pm bY)=aE(X)\pm bE(Y)\);
- 积性:若随机变量 \(X,Y\) 的期望存在且 \(X,Y\) 相互独立,则有 \(E(XY)=E(X)E(Y)\)。
期望与概率可以通过示性函数 \(I_A\) 转化:
条件分布与条件期望:
定义:对于两个随机变量 \(X,Y\),在已知 \(Y=y\) 的条件下 \(X\) 的概率分布称之为条件概率分布,记作 \(P(X=x_i|Y=y)\)。
在此条件下,\(X\) 的期望被称为条件期望,记作 \(E(X|Y=y)\)。
对于条件期望 \(E(X|Y)\),有公式:
这就是全期望公式。
方差与标准差:
在统计意义下,设一组数据 \(\{a_i\}\) 的平均值为 \(\displaystyle \bar{a}=\dfrac{1}{n}\sum^{n}_{i=1}a_i\),则将
叫做这组数据的方差。也定义
为这组数据的标准差。
方差反映了数据的离散程度。方差越小,反映数据越集中。例如在下面两组数据中:
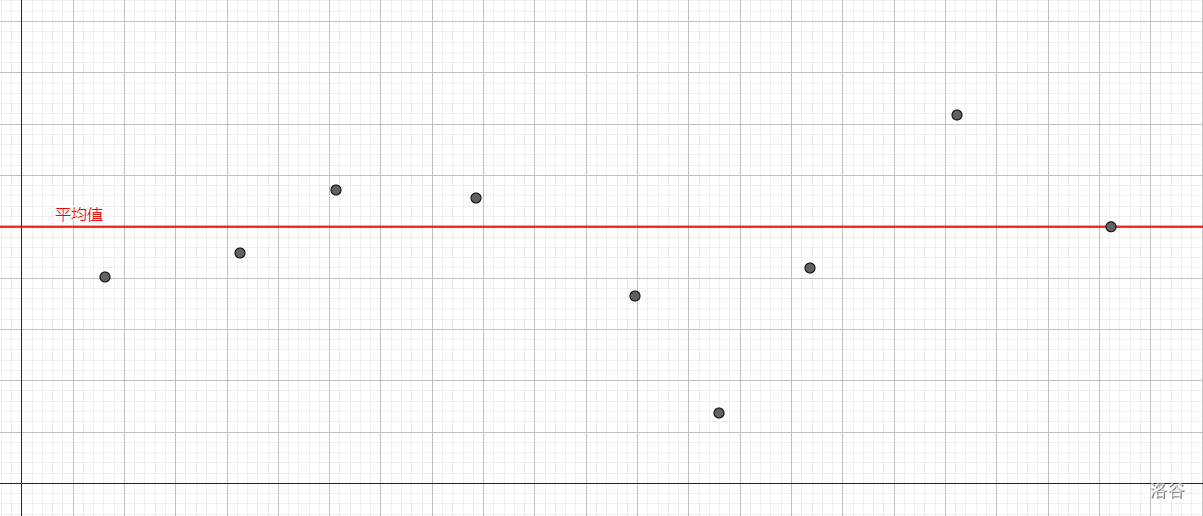
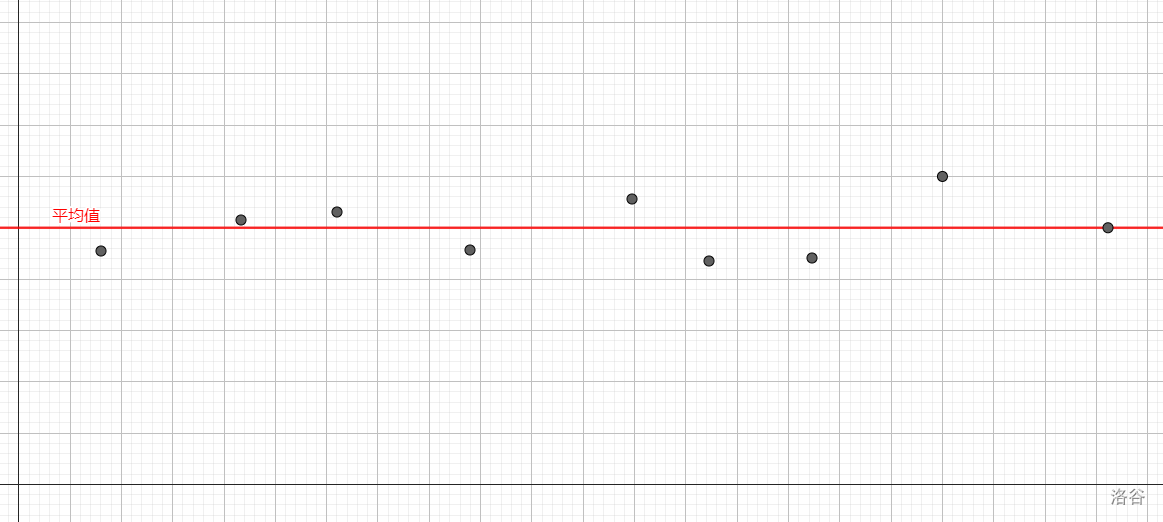
明显下图的数据更集中,因此其方差更小。
在期望意义下,若随机变量 \(X\) 的期望 \(E(X)\) 存在,且期望
也存在,则称其为随机变量 \(X\) 的方差。也定义方差的算术平方根
为随机变量 \(X\) 的标准差。
方差具有如下性质:
- \(\forall a,b\in \mathbf{R}\),\(D(aX+b)=a^2D(X)\);
- \(D(X)=E(X^2)-E(X)^2\);
- \(D(X)\geq 0\);
- 当随机变量 \(X,Y\) 独立时,有 \(D(X\pm Y)=D(X)\pm D(Y)\)。
协方差:
对于随机变量 \(X,Y\),定义
为 \(X\) 与 \(Y\) 的协方差。
协方差具有以下性质:
- 对于随机变量 \(X,Y\),有 \(\text{Cov}(X,Y)=\text{Cov}(Y,X)\);
- 对于随机变量 \(X,Y,Z\),有 \(\forall a,b\in \mathbf{R}\),\(\text{Cov}(aX\pm bY,Z)=a\text{Cov}(X,Z)\pm b\text{Cov}(Y,Z)\);
- \(D(X)=\text{Cov}(X,X)\);
- \(D(X\pm Y)=D(X)\pm 2\text{Cov}(X,Y)+D(Y)\)。
相关系数:
对于随机变量 \(X,Y\),定义
为随机变量 \(X\) 与 \(Y\) 的 Pearson 相关系数。
Pearson 相关系数描述了两个随机变量之间线性相关的紧密程度。\(|\rho_{X,Y}|\) 越大,则 \(X\) 与 \(Y\) 之间的线性相关程度越高。
Pearson 相关系数有如下性质:
- \(\rho_{X,Y}\leq 1\);
- 当 \(\exists a,b\in \mathbf{R},b>0\) 使得 \(P(X=a+bY)=1\) 时,\(\rho_{X,Y}=1\);
- 当 \(\exists a,b\in \mathbf{R},b<0\) 使得 \(P(X=a+bY)=1\) 时,\(\rho_{X,Y}=-1\);
当 \(\rho_{X,Y}=0\) 时,我们称随机变量 \(X,Y\) 不相关,此时 \(X\) 和 \(Y\) 之间不存在线性关系。
概率不等式
布尔不等式:对于随机事件 \(A_1,A_2,...,A_n\),有
\[\boxed{P\left( \bigcup^{n}_{i=1}A_i \right)\leq \sum^{n}_{i=1}P(A_i)} \]
马尔科夫不等式:设 \(X\) 是一个取值非负的随机变量,则 \(\forall a>0\),
\[\boxed{P(X\geq a)\leq \dfrac{E(X)}{a}} \]
切比雪夫不等式:设随机变量 \(X\),则 \(\forall a>0\),
\[\boxed{P(|X-E(X)|\geq a)\leq \dfrac{D(X)}{a^2}} \]特别地,当 \(a=k\sigma(X)\) 时,
\[\boxed{P(|X-E(X)|\geq k\sigma(X))\leq \dfrac{1}{k^2}} \]
切尔诺夫不等式:设随机变量 \(X\),则 \(\forall t>0\),有
\[\boxed{P(X\geq a)=P(e^{tX}>e^{ta})\leq \dfrac{E(e^{tX})}{e^{ta}}} \]\(\forall t<0\),有
\[\boxed{P(X\leq a)=P(e^{tX}>e^{ta})\leq \dfrac{E(e^{tX})}{e^{ta}}} \]
概率与期望 DP
简介:由于概率和期望具有线性性质,使得可以在概率和期望之间建立一定的递推关系,这样就可以通过动态规划来解决一些概率问题,例如概率和期望的最值问题就常常使用概率 DP、期望 DP 来解决。
概率 DP:
概率 DP 通常已知初始的状态,然后求解最终达到目标的概率,因此概率 DP 需要顺序求解。
状态转移方程相较于期望 DP 一般比较简单,当前状态只需加上所有上一状态后乘以转移概率即可,即:
而边界就是极端情况下的答案。
例题:P2719 搞笑世界杯
分析:本题有两种做法,一种 DP 递推,一种组合推导。
- \(\text{Solution1: }\) 我们可以这样设计状态:设 \(f(i,j)\) 为还剩下 \(i\) 张 A 类票,\(j\) 张 B 类票后两人买到票相同的概率。
则上一状态有两类,一种是上一人抽到 A 类票,一种是上一人抽到 B 类票。因此 \(f(i,j)\) 分别从 \(f(i-1,j)\) 和 \(f(i,j-1)\) 转移,且转移概率为 \(p(i)=\dfrac{1}{2}\),因此有状态转移方程:
初始状态是 \(\forall 2\le i\le n,f(i,0)=f(0,i)=1\),即当只剩下一种票时概率为 \(1\)。最终答案为 \(f(n,n)\)。
代码如下(\(O(n^2)\)):
#include<bits/stdc++.h>
using namespace std;
const int N = 1250 + 10;
int n;
double f[N][N];
int main()
{
cin >> n;
n /= 2;
for(int i = 2; i <= n; i ++)
f[i][0] = f[0][i] = 1.0;
for(int i = 1; i <= n; i ++)
for(int j = 1; j <= n; j ++)
f[i][j] = f[i - 1][j] / 2 + f[i][j - 1] / 2;
printf("%.4lf", f[n][n]);
return 0;
}
- \(\text{Solution2: }\) 本题还可以通过排列组合的方式推式子,过程不细说了,有兴趣的读者可以自己推一下,答案为 \(1-\dfrac{(2n-2)!}{4^{n-1}[(n-1)!]^2}\)。
代码如下(\(O(n)\)):
#include<bits/stdc++.h>
using namespace std;
int n;
double p;
int main()
{
cin >> n;
n /= 2;
p = 1.0000;
for(int i = 1; i < n; i ++)
p = p * (i + n - 1) / (i << 2);
printf("%.4lf", 1 - p);
return 0;
}
期望 DP:
当求解达到某一目标的期望花费时,由于最终的花费无从知晓(无法从无穷推起),因此期望 DP 不同于概率 DP,需要倒序求解。
期望 DP 一般而言可以这样设计状态:设 \(f(i)\) 为状态 \(i\) 下实现目标的期望值,即到 \(f(i)\) 这个状态的差距是多少。
边界为 \(f(n)=0\),然后进行状态转移,新的状态为上一状态与转移概率的乘积再加上转移的花费,既有:
答案为 \(f(0)\)。
需要注意的是,当转移关系不成环时,期望 DP 可以进行线性递推,但当转移关系成环时,期望 DP 的最终状态相当于一个已知量,而转移关系相当于一个个方程,此时需要使用高斯消元法来解决。
例题:P4316 绿豆蛙的归宿
题意:给定一个 DAG,求起点到终点的路径长度期望。
分析:设状态 \(f(i)\) 表示点 \(i\) 到终点 \(n\) 的期望路径总长。则边界为 \(f(n)=0\),要求的答案为 \(f(1)\)。
考虑一条有向边 \(i\to j\),则有:
其中,转移概率 \(p(i)\) 其实就为结点 \(i\) 的度数的倒数,即 \(p(i)=\dfrac{1}{d(i)}\)。
我们可以发现,上述转移过程与图上有向边的方向恰好相反,因此我们可以建反图,然后用一次拓扑排序来方便我们递推。
上述算法瓶颈在于拓扑排序,时间复杂度为 \(O(n+m)\)。
代码如下:
#include<bits/stdc++.h>
using namespace std;
const int N = 1e5 + 10;
int n, m;
int e[N * 2], ne[N * 2], h[N * 2], w[N * 2], idx;
int din[N], d[N];
double f[N];
inline void add(int a, int b, int c)
{
e[idx] = b, ne[idx] = h[a], w[idx] = c, h[a] = idx ++;
}
void topsort()
{
queue<int> q;
q.push(n);
while(q.size())
{
int u = q.front();
q.pop();
for(int i = h[u]; ~i; i = ne[i])
{
int j = e[i];
f[j] += (f[u] + w[i]) / d[j];
if(-- din[j] == 0) q.push(j);
}
}
}
int main()
{
memset(h, -1, sizeof h);
cin >> n >> m;
for(int i = 1; i <= m; i ++)
{
int u, v, wi;
scanf("%d%d%d", &u, &v, &wi);
add(v, u, wi);//建反图
din[u] ++, d[u] ++;
}
topsort();
printf("%.2lf", f[1]);
return 0;
}
在概率与期望 DP 的实际应用中,如果定义的状态转移方程存在后效性问题,需要用到高斯消元来优化。概率与期望 DP 也会结合其他知识进行考察,例如状态压缩,树上进行 DP 转移等。
Part6 博弈论
博弈论主要研究的是在一个游戏中,进行游戏的多位玩家的策略,是经济学与应用数学学科的一个分支。
Nim 博弈
定义:给定 \(n\) 堆物品,第 \(i\) 堆物品有 \(A_i\) 个。两名玩家轮流行动,每次可以任选一堆,取走任意多个物品,可把一堆取光,但不能不取。取走最后一件物品者获胜。两人均采取最优策略,问先手能否必胜。我们把这种游戏称为 Nim 博弈。
基本概念:
局面:我们把 Nim 博弈游戏过程中面临的状态称为局面。
先手与后手:整局游戏第一个行动的称为先手,第二个行动的称为后手。
必胜局面与必败局面:若在某一局面下存在某种行动,使得行动后对手面临必败局面,则称这样的局面为必胜局面;若在某一局面下无论采取何种行动,都会输掉游戏,则称这样的局面为必败局面。
Nim 博弈不存在平局,只有先手必胜和先手必败两种情况。
Nim 定理:
内容:记 \(\displaystyle A=\bigoplus^{n}_{i=1}A_i\),Nim 博弈先手必胜,当且仅当 \(A\neq 0\)。
证明:数学归纳法。
所有物品被取光是一个必败局面,此时显然有 \(A=0\)。
对于任意一个局面,如果 \(A\neq 0\),设 \(A\) 的二进制表示下最高位的 \(1\) 在第 \(k\) 位,那么至少存在一堆物品 \(A_i\),它的第 \(k\) 位是 \(1\)。显然 \(A_i\oplus A<A_i\),我们就从 \(A_i\) 堆中取走若干物品,使其变为 \(A_i\oplus A\),就得到了一个各堆物品数量异或和为 \(0\) 的局面。
对于任意一个局面,如果 \(A=0\),那么无论如何取物品,得到的局面下各堆物品数量异或和一定不为 \(0\)。可以用反证法证明,假设 \(A_i\) 被取成了 \(A^{'}_i\),并且 \(A_1\oplus A_2\oplus ...\oplus A^{'}_i\oplus ...\oplus A_n=0\),由异或运算性质知 \(A_i=A^{'}_i\),与 Nim 博弈游戏规则(不能不取)矛盾。
综上所述,由数学归纳法可知,\(A\neq 0\) 为必胜局面,一定存在一种行动使得对手面临“各堆物品数量异或和为 \(0\)”的局面。\(A=0\) 为必败局面,无论如何行动,都会让对手面临一个“各堆物品数量异或和不为 \(0\)”的必胜局面。
板子题。根据 Nim 定理,当石子数量异或和不为 \(0\) 时,存在先手必胜策略,反之不存在。
代码如下(时间复杂度 \(O(Tn)\)):
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N = 1e4 + 10;
int T, n;
int a[N];
int Nimsum;//Nim和
signed main()
{
cin >> T;
while(T --)
{
Nimsum = 0;
cin >> n;
for(int i = 1; i <= n; i ++)
{
scanf("%lld", &a[i]);
Nimsum ^= a[i];
}
if(Nimsum != 0) puts("Yes");
else puts("No");
}
return 0;
}
公平组合游戏(ICG)与有向图游戏
公平组合游戏(ICG):
若一个游戏满足:
- 由两名玩家交替行动;
- 在游戏进程的任意时刻,可以执行的合法行动与轮到哪名玩家无关;
- 不能行动的玩家判负。
则称该游戏为公平组合游戏(ICG)。
Nim 博弈是一种公平组合游戏。
有向图游戏:
定义:给定一个 DAG,图中有一个唯一的起点,在起点上放有一枚棋子。两名玩家交替地把这枚棋子沿有向边进行移动,每次可以移动一步,无法移动者判负。该游戏被称为有向图游戏。
任何一个公平组合游戏都可以转化为有向图游戏。具体方法是:把每个局面看成图中的结点,并且从每个局面向沿着合法行动能够到达的下一个局面连有向边。
博弈图:类似有向图游戏地,将博弈中所有可能的局面(状态)按递推关系画成一张 DAG,就是博弈图。
\(\text{mex}\) 运算与 \(\text{SG}\) 函数
\(\text{mex}\) 运算:
定义:设非空整数集 \(S\),定义 \(\text{mex}(S)\) 为求出不属于 \(S\) 的最小非负整数的运算。
用公式表达为:
\(\text{SG}\) 函数:
定义:在有向图游戏中,对于每个结点 \(x\),设从 \(x\) 出发共有 \(k\) 条有向边,分别到达结点 \(y_1,y_2,...,y_k\),定义函数 \(\text{SG}(x)\) 为 \(x\) 的后继结点 \(y_1,y_2,...,y_k\) 的 \(\text{SG}\) 函数值构成的集合再执行 \(\text{mex}\) 运算的结果。
用公式表达为:
特别地,整个有向图游戏 \(G\) 的 \(\text{SG}\) 函数值被定义为有向图游戏起点 \(s\) 的 \(\text{SG}\) 函数值,即:
有向图游戏的和:
设 \(G_1,G_2,...,G_m\) 是 \(m\) 个有向图游戏。定义有向图游戏 \(G\),它的行动规则是任选某个有向图游戏 \(G_i\),并在 \(G_i\) 上行动一步。\(G\) 被称为有向图游戏 \(G_1,G_2,...,G_m\) 的和。
有向图游戏的和的 \(\text{SG}\) 函数值等于它包含的各个子游戏 \(\text{SG}\) 函数值的异或和,即:
有向图游戏的胜负判定:
定理:有向图游戏的某个局面必胜,当且仅当该局面对应结点的 \(\text{SG}\) 函数值大于 \(0\);有向图游戏的某个局面必败,当且仅当该局面对应结点的 \(\text{SG}\) 函数值等于 \(0\)。
证明与 Nim 博弈方法类似。

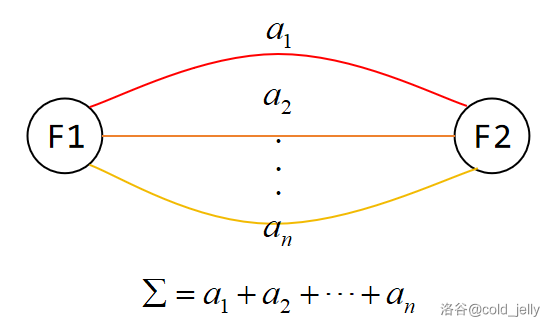
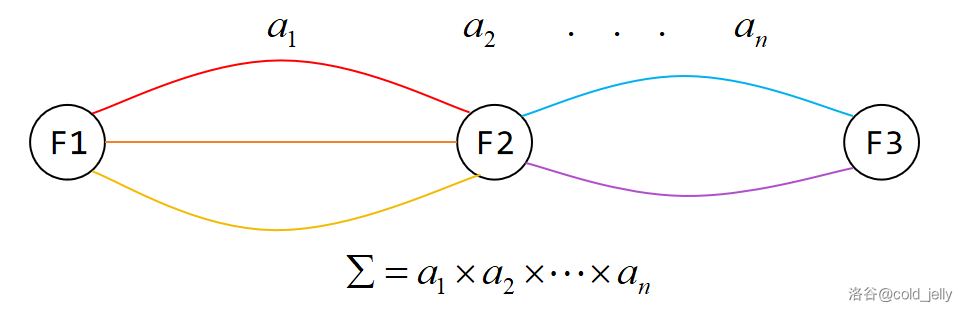

 浙公网安备 33010602011771号
浙公网安备 33010602011771号