其他回归方法(基于分类的方法)
非线性回归方法:
- K近邻回归(KNN Regression)
- 支持向量回归(Support Vector Regression)
- 决策树回归
- 样条回归
- 径向基网络
- 高斯过程
K近邻回归:
通过按距离排序找出一个样本的k个最近邻居,将这些邻居的标签的平均值或加权平均值(权重通常为距离的倒数)赋给该样本,便可得到该样本的预测值。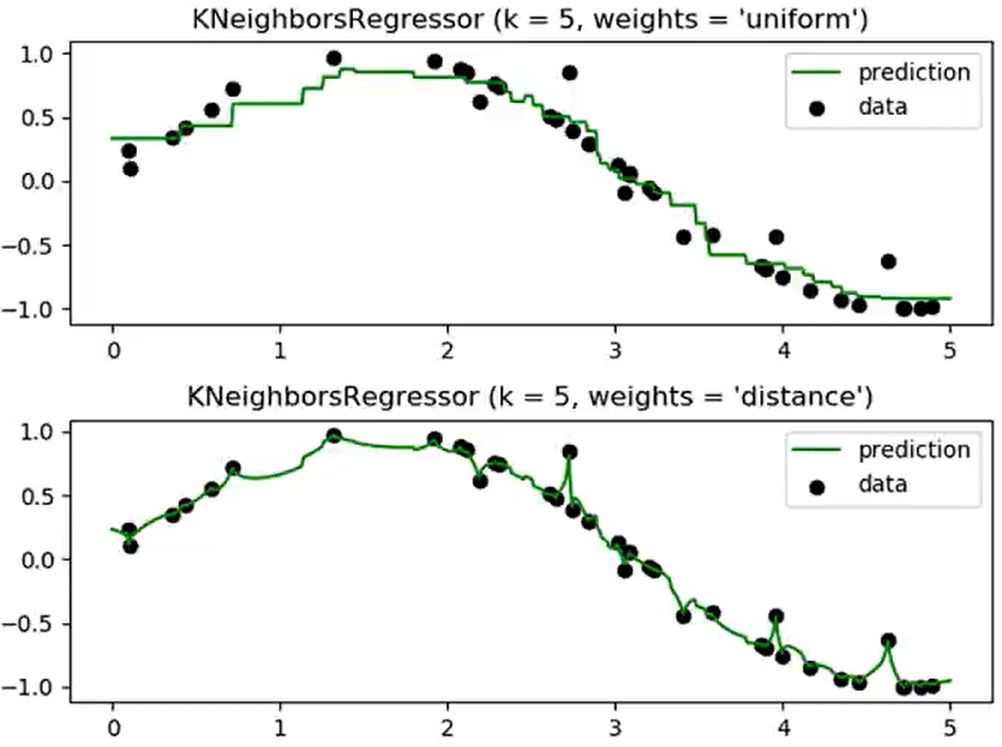
参数:
n_neighbors:邻居数k,默认为5;
weights:样本权重,默认为‘uniform’(样本权重相同),还可选择‘distance’(距离倒数加权);
algorithm:用于寻找邻居的算法,默认为‘auto’(自动选取最优算法)。还可选择‘ball tree’(X是高维时优秀) ‘kd_tree’ 'brute'(暴力搜索)
p:Minkowski指标的幂参数,默认p=2(欧氏距离),还可选择p=1(曼哈顿距离)
metric:距离度量指标,默认为‘minkowski’(闵式距离)
闵式距离计算公式: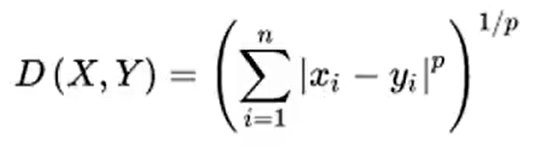
决策树回归:
基于树状结构,通过贪婪算法对自变量空间进行划分,划分依据为各空间的均方误差(或绝对误差等)之和最小;
参数:
criterion:分裂质量的评价函数,默认为‘mse’(均方误差),还可选择‘friedman_mse’(弗里德曼改进均方误差)‘mae’(绝对误差);
splitter:每个节点的拆分策略,默认为‘best’(最优拆分),还可选择‘random’(最优随机拆分);
max_depth:树的最大深度;
min_sample_split:拆分内部节点所需要的最小样本数;
min_impurity_decrease:如果该分裂导致杂质的减少大于或等于该值,则分裂节点;
min_impurity_split:早期树木停止增长的阈值;
属性:
feature_importances_:特征重要性;
tree_:决策树对象;
用KNN回归和DT回归预测架设所需的电线长度;
数据集: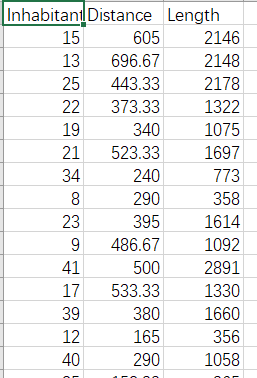 ,inhabitant(居民数)、distance(距离),length(所需电线长度);
,inhabitant(居民数)、distance(距离),length(所需电线长度);
#加载数据
import pandas as pd data = pd.read_csv(r'C:\Users\Liujiangchuan\Desktop\Work_zone\Electrical_Length .csv') data.info()

可以看见,数据集没有缺失,可以直接分离自变量和因变量先进行数据集划分再进行模型构建;
from sklearn.neighbors import KNeighborsRegressor from sklearn.model_selection import train_test_split X = data.copy().drop(['Length'], axis=1) y=data['Length'] train_X,test_X,train_y,test_y = train_test_split(X, y, test_size = 0.2)
knr = KNeighborsRegressor()
knr.fit(train_X, train_y)
#求训练集和测试集决定系数
print("测试集决定系数:%s"%round(knr.score(train_X,train_y),4))
print("训练集决定系数:%s"%round(knr.score(test_X,test_y),4))
#K近邻回归调参
#对weight/n_neighbors参数遍历调参
#生成元组列表
import numpy as np
neighbors = np.linspace(2, 15, 14).astype(int)
weights = ['uniform','distance']
parameters = [(neighbor,weight) for neighbor in neighbors for weight in weights]
parameters[:5]
test_score={}
for parameter in parameters:
test_score[parameter]=[parameters]
test_score[parameter]=KNeighborsRegressor(n_neighbors=parameter[0],weights=parameter[1]).fit(train_X,train_y).score(test_X,test_y)
k_result = pd.DataFrame(list(test_score.items()),columns = ['parameter','test_score'])
k_result
结果:
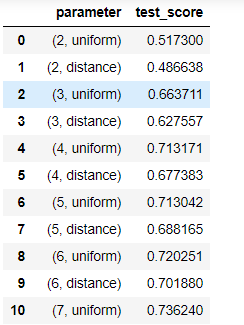
用DecisionTreeRegression来构建模型并预测:
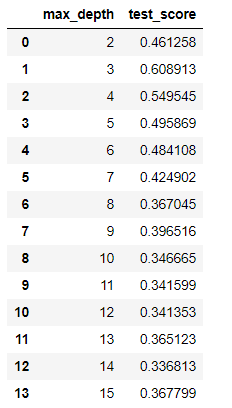
import pandas as pd import numpy as np #加载数据 data = pd.read_csv(r'C:\Users\Liujiangchuan\Desktop\Work_zone\Electrical_Length .csv') #分离变量 X = data.copy().drop(['Length'],axis=1) y = data['Length'] #构建模型并进行预测 from sklearn.tree import DecisionTreeRegressor from sklearn.model_selection import train_test_split train_X, test_X, train_y, test_y = train_test_split(X, y, test_size = 0.3) dtr = DecisionTreeRegressor( max_depth = 5) dtr.fit(train_X, train_y) print('训练集决定系数:%s'%round(dtr.score(train_X,train_y),4)) print('测试集决定系数:%s'%round(dtr.score(test_X,test_y),4)) print('特征重要性:%s' %dtr.feature_importances_) #对max_depth参数遍历调参 max_depth = np.linspace(2,15,14).astype(int) test_score={} for n in max_depth: test_score[n]=DecisionTreeRegressor(max_depth=n).fit(train_X,train_y).score(test_X,test_y) dtr_result=pd.DataFrame(list(test_score.items()),columns=['max_depth','test_score']) dtr_result
结果: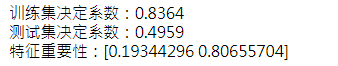


 浙公网安备 33010602011771号
浙公网安备 33010602011771号