机器学习实战案例:共享单车时租预测
案例描述:市场上推出了某款共享单车,运营了一段时间,得到了一系列影响租车因素的数据和当天的租车数量,请你根据这些数据,进行回归分析,预测以后某天的共享单车时租适量,方便公司投放以获取最大收益。
案例数据集:Bike_Sharing_data
字段说明:
| datetime | 详细到小时的日期+时间戳 |
| season | 季节 1:春天, 2:夏天, 3:秋天, 4:冬天 |
| holiday | 是否是公共假期 |
| workingday | 是否是工作日(不是周末也不是公共假期) |
| weather | 天气情况 1:无云,少量云,部分多云 2:雾+多云,雾+云散开,雾+少云,雾 3:小雪,小雨+雷暴+散云,小雨+散云 4:暴雨+冰雹+雷暴+雾,雪+雾 |
| temp | 以摄氏度为单位的温度 |
| atemp | 以摄氏度为单位的体感温度 |
| humidity | 相对湿度 |
| windspeed | 风速 |
| casual | 未注册用户租赁数量 |
| registered | 注册用户租赁数量 |
| count | 租赁自行车总数,包括未注册和注册 |
首先先导入一些基础的工具包方便我们读取分析数据。
import numpy as np import pandas as pd
接下来我们导入我们要使用的数据集,利用pandas工具包下read_csv()函数,里面放进文件的地址并显示数据前5行。
dataDaily=pd.read_csv(r'C:\Users\Liujiangchuan\Desktop\Work_zone\train.csv') dataDaily.head(2)
我们可以看到数据集的部分内容:

接下来我们对数据集中的缺失值进行检测,缺失值就是数据集中因为某些人为或者失误导致没有数据的情况下,利用isnull()函数可以显示所有数据的完整性,但是如果数据集过大,输出可能不完整,就会导致你看不见部分数据是否缺失,出现以下的情况,中间的数据全是省略号。
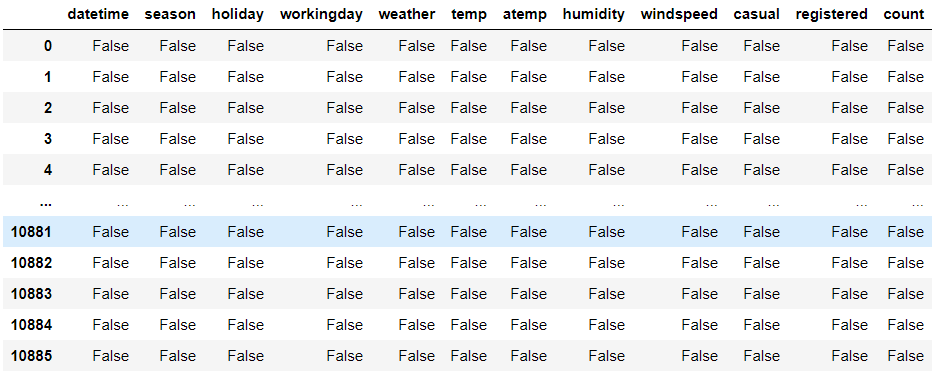
我们可以使用sum()函数对所有缺失值进行统计,方便我们查看每一列数据是否缺失数据。
dataDaily.isnull().sum()
或者我们可以使用info()函数,显示每一列数据的情况:
dataDaily.info()
我们来看看数据集的情况:
dataDaily.describe()
结果分别如下:
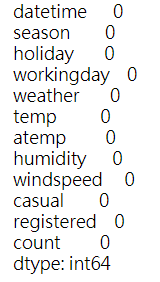
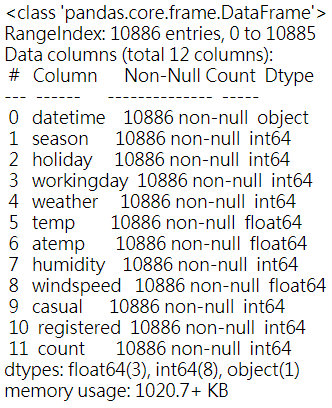
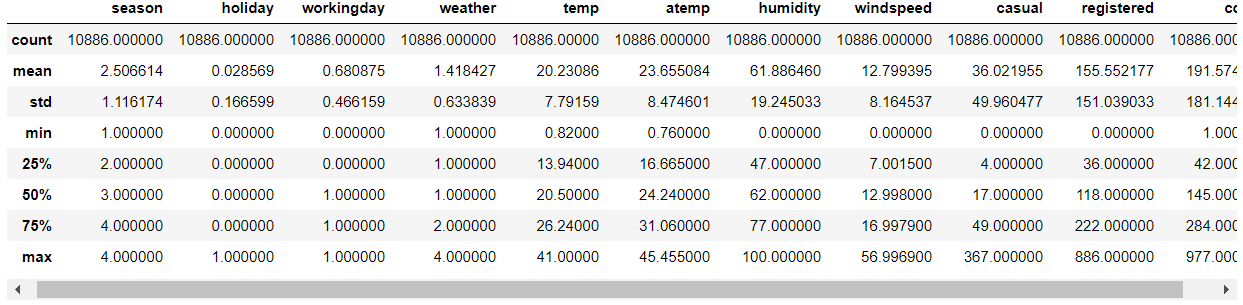
这里我们可以看到数据集是完整的,每一列都没有缺失值。如果出现缺失值,推荐看看这篇文章对缺失值进行简单处理:机器学习:缺失值处理方法。
接下来,我们利用几个工具包对数据集进行可视化处理,便于我们更好的分析数据。
先导入要使用的工具包
import seaborn as sn import matplotlib.pyplot as plt %matplotlib inline #让图形嵌入网页(我使用的是anaconda) dataDaily.plot(subplots=True,figsize=(10,20))
利用plot函数绘制数据集每一列的折线图。由于数据太多了,我这里就截取前半部分输出结果。
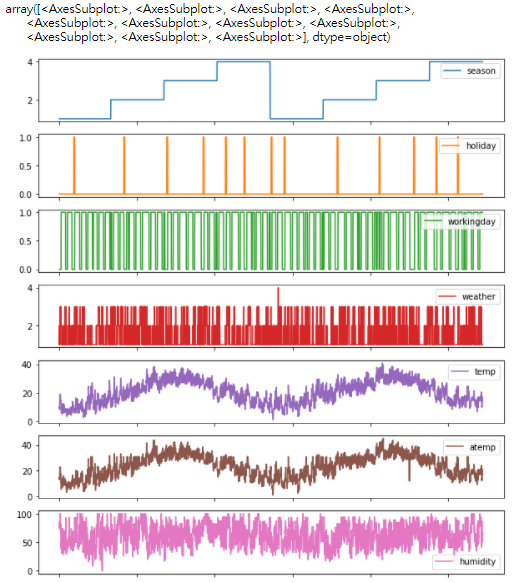
接下来我们对部分数据数据进行相关分析,相关分析是研究两个或两个以上处于同等地位的随机变量间的相关关系的统计方法,例如人的身高和体重之间关系,空气中湿度和降雨量之间的关系。这里我们使用seaborn里面的热力图对count、weather、humidity、temp、registered、atemp、windspeed、casual之间的相关性进行分析
corrMat=dataDaily[['temp','humidity','windspeed','registered','casual','atemp','count']].corr() sn.heatmap(corrMat,annot=True)
现在给出我使用的参数annot;
annot(annotate的缩写):默认取值False;如果是True,在热力图每个方格写入数据;如果是矩阵,在热力图每个方格写入该矩阵对应位置数据。
关于heatmap()参数一共有十几个,这里我就不一一介绍了,如有兴趣可以去查看官方给出的API介绍。
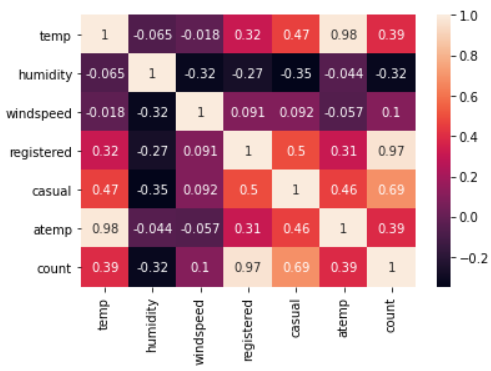
热力图数值越高代表两者相关性越强。从图中我们可以看出:
-
temp温度和humidity湿度特征分别与count呈正负相关。它们之间的相关性不明显,count对temp温度和humidity湿度的依赖性仍然很小。 -
windspeed不是真正有用的数字特征,这可以从它和count的相关值看出来。 -
atemp将不被采纳,因为atemp和temp彼此之间具有很强的相关性。在模型构建期间,必须删除二者其中一个变量,因为它们将在数据中表现出多重共线性。 -
casual未注册用户租赁数量和registered注册用户租赁数量也没有被考虑在内,因为它们本质上是leakage variables泄漏变量(二者相加等于count),需要在模型构建时丢弃。
然后我们确定要删除的特征:
dropFeatures=['casual','registered','atemp','datetime'] #可能导致leakage variable(泄露变量)(casual和registered两者相加等于count) #atemp与temp具有很强关联性 #datetime在建模过程中舍弃(无效特征)
下面我们提取相关特征进行建模:
X=dataDaily.copy().drop(dropFeatures,axis=1) #count相当于因变量,只出现在y中,应该在X中被删除 X=X.copy().drop('count',axis=1) yLabel=dataDaily['count'] X.info() #显示X数据的情况
结果如下:

接下来划分训练-测试数据集:训练(0.7)-测试(0.3),然后构建线性回归模型。
#训练-测试数据集划分 from sklearn.model_selection import train_test_split train_x,train_y,test_x,test_y=train_test_split(X,yLabels,test_size=0.3,random_state=42) #这里的random_state主要是为了训练的可重复性,若不设置random_staste则每次训练结果不一样 #构建模型进行训练 from sklearn.linear_model import LinearRegression Model=LinearRegression() #构建模型 Model.fit(X=train_x,y=train_y) #模型训练 preds=Model.predict(X=test_x) #模型预测
我们可以通过计算MSE(mean-squared-error)均方误差或者对预测结果模型可视化来判断预测结果的好坏。
from sklearn.metrics import mean_squared_error print("Linear Regression Mean-squared-error:",mean_squared_error(preds,test_y)) #结果可视化 plt.plot(preds) #查看预测时租数量的折线图 plt.plot(np.array(test_y)) #对比真实值
结果如下:(左图为预测值,右图为真实值)
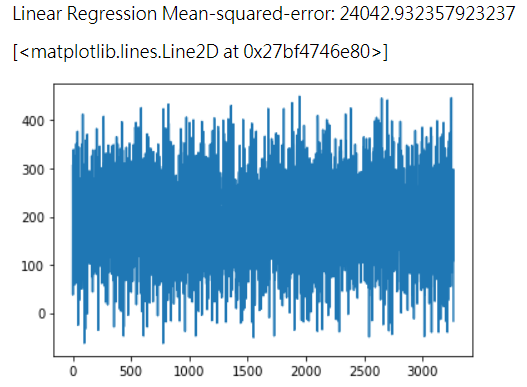
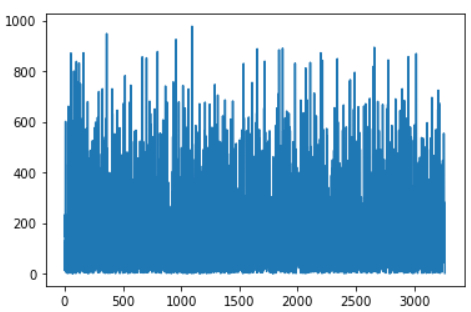
从图中我们可以看出,居然出现了某些时间段的预测投放数量是负值,这显然是不符合常理的,下面我们对训练模型进行优化。
这里我们引入RMSLE(Root Mean Squared Logarithm Error)均方根对数误差,RMSLE惩罚欠预测大于过预测,适用于某些需要欠预测损失更大的环境。
我们可以有如下假设:某天共享单车的需求量为1000辆,当预测值分别是600和1400的时候,RMSE和RMSLE指标数值:RMSE在两种预测情况下的值都是400,而RMSLE在预测值为600时的值是0.510,在预测值为1400时的值为0.336。可以看出,RMSLE对欠预测的惩罚大于过预测。
我们还有一种情况可以使用RMSLE指标。当预测值的范围很大的时候,RMSE会被一些很大的值所主导,这样的话,及时当预测值很小的时候你能预测准确,但是如果非常大的值你不能预测准确,就会导致RMSE很大,相对于此,先取对数再求RMSE的RMSLE可以解决这个问题。
这里给出RMSLE的计算公式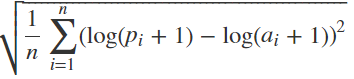
其中:n 是测试集中的小时数;pi 是预测的自行车租用数量;ai 是实际的自行车租用数量;log(x) 是自然对数。
下面我们定义计算RMSLE的函数:
def rmsle(preds,test_y) log1=np.array([np.log1p(v) for v in preds]) log2=np.array([np.log1p(v) for v in test_y]) calc=(log1-log2)**2 return np.sqrt(np.mean(calc))
这里的log1p函数即为log(x+1),避免出现负数结果。我们利用log1p函数对线性回归模型进行优化。
IModel = LinearRegression() IModel.fit(X=train_x,y=np.log1p(train_y)) preds=IModel.predict(X=test_x) print("RMSLE :", round(rmsle(expm1(preds),test_y),4) #这里得出的preds是取了对数以后的值,我们需要通过log1p的逆函数expm1得到实际的preds值,方便带入rmsle函数计算均方根对数误差。round函数在这里是控制输出范围,4位保留四位小数。
现在我们来看看修改模型后的结果:
plt.plot(np.expm1(preds))
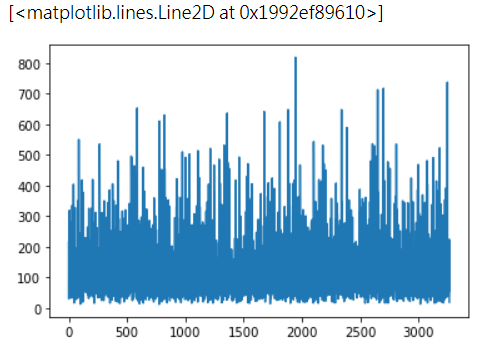
可以看到所有的预测值都是正数了。
这个案例的预测数大概到达了不错的效果;当然如果我们想进一步优化预测效果,我们可以对数据进行离散化和特征编码,得到更好的预测结果,我也会继续更新优化过程~


 浙公网安备 33010602011771号
浙公网安备 33010602011771号