机器学习：回归分析方法整理

　目前为止，在机器学习的过程中，回归分析由如下几部分构成：

1. 线性回归（LinearRegression）：这一类问题就是我们高中所学习过的回归问题。我们常使用最小二乘法逼近进行拟合，有时候也使用最小化“拟合缺陷”（最小绝对误差回归）或者在桥回归中最小化最小二乘损失函数的惩罚；拟合方程：一般来说，线性回归都可以通过使用最小二乘法求出其方程，计算出对于y=bx+a的直线，一般的，影响y的因素不止一个，设有x1，x2，...，xk，k个因素，考虑如下的线性关系式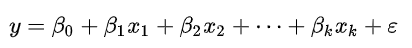：对y与x1，x2，...，xk同时作n次独立观察得n组观测值（xt1，xt2，...，xtk），t=1,2，...，n（n>k+1）,满足关系式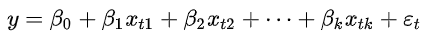：       ，其中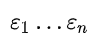                互不相关均是与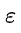同分布的随机变量，为了用矩阵表示上式，令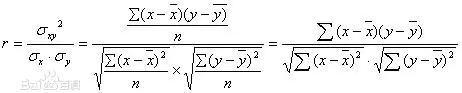：，于是有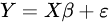，使用最小二乘法得到β的解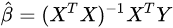：，其中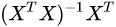称为X的伪逆矩阵。
2. 诊断回归（Regression Ddiagnostics）：它是对回归分析中的假设及数据的检验与分析，通常包含两方面的内容：1）检验回归分析中假设是否合理，如在线性回归模型中，通常假设随机误差之间独立，期望为零及方差相同，或者进一步假设它们服从正态分布，回归诊断就是为了检验这些假设是否合理，如果不合理，如何对数据进行怎样的修正后，能使它们满足这些假设；2）对数据进行诊断，检验观测值中是否有异常数据，有异常数据如何处置。回归诊断主要探究的问题有：1）残差是否为随机性、是否为正态性、是否不为异方差；2）高度相关的自变量是否引起了共线性；3）模型的函数形式是否错误或在模型中是否缺少重要的自变量；4）样本数据中是否存在异常值。
3. 回归变量的选择（Regression Variable Selection）：选择变量有两种办法：全模型（Full model）：将所有对因变量有影响的m个因素都选入做回归；或者选模型（Selected model）：从所有因素中挑出p个因素做回归。一般来说选模型比全模型好构造的多，所以我们往往会想牺牲一些性质换取一个更好的结果。
4. 参数估计方法（Parameter Estimation）：我们在概率论与数理统计中学过：参数估计方法有两种，1.点估计，2.区间估计；常见的点估计方法：矩估计，最小二乘估计。极大似然估计，贝叶斯估计；常见的区间估计方法：利用已知的抽样分布，利用区间估计与假设检验的联系，利用大样本理论。我们在机器学习中主要利用三种估计方法：主成分回归（Principle Component Regression）：将主成分变量作为自变量进行回归分析，然后根据分系数矩阵将原变量代回得到的新的模型；偏最小二乘回归（Partial least squares Regression）：通过投影分别将预测变量和观测变量投影到一个新空间，来寻找线性回归模型；岭回归（Ridge Regression）：用于共线性数据分析的有偏估计回归方法，实质上是一种改良的最小二乘估计法，通过放弃最小二乘法的无偏性，以损失部分信息降低精度为代价获得回归系数更为符合实际更可靠的的回归方法。对病态数据的拟合要强于最小二乘法。
5. 非线性回归（Non-linear Regression）：回归函数关于未知回归系数具有非线性结构的回归。常用的处理方法有：回归函数的线性迭代法、分段回归法、迭代最小二乘法等，非线性回归分析与线性回归分析相似。
6. 含定性变量的回归：包含：只有一个虚拟变量的回归，含有多个虚拟变量的回归，分段回归。虚拟变量：即只取0和1两个值的变量。

　　现实中常用的回归分析有：线性回归、逻辑回归和岭回归。

参考来源：百度百科