算法随笔——平衡树Treap

平衡树定义

先解释下平衡树，当时找资料找了半天才完全搞懂。
上图：

image

平衡树 = 平衡二叉树
平衡树 = 二叉搜索树 + 不同平衡树对于平衡的定义
而“平衡性”是为了使整体的查询高度满足在 \(O(\log n)\) 。

Treap 定义

这一篇是平衡树中的 Treap 树，最简单的平衡树之一。

首先这是一颗二叉搜索树，满足 BST 性质（即左节点 < 当前节点 < 右节点），但如何保证其复杂度呢？就需要用到 Treap 中的左旋、右旋了，上图：

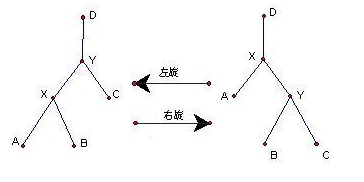
image

可以发现旋转过程中并没有改变平衡树的二叉搜索树的性质，因此可以通过一定的旋转让树的深度保持在 \(O(\log n)\) 左右，使树更加平衡。

怎么做到呢？我们发现在随机数据下二叉搜索树是几乎接近平衡的，而 Treap 就是利用随机的思想创造平衡。可以在维护整个树时顺便给每个节点一个随机值，强行给其加入堆的性质，让每个节点的额外权值大于其子节点的额外权值。

这就是 Treap 的来源（Treap = tree + heap），本质上是一棵随机权值满足大根堆性质的 BST，可以以 \(O(\log n)\) 的时间复杂度完成检索、插入、求前驱后继、删除节点等操作。

问题描述

P3369 【模板】普通平衡树

您需要写一种数据结构（可参考题目标题），来维护一些数，其中需要提供以下操作：

  1. 插入一个数 \(x\)。
  2. 删除一个数 \(x\)（若有多个相同的数，应只删除一个）。
  3. 定义排名为比当前数小的数的个数 \(+1\)。查询 \(x\) 的排名。
  4. 查询数据结构中排名为 \(x\) 的数。
  5. 求 \(x\) 的前驱（前驱定义为小于 \(x\)，且最大的数）。
  6. 求 \(x\) 的后继（后继定义为大于 \(x\)，且最小的数）。

对于操作 3,5,6，不保证当前数据结构中存在数 \(x\)。

这道题是平衡树的模板题，直接用 Treap 实现即可。

建树

为了避免边界问题，初始往树中插入 \(-\infty, \infty\) 两个节点，以 \(-\infty\) 为根，$\infty$ 为其右节点。

struct BST
{
	int l,r,val,dat,cnt,size;
}a[N];
int idx,root,n;
// 新增一个节点
int New(int v)
{	
	a[++idx].val = v;
	a[idx].dat = rand();//随机权值
	a[idx].cnt = a[idx].size = 1;//初始为 1
	return idx;
}
void build()
{
	New(-INF);New(INF);
	root = 1,a[1].r = 2;
	update(1);
}

旋转

左旋（\(zag\)）、右旋（\(zig\)）操作可以说是 Treap 树中最重要的部分了，也是 Treap 树的精髓。（zag右zig左也行）
设当前节点是 \(y\),
左旋的过程中可以想象成当前节点的左儿子绕父节点旋转了上来，而 \(y\) 的左儿子由 \(x\) 的右儿子嫁接而来。
右旋也是一样的，只要记住了图，就可以照葫芦画瓢写出 \(zig\)、\(zag\) 的代码了：

void zig(int &p)
{ 
	int q = a[p].l;
	a[p].l = a[q].r,a[q].r = p,p = q; //p 是引用
	update(a[p].r);update(p); // 从下到上更新
}
void zag(int &p)
{
	int q = a[p].r;
	a[p].r = a[q].l,a[q].l = p,p = q;
	update(a[p].l);update(p);
}

插入

题目中给出的数可能重复，可以给每个节点增加一个 \(cnt\)，记录该数出现个数，可以比较方便地处理删除和插入操作。

void insert(int &p,int val)
{
	//找到则新增节点，由于是引用，所以其父节点会自动更新子节点的值
	if (p == 0) {p = New(val);return;} 
	if (val == a[p].val)
	{
		a[p].cnt++;//在树中
		update(p);//更新子树大小
		return;
	}
	if (val < a[p].val) //若小于则在左子树查询
	{
		insert(a[p].l,val);
		if (a[p].dat < a[a[p].l].dat) zig(p); //检查是否满足堆的性质
	}
	else 
	{
		insert(a[p].r,val);
		if (a[p].dat < a[a[p].r].dat) zag(p);
	}
	update(p);//插入完每次更新
}

求前驱/后继

以后继为例，\(val\) 的后继指序列中大于 \(val\) 的最小值。
从值为 \(\infty\) 的节点开始，在树中检索 \(val\)，每经过一个节点就用这个节点更新 \(ans\)。

  • 若没有找到 \(val\)，则当前的 \(ans\) 即为所求。
  • 若找到了 \(val\) 但该节点没有右子树，则 \(ans\) 即为所求。
  • 若找到了 \(val\) 且该节点有右子树，则沿着右子树一直向左走即可得到 \(ans\)。

求后继：

点击查看代码 
int get_next(int val)
{
	int ans = 2; // a[2].val = INF
	int p = root;
	while (p)
	{
		if (val == a[p].val) //检索val
		{
			if (a[p].r > 0) //有右子树
			{
				p = a[p].r;
				while (a[p].l) p = a[p].l;
				ans = p; 
			}
			break; //直接返回ans
		}
		if (a[p].val > val && a[p].val < a[ans].val) ans = p; //满足后继更新答案
		if  (val < a[p].val) p = a[p].l;
		else p = a[p].r;
	}
	return a[ans].val;
}

求前驱：
其实本质是一样的，需要注意的是 \(ans\) 初始是 \(1\)，因为正无穷的 \(idx\) 为 \(1\)。
还有就是找到 \(val\) 后返回的是右子树最左端的节点，正好是和后继反过来的。

点击查看代码 
int get_pre(int val)
{
	int ans = 1;//a[1].val = -INF
	int p = root;
	while (p)
	{
		if (val == a[p].val) 
		{
			if (a[p].l > 0) //有左子树
			{
				p = a[p].l;//返回左子树最右
				while (a[p].r > 0) p = a[p].r;
				ans = p;
			}
			break;//直接返回ans
		}
		if (a[p].val < val && a[p].val > a[ans].val) ans = p;
		if (val < a[p].val) p = a[p].l;
		else p = a[p].r;
	}
	return a[ans].val;
}

删除

由于 Treap 树旋转的性质十分强大，所以我们可以将待删除节点旋转至叶子节点从而直接删除即可。

void remove(int &p,int val)
{
	if (p == 0) return; //树中不存在
	if (val == a[p].val) //找到了
	{
		if (a[p].cnt > 1) 
		{
			a[p].cnt--; 
			update(p);
			return;
		}
		if (a[p].l || a[p].r) //存在子节点
		{
			//只存在左子树 或者 左右都存在但左边随机值更大
			if (a[p].r == 0 || a[a[p].l].dat > a[a[p].r].dat) 
				zig(p),remove(a[p].r,val); //保证了堆的性质
			else zag(p),remove(a[p].l,val);
			update(p);
		}
		else p = 0;//直接删除
		return ;
	}
	if (val < a[p].val) remove(a[p].l,val);
	else remove(a[p].r,val);
	update(p);
}

根据排名查询

int getval(int p,int rank)
{
	if (p == 0) return INF; // 没找到
	if (a[a[p].l].size >= rank) return getval(a[p].l,rank);
	if (a[a[p].l].size + a[p].cnt >= rank) return a[p].val;
	return getval(a[p].r,rank-a[a[p].l].size-a[p].cnt); //在右边
}

根据 \(val\) 查询排名

int get_rank(int p,int val)
{
	if (p == 0) return 0;
	if (val == a[p].val) return a[a[p].l].size + 1;
	if (val < a[p].val) return get_rank(a[p].l,val); //往左查询
	return get_rank(a[p].r,val) + a[a[p].l].size + a[p].cnt; // 往右加上当前左子树
}

完整代码

#include<bits/stdc++.h>
using namespace std;

#define INF 0x3f3f3f3f
const int N = 100010;
struct BST
{
	int l,r,val,dat,cnt,size;
}a[N];
int idx,root,n;

void update(int p)
{
	a[p].size = a[a[p].l].size + a[a[p].r].size + a[p].cnt;
}

// 新增一个节点
int New(int v)
{	
	a[++idx].val = v;
	a[idx].dat = rand();//随机权值
	a[idx].cnt = a[idx].size = 1;//初始为 1
	return idx;
}
void build()
{
	New(-INF);New(INF);
	root = 1,a[1].r = 2;
	update(1);
}
void zig(int &p)
{ 
	int q = a[p].l;
	a[p].l = a[q].r,a[q].r = p,p = q; //p 是引用
	update(a[p].r);update(p); // 从下到上更新
}
void zag(int &p)
{
	int q = a[p].r;
	a[p].r = a[q].l,a[q].l = p,p = q;
	update(a[p].l);update(p);
}

int get_rank(int p,int val)
{
	if (p == 0) return 0;
	if (val == a[p].val) return a[a[p].l].size + 1;
	if (val < a[p].val) return get_rank(a[p].l,val); //往左查询
	return get_rank(a[p].r,val) + a[a[p].l].size + a[p].cnt; // 往右加上
}
int getval(int p,int rank)
{
	if (p == 0) return INF; // 没找到
	if (a[a[p].l].size >= rank) return getval(a[p].l,rank);
	if (a[a[p].l].size + a[p].cnt >= rank) return a[p].val;
	return getval(a[p].r,rank-a[a[p].l].size-a[p].cnt); //在右边
}
int find(int p,int val)
{
	if (p == 0) return 0;
	if (val == a[p].val) return p;
	if (val < a[p].val) return find(a[p].l,val);
	else return find(a[p].r,val);
}
void insert(int &p,int val)
{
	//找到则新增节点，由于是引用，所以其父节点会自动更新子节点的值
	if (p == 0) {p = New(val);return;} 
	if (val == a[p].val)
	{
		a[p].cnt++;//在树中
		update(p);//更新子树大小
		return;
	}
	if (val < a[p].val) //若小于则在左子树查询
	{
		insert(a[p].l,val);
		if (a[p].dat < a[a[p].l].dat) zig(p); //检查是否满足堆的性质
	}
	else 
	{
		insert(a[p].r,val);
		if (a[p].dat < a[a[p].r].dat) zag(p);
	}
	update(p);//插入完每次更新
}



int get_pre(int val)
{
	int ans = 1;//a[1].val = -INF
	int p = root;
	while (p)
	{
		if (val == a[p].val) 
		{
			if (a[p].l > 0) //有左子树
			{
				p = a[p].l;//返回左子树最右
				while (a[p].r > 0) p = a[p].r;
				ans = p;
			}
			break;//直接返回ans
		}
		if (a[p].val < val && a[p].val > a[ans].val) ans = p;
		if (val < a[p].val) p = a[p].l;
		else p = a[p].r;
	}
	return a[ans].val;
}
int get_next(int val)
{
	int ans = 2; // a[2].val = INF
	int p = root;
	while (p)
	{
		if (val == a[p].val) //检索val
		{
			if (a[p].r > 0) //有右子树
			{
				p = a[p].r;
				while (a[p].l) p = a[p].l;
				ans = p; 
			}
			break; //直接返回ans
		}
		if (a[p].val > val && a[p].val < a[ans].val) ans = p; //满足后继更新答案
		if  (val < a[p].val) p = a[p].l;
		else p = a[p].r;
	}
	return a[ans].val;
}

void remove(int &p,int val)
{
	if (p == 0) return;
	if (val == a[p].val) //找到节点后删除
	{
		if (a[p].cnt > 1) 
		{
			a[p].cnt--;
			update(p);
			return;
		}
		if (a[p].l || a[p].r) //有子树
		{
			//如果只有左子树或左子树随机值比较大，则让左节点作为父亲（右旋）
			if (a[p].r == 0 || a[a[p].l].dat > a[a[p].r].dat) zig(p),remove(a[p].r,val);
			else  zag(p),remove(a[p].l,val);  //递归删除
			update(p); 
		}
		else p = 0;
		return;
	}
	if (val < a[p].val) remove(a[p].l,val);
	else remove(a[p].r,val);
	update(p);
}
int main()
{
	build();
	cin >> n;
	while (n--)
	{
		int opt,x;
		cin >> opt >> x;
		if (opt == 1) insert(root,x);	
		else if (opt == 2) remove(root,x);
		else if (opt == 3) 
		{
			insert(root,x); //防止序列中没有x
			cout << get_rank(root,x) - 1 << endl;
			remove(root,x);
		}
		else if (opt == 4) cout << getval(root,x+1) << endl;
		else if (opt == 5) cout << get_pre(x) << endl;
		else cout << get_next(x) << endl;
	}
	return 0;
}

https://codeforces.com/contest/702/submission/330698498

posted @ 2024-01-03 23:00  codwarm  阅读(89)  评论(0)    收藏  举报