不确定性的表示

信念度

命题E：卫星上有电子异常

命题T：卫星上有推进器异常

命题C：出现了通讯故障

则在出现了通讯故障的情况下，相比”卫星上有推进器异常“，我们更相信”卫星上有电子异常“，即

\[(E|C)\succ(T|C) \]

在普适的可比性假设和传递性假设下，可以扩展为实值函数 \(P:P(E|C)>P(T|C)\)

假设P满足概率论公理，即\(0\le P(A|B)\le1\) :

1. 如果（A|B）是确定的，则P（A|B）=1；
2. 其他同理

概率

条件概率

\[P(A|B)=\frac{P(A,B)}{P(B)} \]

全概率法则

\[P(A|C)=\sum_{B\in\mathfrak{B}}P(A|B,C)P(B|C) \]

\[\begin{aligned} P(A|C)&=\sum_{B\in\mathfrak{B}}P(A,B|C)\\ &=\sum_{B\in\mathfrak{B}}\frac{P(A,B,C)}{P(C)}\\ &=\sum_{B\in\mathfrak{B}}\left(\frac{P(A,B,C)}{P(B,C)}\frac{P(B,C)}{P(C)}\right)\\ &=\sum_{B\in\mathfrak{B}}P(A|B,C)P(B|C) \end{aligned} \]

贝叶斯规则

\[P(A|B)=\frac{P(B|A)P(A)}{P(B)} \]

含有条件E的通用表达：

\[P(A|B,E)=\frac{P(B|A,E)P(A|E)}{P(B|E)} \]

应用贝叶斯规则

将位置因素cause造成的结果effect看作证据，确定未知因素cause：

\[P(cause|effect)=\frac{P(effect|cause)P(cause)}{P(effect)} \]

概率分布

1. 离散概率分布
2. 连续概率分布

连续概率分布

1. 均匀分布
2. 高斯分布

3. 截断式高斯分布

密度函数：

\[\mathcal{N}(w|\mu,\sigma^2,a,b)=\frac{\frac{1}{\sigma}\phi(\frac{w-\mu}{\sigma})}{\Phi(\frac{b-\mu}{\sigma})-\Phi(\frac{a-\mu}{\sigma})} \]

分母的作用即将区间限定为[a,b]并归一化

4. 多模态的连续概率分布

联合概率分布

离散联合分布

多个随机变量的概率分布，即表格

独立的参数个数的指数增长，带来了表示不确定性和学习概率模型的困难

独立性假设

变量X和Y是独立的，当且仅当 \(P(X，Y)=P(X)P(Y)\) ,记为 \(X\perp Y\)

决策树表示

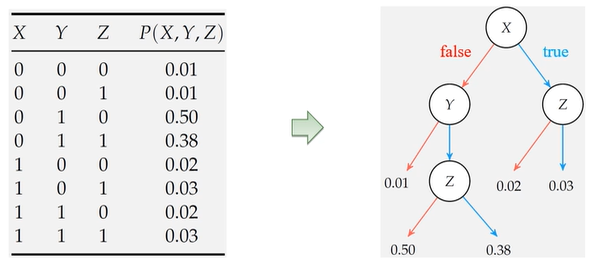
连续联合分布

多元均匀分布：

\[U(x|a,b)=\prod_{i=1}^nU(x_i|a_i,b_i) \]

多元均匀分布的混合模型：

\[p(x|a_1,b_1,\dots,a_k,b_k,\rho_1,\dots,\rho_k)=\sum_{j=1}^k\rho_jU(x|a_jb_j)\\ \sum_{j=1}^k\rho_j=1 \]

多元高斯分布：

\[\mathcal{N}(x|\mu,\Sigma)=\frac{1}{(2\pi)^{n/2}|\Sigma|^{1/2}}\mathrm{exp}\left(-\frac{1}{2}(x-\mu)^T\Sigma^{-1}(x-\mu)\right) \]

其中 \(x\in\mathbb{R}^n\) ,\(\mu\) 为均值向量， \(\Sigma\) 为协方差矩阵

条件概率模型

离散条件模型

连续条件模型

贝叶斯网络

贝叶斯网络是联合分布的一种紧凑表示

网络结构：有向无环图

1. 结点：随机变量
2. 有向边：联接节点对

贝叶斯网络中的条件独立关系：

给定Z，变量X和Y是独立的，当且仅当 \(P(X,Y|Z)=P(X|Z)P(Y|Z)\) ,记为 \((X\perp Y|Z)\)

贝叶斯网络中，节点仅条件依赖于其父节点

链式法则：\(P(X_i|P_{a_{X_i}})\) ：结点\(X_i\)的条件概率分布

时序模型

时序模型表示一组变量如何随时间演进

马尔科夫链

\(S_t\) 表示 \(t\) 时刻的状态

状态转移模型：条件分布 \(P(S_t|S_{t-1})\) 满足马尔可夫性质

马尔可夫性质：系统下一时刻的状态仅有当前状态决定，不依赖于以往的任何状态

隐马尔可夫模型

在马尔可夫链上增加观察节点