直线段的三种裁剪算法

 

一、Cohen-Sutherland

 

  

  

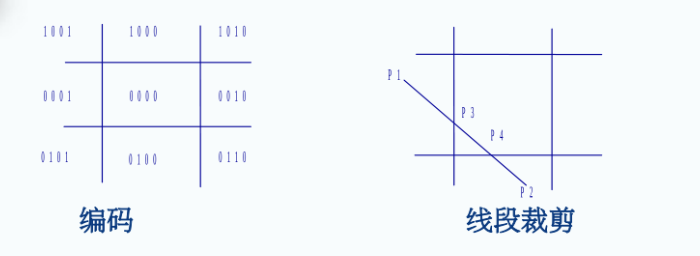
  （1）求出点 P1 和 P2 所在区域的区域代码 C1 和 C2

  （2）根据区域代码判断直线相对于窗口的位置：

      若C1 = C2 = 0，两个点在窗口内，应该予以保留。

      若C1 & C2 ≠ 0，两个点在同一侧，应该予以舍弃。

      若C1 & C2 = 0， 两个点不在同一侧，求出交点。

  （3）求交点

      将C1和C2分别与四条边对应的区域代码作&运算，当两者不为零时，说明该点与这条边有交点。然后根据直线方程和该边的坐标值求出交点。

 

  🔺缺点：求出的交点可能是直线的延长线上的点。

 

二、Liang-Barsky

  （1）两点的坐标值 X1，Y1， X2，Y2，窗口的坐标值 Xmin，Ymin，Xmax，Ymax，以及 △x 和 △y

  （2）求出Pk，Qk，Uk

    

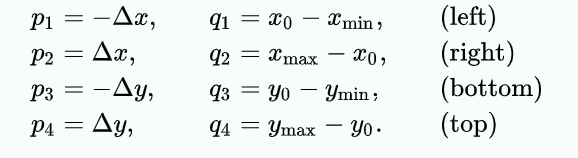
  （3）求出 t1，t2

  （4）若 t1 < t2，求出两点的坐标

    xx1 = x1 + t1*△x 

    xx2 = x1 + t2*△x 

    yy1 = y1 + t1*△y

    yy2 = y1 + t2*△y

 

             

 

 

参考资料链接：

  维基百科-liang-barsky

  使用伪代码解释 liang-barsky-line-clipping-algorithm

 

------------恢复内容开始------------

 

一、Cohen-Sutherland

 

  

  

  （1）求出点 P1 和 P2 所在区域的区域代码 C1 和 C2

  （2）根据区域代码判断直线相对于窗口的位置：

      若C1 = C2 = 0，两个点在窗口内，应该予以保留。

      若C1 & C2 ≠ 0，两个点在同一侧，应该予以舍弃。

      若C1 & C2 = 0， 两个点不在同一侧，求出交点。

  （3）求交点

      将C1和C2分别与四条边对应的区域代码作&运算，当两者不为零时，说明该点与这条边有交点。然后根据直线方程和该边的坐标值求出交点。

 

  🔺缺点：求出的交点可能是直线的延长线上的点。

 

二、Liang-Barsky

  （1）两点的坐标值 X1，Y1， X2，Y2，窗口的坐标值 Xmin，Ymin，Xmax，Ymax，以及 △x 和 △y

  （2）求出Pk，Qk，Uk

    

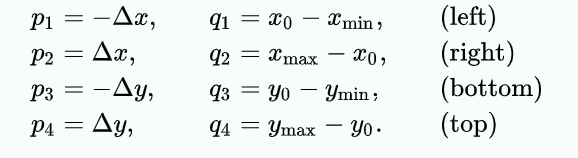
  （3）求出 t1，t2

  （4）若 t1 < t2，求出两点的坐标

    xx1 = x1 + t1*△x 

    xx2 = x1 + t2*△x 

    yy1 = y1 + t1*△y

    yy2 = y1 + t2*△y

 

             

 

 

参考资料链接：

  维基百科-liang-barsky

  使用伪代码解释 liang-barsky-line-clipping-algorithm

 

------------恢复内容结束------------