day23 | lc39组合总和 | lc40组合总和III | lc131分割回文串
day23
lc39_组合总和
给定一个无重复元素的数组 candidates 和一个目标数 target ,找出 candidates 中所有可以使数字和为 target 的组合。
candidates 中的数字可以无限制重复被选取。
说明:
- 所有数字(包括 target)都是正整数。
- 解集不能包含重复的组合。
示例 1:
- 输入:candidates = [2,3,6,7], target = 7,
- 所求解集为: [ [7], [2,2,3] ]
本题和lc77, lc216的区别是 本题没有数量要求 ,可以无限重复,但是有总和限制,所以间接来讲, 也是有个数限制
构造出来的二叉树结构为:
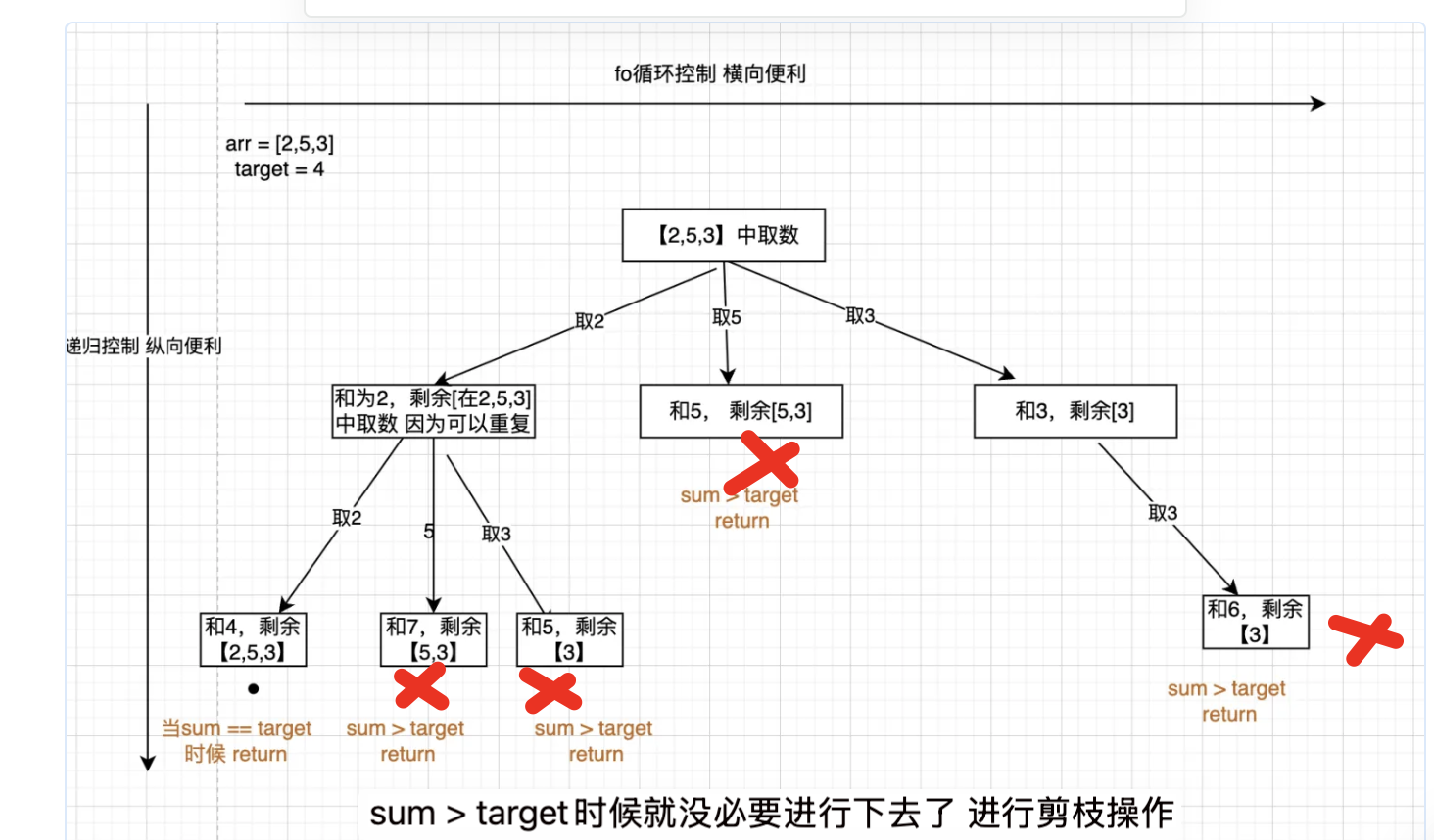
回溯三部曲
- 函数的参数和返回值
void backtracking
参数:
list集合的res 存放结果集
数组的path 存放符合条件的结果
int的sum 来统计单一结果path里面的总和
sIndex 用于控制for循环的起始位置
如果是一个集合来求组合 就需要sIndex 如果是多个集合取组合 各个集合不受影响就不需要
- 终止条件
当得出的总和大于 目标值 就返回 没必要执行下去了
当得出总和 == 目标 说明找到了符合条件的 返回结果
- 单层回溯条件
本题的单层for循环依旧sIndex开始 到arr的大小
注意可以重复 那就再调用递归时候 就不用i+1了
剪枝操作 i < arr.size() && sum + arr[i] <= target
在求和问题中,排序之后加剪枝是常见的套路!
public List<List<Integer>> combinationSum(int[] arr, int target){
List<List<Integer>> res = new ArrayList<>();
List<Integer> path = new ArrayList<>();
Arrays.sort(arr); // 先进行排序 便于后面剪枝
backtracking(arr,target,0,0,res,path);
return res;
}
private void backtracking(int[] arr, int target, int sum, int sIndex, List<List<Integer>> res, List<Integer> path) {
if(sum == target){
res.add(new ArrayList<>(path));
return;
}
for(int i = sIndex; i < arr.length; i++){
sum += arr[i];
if(sum > target) break;
path.add(arr[i]);
backtracking(arr,target,sum,i,res,path);
sum -= arr[i];
path.remove(path.size() - 1);
}
}
lc40_组合总和III
给定一个数组 candidates 和一个目标数 target ,找出 candidates 中所有可以使数字和为 target 的组合。
candidates 中的每个数字在每个组合中只能使用一次。
说明: 所有数字(包括目标数)都是正整数。解集不能包含重复的组合。
本题重点 : 1. 给定的集合(数组candidates)有重复元素,但结果集还不能有重复的组合。
** 2. **candidates 中的每个数字在每个组合中只能使用一次。
进行去重,所谓去重,其实就是使用过的元素不能重复选取
使用过的有两种 1.是同一树枝上使用过的
2, 同一树层使用过的 (需要先进行排序,目的相邻的两个在一起)
回看本题要求: 元素在同一组合内可以重复 但是两个组合不能相同 所以要去重的是同一树层
那么如何判断同一树层上元素(相同的元素)是否使用过了呢。
如果**<font style="color:rgb(71, 101, 130);">candidates[i] == candidates[i - 1]</font>** 并且 **<font style="color:rgb(71, 101, 130);">used[i - 1] == false</font>**,就说明:前一个树枝,使用了candidates[i - 1],也就是说同一树层使用过candidates[i - 1]。 此时for循环里就应该做continue的操作。
class Solution {
public List<List<Integer>> combinationSum2(int[] candidates, int target) {
List<List<Integer>> res = new ArrayList<>();
List<Integer> path = new ArrayList<>();
boolean[] used = new boolean[candidates.length]; // 是否使用过
Arrays.fill(used, false); // 初始化 快速填充used数组
Arrays.sort(candidates); // 对数组排序,方便去重
backtracking(candidates, target, 0, 0, res, path, used);
return res;
}
public void backtracking(int[] arr, int target, int sum, int startIndex,
List<List<Integer>> res, List<Integer> path, boolean[] used) {
// 如果找到一个组合,则添加到结果集中
if (sum == target) {
res.add(new ArrayList<>(path));
return; // 结束当前递归分支
}
for (int i = startIndex; i < arr.length; i++) {
// 剪枝操作:如果当前数字加起来超过 target,则无需继续
if (sum + arr[i] > target) break;
// 去重:跳过同层的重复元素
if (i > 0 && arr[i] == arr[i - 1] && !used[i - 1]) continue;
// 选择当前数字
used[i] = true;
sum += arr[i];
path.add(arr[i]);
// 递归到下一层,注意从下一个位置开始
backtracking(arr, target, sum, i + 1, res, path, used);
// 回溯:
used[i] = false;
sum -= arr[i];
path.remove(path.size() - 1);
}
}
}
本题也可以不借助used数组 仅仅使用startIndex来控制去重
class Solution {
public List<List<Integer>> combinationSum2(int[] candidates, int target) {
List<List<Integer>> res = new ArrayList<>();
List<Integer> path = new ArrayList<>();
int sum = 0;
// 排序,方便去重
Arrays.sort(candidates);
// 调用回溯函数
backTracking(candidates, target, 0, res, path, sum);
return res;
}
private void backTracking(int[] candidates, int target, int start,
List<List<Integer>> res, List<Integer> path, int sum) {
if (sum == target) {
// 如果路径的和等于目标值,保存当前路径
res.add(new ArrayList<>(path));
return;
}
for (int i = start; i < candidates.length && sum + candidates[i] <= target; i++) {
// 去重:跳过同一树层中相同的数字
if (i > start && candidates[i] == candidates[i - 1]) continue;
// 选择当前数字
sum += candidates[i];
path.add(candidates[i]);
// 递归,进入下一层,`i + 1` 表示当前数字只能用一次
backTracking(candidates, target, i + 1, res, path, sum);
// 回溯,撤销选择
sum -= candidates[i];
path.remove(path.size() - 1);
}
}
}
lc131_分割回文串
给定一个字符串 s,将 s 分割成一些子串,使每个子串都是回文串。
返回 s 所有可能的分割方案。
示例: 输入: "aab" 输出: [ ["aa","b"], ["a","a","b"] ]
回文串: 是向前和向后读都相同的字符串。�
分割的过程 和 回溯法的选取元素的过程类似 分割的区间组成了子串
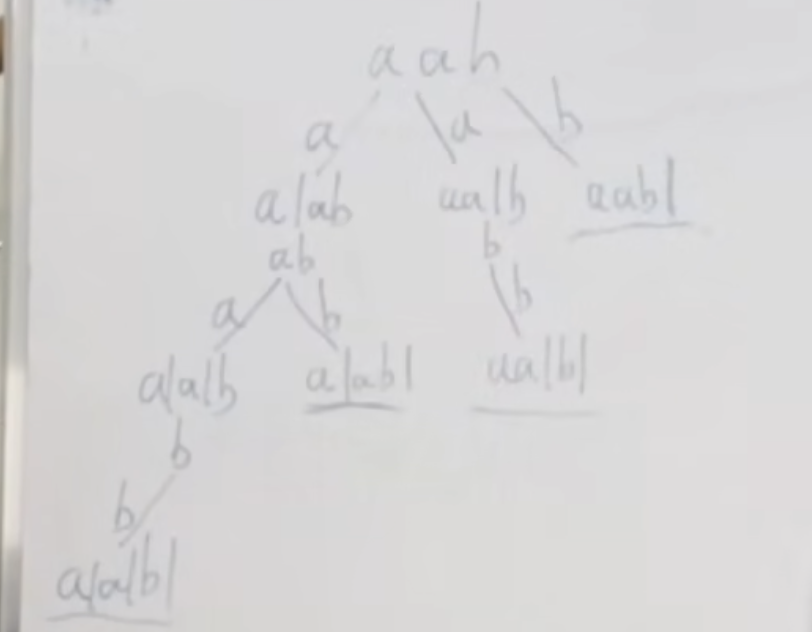
子串的范围: (startIndex, i] 因为sIndex是固定的 但是i是不断的加加的 所以表示范围
几个难点:
- 切割问题可以抽象为组合问题
- 如何模拟切割线
startIndex就是切割线
- 切割问题中递归如何终止
切割线切到了字符串最后面,说明找到了一种切割方法,此时就是本层递归的终止条件。
- 在递归循环中如何截取子串
在<font style="color:rgb(71, 101, 130);">for (int i = startIndex; i < s.size(); i++)</font>循环中,我们 定义了起始位置startIndex,那么 [startIndex, i] 就是要截取的子串。
首先判断这个子串是不是回文,如果是回文,就加入<font style="color:rgb(71, 101, 130);">path</font>中,path用来记录切割过的回文子串。
- 如何判断回文
判断是否为回文子串: 使用双指针法,一个指针从前向后,一个指针从后向前,如果前后指针所指向的元素是相等的,就是回文字符串了。
public List<List<String>> partition(String s) {
List<List<String>> res = new ArrayList<>();
List<String> path = new ArrayList<>();
backtracking(s, path, res, 0);
return res;
}
private void backtracking(String s, List<String> path, List<List<String>> res, int sIndex) {
if(sIndex == s.length()){
res.add(new ArrayList<>(path));
return;
}
StringBuilder sb = new StringBuilder(); // 用于判断是否回文
for(int i = sIndex; i < s.length(); i++){
sb.append(s.charAt(i));
if(check(sb)){ // 如果是回文 就收集起来
path.add(sb.toString());
backtracking(s, path, res, i + 1);
path.remove(path.size() - 1);
}
}
}
// 双指针判断是否为回文子串
public boolean check(StringBuilder sb){
for(int i = 0; i < sb.length(); i++){
if(sb.charAt(i) != sb.charAt(sb.length() - 1 - i)) return false;
}
return true;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号