代码随想录-算法训练day1-day12
day1(10.30)
数组基础部分
重点:: 数组的元素是不能删的,只能被覆盖。
题目
lc704二分查找
- 把握条件
到底是小于 还是小于等于 怎么决定?
关键在于明确区间的定义 到底是[l, r) ** 还是[l ,r ]**
写法一: [ ]
public int search(int[] nums, int target) {
if (target < nums[0] || target > nums[nums.length - 1]) return -1;
int l = 0, r = nums.length - 1;
while(l <= r){
int mid = l + ((r - l)>>1);
if(nums[mid] == target) return mid;
else if(nums[mid] > target) r = mid + 1;
else l = mid - 1;
}
return -1;
}
写法二: [ )
public int search(int[] nums, int target) {
if (target < nums[0] || target > nums[nums.length - 1]) return -1;
int l = 0, r = nums.length;
while(l < r){
int mid = l + ((r - l) >>1);
if(nums[mid] == target) return mid;
else if(nums[mid] > target) r = m;
else l = m + 1;
}
return -1;
}
lc27移除元素
使用快慢指针 目的是使用一层for 来干原本两个for的事
fast快指针代表 寻找新数组需要的元素 也就是出了要删除的元素之外的所有其他元素
slow慢指针代表 新数组的下标
这样快指针获取到的值 赋给慢指针就行
当快指针指向的元素不等于要删除的 就是新数组所需要的
public int removeElement(int[] nums, int val) {
int s = 0;
for(int f = 0; f < nums.length; f++){
if(nums[f] != val){
nums[s] = nums[f];
s++;
}
}
return s;
}
lc977 有序数组的平方
一个有序数组 也有负数 比如
-5 1 2 3
给他开平方之后返回小到大的排列
因为含有负数 所以开平方之后 最大的元素一定分布在两边
循环条件 只要i <= j的时候就一直继续
public int[] sortedSquares(int[] nums) {
int l = 0, r = nums.length - 1, k = nums.length - 1;
wwhile(l <= r){
if(nums[l] * nums[l] > nums[r] * nums[r]){
res[k] = nums[l] * nums[l];
k--;
l++;
}else{
res[k] = nums[r] * nums[r];
k--;
r--;
}
}
return res;
}
注意:
l 是数组左边界 r 是有边界 j 是结果集数组的下标 设置为原本数组的右边届 往左走<--
左右边界对应的数平方 谁大就取谁
取到左边时候 左边要向右走 指针++
取到右边时候 右边届要想左走 指针--
day2
lc209 长度最小的子数组
给定一个含有 n 个正整数的数组和一个正整数 s ,找出该数组中满足其和 ≥ s 的长度最小的 连续 子数组,并返回其长度。如果不存在符合条件的子数组,返回 0。
示例:
- 输入:s = 7, nums = [2,3,1,2,4,3]
- 输出:2
- 解释:子数组 [4,3] 是该条件下的长度最小的子数组。
暴力解法:
两个for循环, 不断地找符合条件的子数组,但是时间复杂度是O(n^2) 但是在最后leetcode跟新了数据 这种很明显超时了.
滑动窗口(双指针):
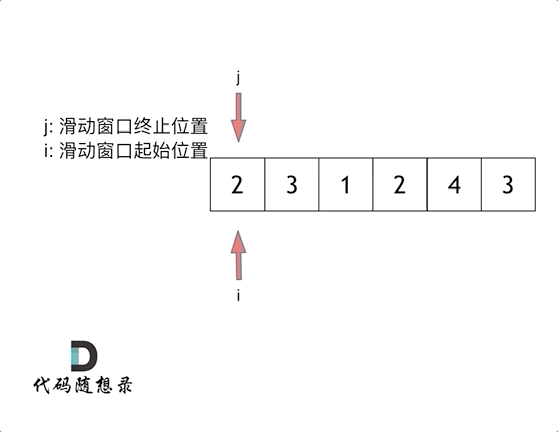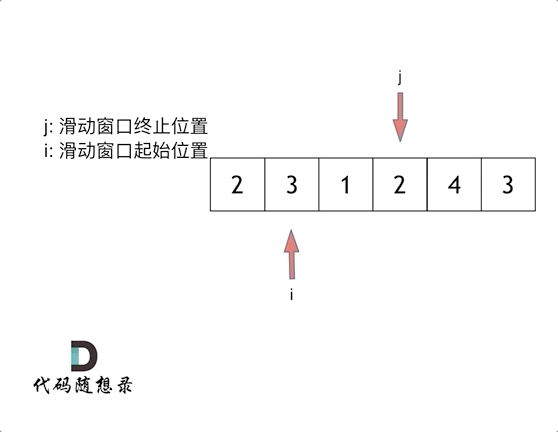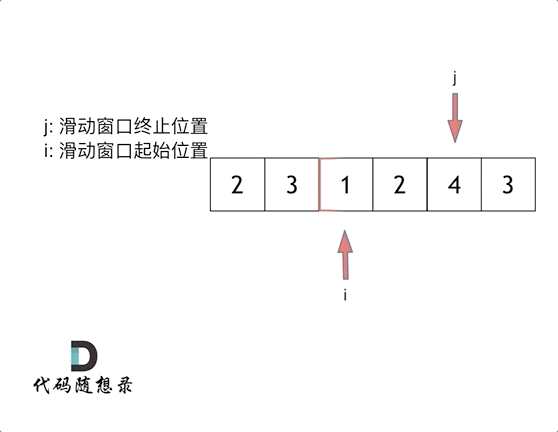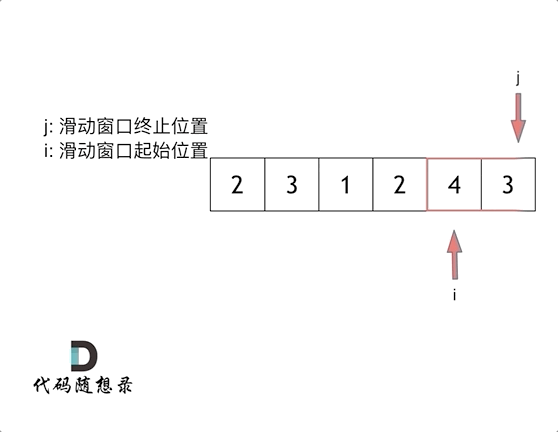
滑动窗口就是不断的调整子序列的起点和终点 直到得出想要的结果
俩指针
i 起点 j 终点 起点和终点最开始都在数组的第一个元素位置
先固定i 移动j 直到找到满足sum 满足了 就停止j终点
此时移动i起点 找到最短满足的 如果出现小于目标值的情况 那么固定i j继续移动
public int minSubArrayLen(int s, int[] nums){
int l = 0, sum = 0, res = Integer.MAX_VALUE;
for(int r = 0; r < nums.length; r++){
sum += nums[r];
while(sum >= s){
res = Math.min(res, r - l + 1);
sum -= nums[l++];
}
}
return res == Integer.MAX_VALUE ? 0 : res;
}
lc59螺旋矩阵I
给你一个正整数
<font style="color:rgba(38, 38, 38, 0.75);background-color:rgb(240, 240, 240);">n</font>,生成一个包含<font style="color:rgba(38, 38, 38, 0.75);background-color:rgb(240, 240, 240);">1</font>到<font style="color:rgba(38, 38, 38, 0.75);background-color:rgb(240, 240, 240);">n</font><sup><font style="color:rgba(38, 38, 38, 0.75);background-color:rgb(240, 240, 240);">2</font></sup>所有元素,且元素按顺时针顺序螺旋排列的<font style="color:rgba(38, 38, 38, 0.75);background-color:rgb(240, 240, 240);">n x n</font>正方形矩阵<font style="color:rgba(38, 38, 38, 0.75);background-color:rgb(240, 240, 240);">matrix</font>。
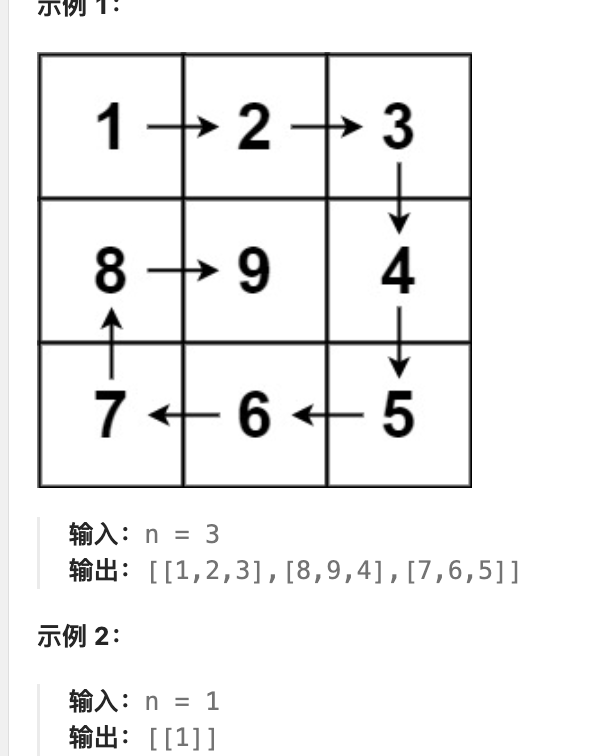
本题关键在于边界条件的处理 也就是四方形的四个角怎么处理
遵循一个不变量 到底是[ ] 还是[ )
如果[ ) 也就是在便利一条边时候 只要边的起点 不要边的终点 作为下一条的起点
题目输入n n就是 代表矩阵的大小 比如n = 4 那就返回4*4的矩阵
那么螺旋转圈次数就是n / 2次
如果n是奇数 除以2 除不尽剩余一个
因为每一圈的 起点都不算固定的 所以for循环的i 不可能是固定
public static int[][] generateMatrix(int n) {
int[][] arr = new int[n][n];
int startX = 0, startY = 0, offset = 1,loop = 1,count = 1,x,y;
while (loop <= n / 2){
for(y = startY; y < n - offset; y++) arr[startX][y] = count++;
for(x = startX; x < n - offset; x++) arr[x][y] = count++;
for( ; y > startY; y--) arr[x][y] = count++;
for( ; x > startX; x--) arr[x][y] = count++;
startX++;
startY++;
loop++;
offset++;
}
if(n % 2 == 1) arr[startX][startY] = count;
return arr;
}
前缀和
题目描述
给定一个整数数组 Array,请计算该数组在每个指定区间内元素的总和。
输入描述
第一行输入为整数数组 Array 的长度 n,接下来 n 行,每行一个整数,表示数组的元素。随后的输入为需要计算总和的区间,直至文件结束。
输出描述
输出每个指定区间内元素的总和。
思路:
- 暴力解法
有一个区间之后 直接暴力把这个区间的和都累加一遍 但是提交代码提示超时
- 前缀和
前缀和就是利用计算过的子数组的和 从而降低区间查询需要累加计算的次数
在设计计算区间和时候非常有用
比如要计算vec[i] 在这个数组上的区间和
首先累加 p[i]表示下标0~i的vec累加和
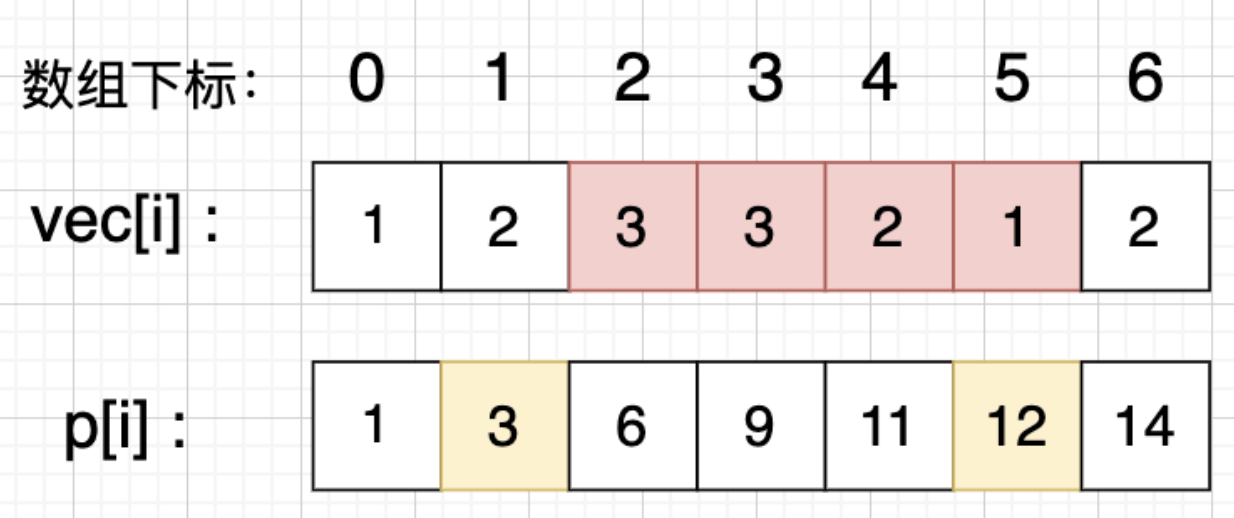
计算下标2到5的区间和
区间下标 [2, 5] 的区间和,那么应该是 p[5] - p[1],而不是 p[5] - p[2]。
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
int[] vec = new int[n]; //原本数组
int[] p = new int[n]; //原本数组的区间和
// 计算原本数组的区间和
int preSum = 0;
for(int i = 0; i < n; i++){
vec[i] = sc.nextInt();
preSum += vec[i];
p[i] = preSum;
}
while (sc.hasNextInt()){
int a = sc.nextInt();
int b = sc.nextInt();
int sum = 0;
if(a == 0) sum = p[b];
else sum = p[b] - p[a - 1];
System.out.println(sum);
}
}
}
开发商买土地
【题目描述】
在一个城市区域内,被划分成了n * m个连续的区块,每个区块都拥有不同的权值,代表着其土地价值。目前,有两家开发公司,A 公司和 B 公司,希望购买这个城市区域的土地。
现在,需要将这个城市区域的所有区块分配给 A 公司和 B 公司。
然而,由于城市规划的限制,只允许将区域按横向或纵向划分成两个子区域,而且每个子区域都必须包含一个或多个区块。
为了确保公平竞争,你需要找到一种分配方式,使得 A 公司和 B 公司各自的子区域内的土地总价值之差最小。
注意:区块不可再分。
解法思路:
本题 要求任意两行或者两列之间的数值之和, 也就是前缀和
先计算出行 列方向的和 然后统计好前n行的和 q[n] 如果要求a行到b行之间的总和 那么就是q[b] - q[a - 1]
将一个二维数组划分为两部分,使得这两部分的和之差最小。
首先计算整个数组的总和 sum,然后分别求出每一行和每一列的和,存储在 horizontal 和 vertical 数组中。
接着,通过累加 horizontal 数组中的行和,逐步模拟横向划分,将前几行作为一部分、剩余行作为另一部分。每次划分时,计算当前划分后两部分和的差值,并更新最小差值 result。同理,对于纵向划分,累加 vertical 数组中的列和,模拟不同的列划分方式,计算两部分的差值,并更新最小差值。最终输出的 result 就是所有可能划分方式中两部分和的最小差值。
import java.util.*;
public class Main{
public static void main (String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
int m = sc.nextInt();
int sum = 0;
int[][] vec = new int[n][m];
for(int i = 0; i < n; i++){
for(int j = 0; j < m; j++){
vec[i][j] = sc.nextInt();
sum += vec[i][j];
}
}
// 统计每行的和
int[] rowSum = new int[n];
for(int i = 0; i < n; i++){
for(int j = 0; j < m; j++){
rowSum[i] += vec[i][j];
}
}
// 统计每列的和
int[] colSum = new int[m];
for(int j = 0; j < m; j++){
for(int i = 0; i < n; i++){
colSum[j] += vec[i][j];
}
}
int res = Integer.MAX_VALUE;
// 计算行划分的最小差值
int rowCut = 0;
for(int i = 0; i < n; i++){
rowCut += rowSum[i];
res = Math.min(res, Math.abs(sum - 2 * rowCut));
}
// 计算列划分的最小差值
int colCut = 0;
for(int j = 0; j < m; j++){
colCut += colSum[j];
res = Math.min(res, Math.abs(sum - 2 * colCut));
}
System.out.println(res);
sc.close();
}
}
day3 链表章节
链表基础部分
链表就是通过指针串联在一起的线性结构, 每个节点有两部分组成 分别是数据域 指针域 并且最后一个指针指向null
单链表中的指针只能指向节点的下一个
双链表: 每个节点有两个指针 一个指针指向下一个节点 一个指向上一个节点
循环链表: 首尾相连
定义节点:
public class Node{
int v;
Node next;
}
删除节点:
比如a --> b ---> c ----> d ---> null 如果要删除的b节点 那么
只需要将b节点的next指针指向d即可, c节点会被gc回收
添加节点:
在b c中间添加个f 也就是 将b指针指向f f指针指向c
总结:
链表的增加和删除都是O1操作,也不会影响到另一个节点
lc203 移除链表元素
题意:删除链表中等于给定值 val 的所有节点。
示例 1: 输入:head = [1,2,6,3,4,5,6], val = 6 输出:[1,2,3,4,5]
示例 2: 输入:head = [], val = 1 输出:[]
示例 3: 输入:head = [7,7,7,7], val = 7 输出:[]
本题删除链表中的元素
也就是让被删除的前一个节点 指向节点的下一个节点就可以了
但是 如果被删除的节点恰好就是头结点呢? 头节点本身就是第一个节点 不存在前一个节点
所以可以使用虚拟节点法 重新定义一个虚拟临时节点 指向头结点
如果删除的是头结点 那么就可以让临时节点直接指向头结点是下一个节点 最后return 是temp.next
public Node removeElements(Node head, int val) {
// 1. 设置虚拟节点
Node temp = new Node();
temp.next = head;
// 2. 当前指针
Node cur = temp;
// 便利
while(cur.next != null){
if(cur.next.val == val) cur.next = cur.next.next;
else cur = cur.next;
}
return temp.next;
}
lc707 设计链表
- get(index):获取链表中第 index 个节点的值。如果索引无效,则返回-1。
- addAtHead(val):在链表的第一个元素之前添加一个值为 val 的节点。插入后,新节点将成为链表的第一个节点。
- addAtTail(val):将值为 val 的节点追加到链表的最后一个元素。
- addAtIndex(index,val):在链表中的第 index 个节点之前添加值为 val 的节点。如果 index 等于链表的长度,则该节点将附加到链表的末尾。如果 index 大于链表长度,则不会插入节点。如果index小于0,则在头部插入节点。
- deleteAtIndex(index):如果索引 index 有效,则删除链表中的第 index 个节点。
这个题涵盖了链表的基本操作
头插 尾插 获取第n个值 第n个节点前插 删除第n个
本题的初始化
class ListNode {
int val;
ListNode next;
ListNode(){}
ListNode(int val) {
this.val=val;
}
}
-----
class MyLinkedList {
//size存储链表元素的个数
int size;
//虚拟头结点
ListNode head;
//初始化链表
public MyLinkedList() {
size = 0;
head = new ListNode(0);
}
........
........
}
- 获取第n个值
public int get(int index){
if(index < 0 || index >= size) return -1;
Node cur = head;
for(int i = 0; i <= index; i++) cur = cur.next;
return cur.val;
}
- 头插
// 头插等价于在第0个元素前添加
public void addAtHead(int val){
Node newNode = new Node(val);
newNode.next = head.next;
head.next = newNode;
size++;
}
- 尾插
// 尾差等价于在(末尾+1)个元素前面添加
public void addAtTail(int val){
Node newNode = new Node(val);
Node cur = head;
while(cur.next != null) cur = cur.next;
cur.next = newNode;
size++;
}
- 在第n个节点前面插入
// 如果index大于链表的总长度 返回空
// 如果index等于链表的长度 就说明是新插入节点的尾巴节点
// 第index节点之前插入一个新节点 假如index = 0, 那就代表新插入的节点是链表的新头结点
public void addAtIndex(int index, int val){
if(index > size) return;
if(index < 0) index = 0;
size++;
// 找到要插入节点的前一个节点
Node pred = head;
for(int i = 0; i < index; i++) pred = pred.next;
Node toAdd = new Node(val);
toAdd.next = pred.next;
pred.next = toAdd;
}
- 删除第n个节点
public void delAtIndex(int index){
if(index < 0 || index >= size) return;
size--;
Node pred = head;
for(int i = 0; i < index; i++) pred = pred.next;
pred.next = pred.next.next;
}
lc206翻转单链表
示例: 输入: 1->2->3->4->5->NULL 输出: 5->4->3->2->1->NULL
写法一: 双指针解法
首先 定义了三个节点变量
pre当前节点的前一个节点 初始化为null 因为翻转之后的链表的尾巴节点应该指向null
cur当前节点 初始化为头结点
temp 临时节点 用于暂存cur的下一个节点 避免翻转的时候丢失链表的后续节点
翻转过程
- 保存cur.next 到temp
- 将cur.next设置为pre 翻转当前节点的指针
- 将pre更新为cur 前一个节点就是现在的节点
- cur设置为temp 向链表的下一个节点移动
- 返回新头结点 pre指向原本链表的最后一个节点 这个节点也就是翻转过后的新头结点
public Node reverseList(Node head){
Node pre = null, cur = head, temp = null;
while(cur != null){
temp = cur.next;
cur.next = pre;
pre = cur;
cur = temp;
}
return pre;
}
写法二: 递归
public Node reverseList(Node head){
return reverse(null, head);
}
private Node reverse(Node pre, Node cur){
if(cur == null) return pre;
Node temp = null;
temp = cur.next;
cur.next = pre; // 翻转
return reverse(cur, temp);
}
day4
lc19 删除倒数第k个节点
本题的关键在于怎么找到倒数第k个节点呢?
使用快慢指针, f快指针先移动k+1步,让f和s相差k个节点, 然后快慢同时走,直到快指针到尾巴,此时慢指针就是倒数第k个节点
public static Node removeNthFromEnd(Node head, int n) {
// 1. 虚拟头结点 创建双指针
Node temp = new Node(-1);
temp.next = head;
Node f = temp, s = temp;
// 2. 快指针走k+1
for(int i = 0; i <= n; i++) f = f.next;
// 3. f s同时走
while(f != null){
f = f.next;
s = s.next;
}
// 4. 删除s指向 的节点 并返回
if(s.next != null) s.next = s.next.next;
return temp.next
}
链表相交
本题关键在于:
**设置双指针 当两个指针遍历完自己的链表之后,在切换到对方的链表继续遍历。只要相遇,那一定是在交点相遇。如果没有交点,那就在
**null**相遇。
**
public Node getIntersectionNode(Node headA,Node headB){
Node indexA = headA, indexB = headB;
while(indexA != indexB){
if(indexA == null) indexA = headB;
else indexA = indexA.next;
if(indexB == null) indexB = headA;
else indexB = indexB.next;
}
return indexA;
}
lc142. 环形链表II
本题包含两部分
- 判断是否有环
通过快慢指针 但凡相遇 那一定有环
- 找到环的入口
有环之后 定义两个指针 一个指向快或者慢指针 一个指向头结点 开始同步移动 当两个相等相遇的地方 一定是环的入口
public Node detectCycle(Node head) {
Node f = head, s = head;
while(f != null && f.next != null){
f = f.next.next;
s = s.next;
if(f == s){
Node index1 = f, index2 = head;
while(index1 != index2){
index1 = index1.next;
index2 = index2.next;
}
return index1;
}
}
return null;
}
lc24 两两交换链表中的节点
本题依旧采用虚拟头结点方式
修改这个节点的指向 必须找到这个节点的前一个节点指针
改变指针的走向实现交换 并不是交换数值
-
虚拟头结点
-
定义 cur 变量并初始化为 dumpHead,用于遍历链表,控制节点交换。
定义辅助变量 :
temp: 临时节点,保存两个节点后面的节点
firstNode、保存两个节点之中的第一个节点
secondNode,保存两个节点之中的第二个节点
- while循环 条件是是
cur.next和cur.next.next不为null
其中cur.next 和 cur.next.next 代表一对要交换的节点,如果不足一对(即只剩下一个节点或没有节点),则循环结束。
- 交换
temp 保存第二个节点的下一个节点,
firstNode 指向当前要交换的第一个节点,secondNode 指向当前要交换的第二个节点。
开始交换.....
cur.next = secondNode:将cur的下一个节点指向secondNode,完成第一步交换。secondNode.next = firstNode:将secondNode的下一个节点指向firstNode,完成第二步交换。firstNode.next = temp:将firstNode的下一个节点指向temp(即下一对的第一个节点)。cur = firstNode:将cur移动到firstNode,准备开始下一轮交换。
public Node swapPairs(Node head) {
Node dumpHead = new Node(-1);
dumpHead.next = head;
Node cur = dumpHead, temp, firstNode, secondNode;
while(cur.next != null && cur.next.next != null){
temp = cur.next.next.next;
firstNode = cur.next;
secondNode = cur.next.next;
cur.next = secondNode;
secondNode.next = firstNode
firstNode.next = temp;
cur = firstNode;
}
return dumpHead.next;
}
day06哈希表
总结的来说,当我们遇到了要快速判断一个元素是否出现集合里的时候,就要考虑哈希法。
但是哈希法也是牺牲了空间换取了时间,因为我们要使用额外的数组,set或者是map来存放数据,才能实现快速的查找。
lc242有效的字母异位词
给定两个字符串 s 和 t ,编写一个函数来判断 t 是否是 s 的字母异位词。
示例 1: 输入: s = "anagram", t = "nagaram" 输出: true
示例 2: 输入: s = "rat", t = "car" 输出: false
说明: 你可以假设字符串只包含小写字母。
读题可以看不懂到底什么是字母异位词呢?
大白话就是 给定两个字符串 判断是否有相同的字母组成(不管顺序)
比如 abbc --- bbac 这这就是一对字母异位词
因为知道这些字母只能是小写字母 而且字母的asc码都是连续的
所以可以定一个数组 大小是26 刚好能放入26个字母 用来记录字符串s里字符出现的次数。
因为asc码都是连续的 所以a到z是26个连续的数 所以将(s[i] - 'a')++ 求出来一个数字
同样,在便利t的时候,只需要-- 就可以了
其实也就是26个字母对应26个下标 出现一次就对应下标加一 出现的位置比如
t='abcdef.....z' 26个 那么依次加加操作之后就是 arr[1,1,1,1,1,1,1,1,1,1,1,1,......1] 26个1
最后检查这个数组,如果有元素不等于0 说明s或者t字符串一定有一个多了 或者少了
如果都是等于0 说明就是字母异位词
时间复杂度为O(n),空间上因为定义是的一个常量大小的辅助数组,所以空间复杂度为O(1)。
--------
也就是:
第一次便利s的时候 遇到每个字母就把他在数组对应的位置加1 表示出现过
第二次便利t的时候 遇到的时候 就把对应位置减1
如果最后结果数组都是0 代表两个字符串完全相等
public boolean isAnagram(String s, String t) {
int[] arr = new int[26];
for(int i = 0; i < s.length(); i++) arr[s.charAt(i) - 'a']++;
for(int i = 0; i < t.length(); i++) arr[t.chatAt(i) - 'a']--;
for(int c : arr){
if(c != 0) return false;
}
return true;
}
lc349两个数组的交集
> 题意:给定两个数组,编写一个函数来计算它们的交集。 > > 输入:nums1 = [4,9,5],nums2 = [9,4,9,8,4] > > 输出:[9,4] >使用set结构 定义 s1 res
s1 用于存放num1中的元素也就是 s1 = {4,9,5}
res 用于nums1和nums2经过去重之后交集部分
执行结果:
nums2[0] = 9,s1包含9,添加到res:res = {9}nums2[1] = 4,s1包含4,添加到res:res = {9, 4}nums2[2] = 9,res已经包含9,所以不重复添加。nums2[3] = 8,s1不包含8,跳过。nums2[4] = 4,res已经包含4,所以不重复添加。
最终,res = {9, 4},这是 nums1 和 nums2 的交集。
public int[] intersection(int[] nums1, int[] nums2) {
if (nums1 == null || nums1.length == 0 || nums2 == null || nums2.length == 0) return new int[0];
// 初始化set
Set<Integer> s1 = new HashSet<>();
Set<Integer> res = new HashSet<>();
//便利num1
for(int i : nums1) s1.add(i);
// 便利num2时候需要先去重
for(int i : nums2){
if(s1.contains(i)) res.add(i);
}
//申请新数组存放结果 并且返回
int[] arr = new int[res.size()];
int index = 0;
for(int num : res) arr[index++] = num;
return arr;
}
lc202 快乐数
「快乐数」定义为:对于一个正整数,每一次将该数替换为它每个位置上的数字的平方和,然后重复这个过程直到这个数变为 1,也可能是 无限循环 但始终变不到 1。如果 可以变为 1,那么这个数就是快乐数。
编写一个算法来判断一个数 <font style="color:rgba(38, 38, 38, 0.75);background-color:rgb(240, 240, 240);">n</font> 是不是快乐数。
题目中说了会 无限循环,那么也就是说求和的过程中,sum会重复出现
这道题目使用哈希法,来判断这个sum是否重复出现,如果重复了就是return false, 否则一直找到sum为1为止。
public boolean isHappy(int n) {
Set<Integer> set = new HashSet<>();
while(n != 1 && set.contains(n)){
set.add(n);
n = getNumber(n);
}
return n == 1;
}
public int getNumber(int n) {
int res = 0;
while(n > 0){
int temp = n % 10 //取出个位
res += temp * temp;
n /= 10;
}
return res;
}
lc1 两数之和
梦的开始!!!!!
使用map来记录数字和下标
map中的存储结构为 {key:数据元素,value:数组元素对应的下标}。
public int[] twoSum(int[] nums. int target){
int[] res = new int[2];
if(nums == null || nums.length ==0) return res;
Map<Integer, Integer> map = new HashMap<>();
for(int i = 0; i < nums.length; i++){
int temp = target - nums[i];
if(map.containsKey(temp)){
res[1] = i;
res[0] = map.get(temp);
break;
}
map.put(nums[i], i);
}
return res;
}
day7
lc383 救赎信
和 242.有效的字母异位词 是一个思路 ,算是拓展题
lc383是求字符串a能否组成字符串b,而不用管字符串b 能不能组成字符串a
通过题意得出 1. magazines里面元素不能重复使用 2. 只有小写
public boolean canConstruct(String ransomNote, String magazine){
if(ransomNote.length() > magazine.length()) return false;
int[] res = new int[26];
for(char c : magazine.toCharArray()) res[c - 'a']++;
for(char c : ransomNote.toCharArray()) res[c - 'a']--;
for(int i : res){
if(i < 0) return false;
}
return true;
}
lc454 四数相加II
给你四个整数数组 nums1、nums2、nums3 和 nums4 ,数组长度都是 n ,� 请你计算有多少个元组 (i, j, k, l) 能满足:�
- 0 <= i, j, k, l < n�
- nums1[i] + nums2[j] + nums3[k] + nums4[l] == 0�
给你4个数组 在这4个数组分别找出一个元素 使得这几个元素相加等于0 问你一共多少对符合条件的(不要求分别是多少 只要有多少个符合要求)
因为是在4个数组里面 分别找一个 所以不用考虑去重
解法一: 暴力
暴力法: 4个for循环去便利4个数组 然后相加等于0的话 就++; 最后返回cout
但是时间复杂度是n的4次方
解法二: 使用HashMap 不仅要统计元素 还要统计次数
把4个数组分成两组,前两个数组 元素为a+b 放入map的key 同时统计a+b出现的次数
然后便利cd数组时候 去判断0-(c+d)有没有出现过 统计出现过的次数 然后count加value的值
为什么分成两组?
因为两个for循环时间复杂度是n的平方 另外一组的两个for也是n的平方 所以整体时间复杂度就是n的平方 因为时间复杂度是不管常数项的
为什么是 0-(c+d)?
如果0-(c+d) = a + b ----> 那么就是 a+b+c+d = 0
public int fourSumCount(int[] nums1, int[] nums2, int[] nums3, int[] nums4) {
Map<Integer, Integer> map = new HashMap<>();
int res = 0;
// 统计前两个数组中的元素之和并且统计次数
// 如果sum存在map 返回 对应值(出现次数) 不在就默认返回0
for(int i : nums1){
for(int j : nums2){
int sum = i + j;
map.put(sum, map.getOrDefault(sum, 0) + 1);
}
}
// 统计后俩
for(int i : nums3){
for (int j : nums4){
res += map.getOrDefault(0 - i - j, 0);
}
}
return res;
}
lc15 三数之和
** **给你一个包含 n 个整数的数组 nums,判断 nums 中是否存在三个元素 a,b,c ,使得 a + b + c = 0 ?请你找出所有满足条件且不重复的三元组。
注意 : 一个数组里面 去重
因为需要对ABC都要进行去重操作 所以属于双指针更加方便
先进行排序 然后三个指针 i l r i定于在数组开头 l在i+1位置 r在尾巴
也就转换成arr[i]+arr[l]+arr[r] = 0 接下来就是移动指针的操作了
如果三个相加大于0 那么l向后移动 直到l和r相遇
但是要对abc去重 也就是arr[i] arr[l] arr[r] 进行去重操作
如果a重复了 因为所以应该跳过去
还有一个问题就是判断arr[i] 和 arr[i + 1] 还是判断 arr[i - 1] 和 arr[i]呢?
如果是判断i+1进行去重的话 就把三元组结果集里面的重复数据去除了 比如{-1,-1,2}
我们要做的是 不能有重复的三元组,但结果集内的元素是可以重复的!
if (i > 0 && nums[i] == nums[i - 1]) continue;
那么b和c怎么去重呢?
其实这个去重应该放在找到一个结果集之后再进行去重
while (right > left && nums[right] == nums[right - 1]) right--;
while (right > left && nums[left] == nums[left + 1]) left++;
整体代码
public List<List<Integer>> threeSum(int[] nums) {
Arrays.sort(nums);
List<List<Integer>> res = new ArrayList<>();
for (int i = 0; i < nums.length; i++) {
if (nums[i] > 0) break; // 如果当前数大于0,则直接结束循环
if (i > 0 && nums[i] == nums[i - 1]) continue; // 去重
int l = i + 1, r = nums.length - 1; // 每次for循环都重新初始化l和r
while (l < r) {
int sum = nums[i] + nums[l] + nums[r];
if (sum > 0) r--;
else if (sum < 0) l++;
else {
res.add(Arrays.asList(nums[i], nums[l], nums[r]));
// 去重处理
while (l < r && nums[r] == nums[r - 1]) r--;
while (l < r && nums[l] == nums[l + 1]) l++;
r--;
l++;
}
}
}
return res;
}
lc18 四数之和
思路和三数之和差不多 就是多套了一层for
三数之和是三个指针 那么四数就是4个指针 关键点是target可以是负数 两个负数相加是可以变得更小的 所以在去重的时候要加大于0的条件
四数之和的双指针解法是两层for循环nums[k] + nums[i]为确定值,依然是循环内有left和right下标作为双指针,找出nums[k] + nums[i] + nums[left] + nums[right] == target的情况,三数之和的时间复杂度是O(n2),四数之和的时间复杂度是O(n3) 。
public List<List<Integer>> fourSum(int[] nums, int target) {
// 排序数组
Arrays.sort(nums);
List<List<Integer>> res = new ArrayList<>();
for(int k = 0; k < nums.length; k++){
// 剪枝
if(nums[k] > target && nums[k] > 0) break;
//去重
if(k > 0 && nums[k] == nums[k - 1]) continue;
for(int i = k + 1; i < nums.length; i++){
// 剪枝 去重i
if(nums[k] + nums[i] > target && nums[k] + nums[i] >= 0) break;
if(i > k + 1 && nums[i] == nums[i - 1]) continue;
// l 和 r
int l = i + 1, r = nums.length - 1;
while (l < r){
long sum = nums[k] + nums[i] + nums[l] + nums[r];
if(sum > target) r--;
else if (sum < target) l++;
else {
res.add(Arrays.asList(nums[k],nums[i],nums[l],nums[r]));
// l 和 r去重
while (l < r && nums[r] == nums[r - 1]) r--;
while (l < r && nums[l] == nums[l + 1]) l++;
r--;
l++;
}
}
}
}
return res;
}
day08--字符串篇章
lc344 翻转字符串
本题使用双指针 一个卡在开头 一个卡在结尾 ,同时向中间移动 然后交换两个指针指向的数
其中交换数可以使用第三个变量temp 也可以使用位运算不借助任何其他
原理如下:
假设
int a = 13,b = 14
a = a ^ b;
b = a ^ b;
a = a ^ b;
证明: 假设 a是甲,b是乙
a = 甲 ^ 乙
b = 甲 ^ 乙 ^ 乙 = 甲
a = 甲 ^ 乙 = 甲 ^ 乙 ^ 甲 = 乙
注意: a,b两个数必须不同位置,不同地址
本题注意 如果要携程
s[l] = s[l] ^ s[r]; s[r] = s[l] ^ s[r]; s[l] = s[l] ^ s[r];
需要进行类型转换 (char)
s[l] = (char) (s[l] ^ s[r]); s[r] = (char) (s[l] ^ s[r]); s[l] = (char) (s[l] ^ s[r]);
而使用^= 会自动进行类型转换
public void reverseString(char[] s) {
int l = 0, r = s.length - 1;
while(l < r){
s[l] ^= s[r];
s[r] ^= s[l];
s[l] ^= s[r];
l++;
r--;
}
}
解法二: 队列
因为队列是先进后出 入栈之后 再取出自动完成倒序了 但是缺点是消耗内存
public void reverseString(char[] s) {
Stack<Character> stack = new Stack<>();
// 将所有字符压入栈中
for (char c : s) stack.push(c);
// 将字符从栈中弹出,依次放回数组
int i = 0;
while (!stack.isEmpty()) s[i++] = stack.pop();
}
lc541翻转字符串II
给定一个字符串 s 和一个整数 k,从字符串开头算起,�每计数至 2k 个字符,就反转这 2k 字符中的前 k 个字符。�
剩余字符少于 k 个,则将剩余字符全部反转。�
如果剩余字符小于 2k 但大于或等于 k 个,则反转前 k 个字符,其余字符保持原样。�
题目意思是 假设字符串是"12345678" k= 3
其中2k也就是6 翻转前k也就是翻转1-3 剩余78 不够k 就全部翻转
变成"32145687"
因为每次都是2k 所以for循环时候 直接i+=2k
public String reverseStr(String s, int k) {
char[] ch = s.toCharArray();
// 1. 每隔2k翻转前k
for(int i = 0; i < ch.length; i += 2 * k){
// 2. 剩余 >=x并且<2k 那就翻转前k
if(i + k <= ch.length){
reverse(ch, i, i + k - 1);
continue;
}
//3. 剩余的<k 那就把剩余的全部翻转
reverse(ch, i, ch.length - 1);
}
return new String(ch);
}
public void reverse(char[] ch, int i, int j) {
while (i < j){
ch[i] ^= ch[j];
ch[j] ^= ch[i];
ch[i] ^= ch[j];
i++;
j--;
}
}
替换数字
给定一个字符串 s,它包含小写字母和数字字符,请编写一个函数,将字符串中的字母字符保持不变,而将每个数字字符替换为number。
例如,对于输入字符串 "a1b2c3",函数应该将其转换为 "anumberbnumbercnumber"。
第一步 肯定要先把数组扩容到能够容纳转换后的大小
比如原本 "a5b" 的长度为3 那么转换后就是"anumberb" 长度为 8。
然后使用双指针 从后向前替换掉数字 i指针指向新长度的尾巴 j指向旧长度的尾巴
从旧数组 从后向前 开始赋值到新数组 新数组也是后向前便利将s[j]赋值给s[i]
因为从后往前就可以避免元素的移动
本题使用oj模式
// 先把原数组复制到扩展长度后的新数组,然后不再使用原数组、原地对新数组进行操作。
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
String s = sc.next();
int len = s.length();
for (int i = 0; i < s.length(); i++) {
if (s.charAt(i) >= 0 && s.charAt(i) <= '9') {
len += 5;
}
}
char[] ret = new char[len];
for (int i = 0; i < s.length(); i++) {
ret[i] = s.charAt(i);
}
for (int i = s.length() - 1, j = len - 1; i >= 0; i--) {
if ('0' <= ret[i] && ret[i] <= '9') {
ret[j--] = 'r';
ret[j--] = 'e';
ret[j--] = 'b';
ret[j--] = 'm';
ret[j--] = 'u';
ret[j--] = 'n';
} else {
ret[j--] = ret[i];
}
}
System.out.println(ret);
}
}
day9
lc151 翻转字符串的单词
给定一个字符串,逐个翻转字符串中的每个单词。
示例 1:
输入: "the sky is blue"
输出: "blue is sky the"注意: 1. 输入字符串可以在前面或者后面包含多余的空格,但是反转后的字符不能包括。
- 如果两个单词间有多余的空格,将反转后单词间的空格减少到只含一个。
从题目提取的信息: 1. 依照单词为单位进行翻转(字母顺序不能变)
- 结果的前后不能有空格
- 单词之间如果有多个空格 只保留一个
翻转思路: "the sky is blue"
- 先不管字母顺序 整体进行翻转 保证单词的位置一致---变成 "eulb si yks eht"
- 再翻转单词 确保单词顺序 "blue is sky the"
所以整体思路就是
- 移除多余的空格
- 先全部翻转句子
- 翻转单词
class Solution {
public String reverseWords(String s) {
char[] chars = s.toCharArray(); // 先转成字符数组
chars = delSpaces(chars); // 1. 处理空格
reverse(chars, 0, chars.length - 1); // 2.翻转句子
reverseEasyWord(chars); // 3. 翻转单词
return new String(chars);
}
public char[] delSpaces(char[] c){
int s = 0;
for(int f = 0; f < c.length; f++){
if(c[f] != ' ') {
if(s != 0) c[s++] = ' ';
while(f < c.length && c[f] != ' ') c[s++] = c[f++];
}
}
char[] newChar = new char[s];
System.arraycopy(c, 0, newChar, 0, s);
return newChar;
}
public void reverse(char[] c, int l , int r){
if(c.length <= r) return;
while(l < r){
c[l] ^= c[r];
c[r] ^= c[l];
c[l] ^= c[r];
l++;
r--;
}
}
public void reverseEasyWord(char[] c){
int start = 0;
for(int end = 0; end <= c.length; end++){
if(end == c.length || c[end] == ' '){
reverse(c, start, end - 1);
start = end + 1;
}
}
}
}
右旋字符串�
字符串尾部的若干个字符转移到字符串的前面。给定一个字符串 s 和一个正整数 k,请编写一个函数,将字符串中的后面 k 个字符移到字符串的前面,实现字符串的右旋转操作。
对于输入字符串 "abcdefg" 和整数 2,函数应该将其转换为 "fgabcde"。
思路:
把字符串分成两部分 第一段是字符串的长度-n 第二段长度是n 也就是转换成 把第二段放在开头 把第一段放在后面
先不考虑整体顺序 把整体进行翻转 然后再来一次翻转
import java.util.*;
public class Main{
public static void main (String[] args) {
Scanner sc = new Scanner(System.in);
int n = Integer.parseInt(sc.nextLine());
String s = sc.nextLine();
int len = s.length();
char[] c = s.toCharArray();
// 翻转整体
reverString(c, 0, len - 1)
// 原本的第二段变成了第一段 所以开始是0 结束是n-1
reverString(c, 0, n - 1);
// 翻转原本的第一段
reverString(c, n, len - 1);
System.out.println(c);
}
public static void reverString(char[] ch, int l ,int r){
while (l < r){
ch[l] ^= ch[r];
ch[r] ^= ch[l];
ch[l] ^= ch[r];
l++;
r--;
}
}
}
KMP算法基础
理论基础
当出现字符串不匹配时,可以记录一部分之前已经匹配的文本内容,利用这些信息避免从头再去做匹配。
假设 文本串是"aabaabaaf" 目标是"aabaaf" 求文本串是否出现了目标串
字符串1 aabaabaaf
字符串2 aabaaf
kmp算法就是字符串2 在f不匹配的位置 他会跳到b也就是之前匹配过的内容
那么如何找到b呢 就是使用**前缀表 **找到不匹配f的前面是aa 那么就找到aa相等的前缀的后面 重新开始匹配
什么是前缀什么是后缀? aabaaf
前缀是包含首字母 不包含尾巴的所有子串 也就是 a aa aab aaba aabaa
后缀是包含尾巴 不包含开头的所有子串 f af aaf baaf abaaf
最长相等前后缀
a 因为即是开头又是结尾 所以是没有前后缀
aa 前缀a 后缀a 所以1
aab 因为开头a结尾b 所以找不到相等 是0
aaba 前缀是aab 后缀aba 相等的是a 所以长度是1
aabaa 前缀aaba 后缀是abaa 相同是aa 长度为2
aabaaf 前缀aabaa 后缀是abaaf 因为f在前缀中不存在 所以是0
所以aabaaf的前缀表就是[0 1 0 1 2 0] 那么是怎么匹配的呢
文本串 a a b a a b a a f
模式串 a a b a a f
前缀表 0 1 0 1 2 0
遇到f不匹配了 找前面最长相等前后缀 也就是2 也就意味着 有个后缀aa 前面也有个相同的aa
然后跳到前面相等的前缀后面 也就是aa的后面 就是b
在kmp算法中都会提到next数组
是遇到冲突的地方之后next数组会告诉我们回退到哪里
会把前缀表做个右移的操作 或者统一减一的操作
代码实现
在代码实现中分为下面步骤
- 初始化 next数组 各个变量 2. 处理前后缀不相同的情况 3. 相同的情况 4. 更新next
这个2也就意味着需要跳到下标为2的元素上继续匹
- 初始化
j是指向前缀末尾位置 初始化为0
i是指向后缀末尾位置 在for里面1开始
- 前后缀不相同情况
也就s[i] != s[j] 但是要保证j >0 j向前回退 看前一位的前缀表对应下标 j = next[j - 1]
- 前后缀相同的情况
也就是 if(s[i] == s[j]) j++;
- 更新next
next[i] = j
day10--栈and队列
栈: 先进后出 像弹夹 子弹压堂
队列: 先进先出 像管道 双端都有口
Lc232 用栈实现队列
使用栈实现队列的下列操作
push(x) -- 将一个元素放入队列的尾部。
pop() -- 从队列首部移除元素。
peek() -- 返回队列首部的元素。
empty() -- 返回队列是否为空。
public class Lc232_myQueue {
Stack<Integer> sIn, sOut;
public Lc232_myQueue() {
sIn = new Stack<>(); //进栈
sOut = new Stack<>(); //出栈
}
public void push(int x) {
sIn.push(x);
}
public int pop() {
dumpStackIn();
return sOut.pop();
}
public int peek() {
dumpStackIn();
return sOut.peek();
}
public boolean empty() {
return sIn.isEmpty() && sOut.isEmpty();
}
// 如果出栈为空 那么就将In中的元素全部放入Out里面
private void dumpStackIn() {
if(!sOut.isEmpty()) return;
while (!sIn.isEmpty()) sOut.push(sIn.pop());
}
}
Lc225. 用队列实现栈
使用队列实现栈的下列操作:
- push(x) -- 元素 x 入栈
- pop() -- 移除栈顶元素
- top() -- 获取栈顶元素
- empty() -- 返回栈是否为空
一个队列在模拟栈弹出元素的时候只要将队列头部的元素(除了最后一个元素外) 重新添加到队列尾部,此时再去弹出元素就是栈的顺序了。
class Lc225_myStack {
Queue<Integer> q;
public Lc225_myStack() {
q = new ArrayDeque<>();
}
public void push(int x) {
q.add(x);
}
public int pop() {
rePosistion();
return q.poll();
}
public int top() {
rePosistion();
int res = q.poll();
q.add(res);
return res;
}
public boolean empty() {
return q.isEmpty();
}
private void rePosistion() {
int size = q.size();
size--;
//只要 size 仍然大于 0,就继续循环,同时在每次循环中 size 会减 1。
while (size-- > 0) q.add(q.poll());
}
}
Lc20有效的括号
给定一个只包括 '(',')','{','}','[',']' 的字符串 s ,判断字符串是否有效。�
其实总的来说不匹配的情况一共有三种
- 左边( 多余
在便利字符串的时候 遇到了左的({[ 就把对应的右括号放入栈内
如果便利的时候遇到了右边的 就弹出对应栈内的括号
如果字符串遍历完了 但是栈不为空 说明 不匹配 多了
- (} 类型不匹配
遇到相同方向的 但是对比发现类型不一样
- 右边多了
字符串还没遍历完 栈就空了
public boolean isValid(String s) {
// 如果长度是奇数 那一定不满足要求
if(s.length() % 2 != 0) return false;
Deque<Character> deque = new LinkedList<>();
char ch;
for(int i = 0; i < s.length(); i++){
ch = s.charAt(i);
if(ch == '(') deque.push(')');
else if (ch == '{') deque.push('}');
else if(ch == '[') deque.push(']');
// 情况23
else if (deque.isEmpty() || deque.peek() != ch) return false;
else deque.pop();
}
// 情况1 字符串便利完了 但是栈不为空
return deque.isEmpty();
}
Lc1047. 删除字符串中的所有相邻重复项�
本题和上题的匹配括号类似, 本题是匹配相邻元素,最后都是做消除的操作
那么栈的目的,就是存放遍历过的元素,当遍历当前的这个元素的时候,去栈里看一下我们是不是遍历过相同数值的相邻元素。 然后再去做对应的消除操作
class Solution {
public String removeDuplicates(String s) {
ArrayDeque<Character> q = new ArrayDeque<>();
char ch;
for(int i = 0; i < s.length(); i++){
ch = s.charAt(i);
if(q.isEmpty() || q.peek() != ch) q.push(ch);
else q.pop();
}
String res = "";
while(!q.isEmpty()) res = q.pop() + res;
return res;
}
}
day11
Lc150. 逆波兰表达式求值
逆波兰表达式其实就是后缀表达式 是指运算符写在后面。 使用栈来求解
遇到数字就放入栈内 遇到操作符就****取出栈顶两个数字进行计算,并将结果压入栈中
注意:
在本题要注意: 减法和除法 是对前后两个顺序有要求 后弹出的减去 或者除以先弹出的. �因为在栈中,后进先出会导致先压入的元素在减法时应该作为减数,后压入的元素应作为被减数。 所以 减法的写法是 -d.pop() + d.pop() 如果不想这样写 就换成除法一样 两个int
public int evalRPN(String[] tokens) {
Deque<Integer> d = new LinkedList<>();
for(String s : tokens){
if("+".equals(s)) d.push(d.pop() + d.pop());
else if("-".equals(s)) d.push(-d.pop() + d.pop());
else if("*".equals(s)) d.push(d.pop() * d.pop());
else if("/".equals(s)) {
int n1 = d.pop();
int n2 = d.pop();
d.push(n2 / n1);
}else d.push(Integer.valueOf(s));
}
return d.pop();
}
LC239.滑动窗口最大值
使用单调队列 也就是维护队列里面单调递增或者递减
day12-二叉树
基础概念
树:
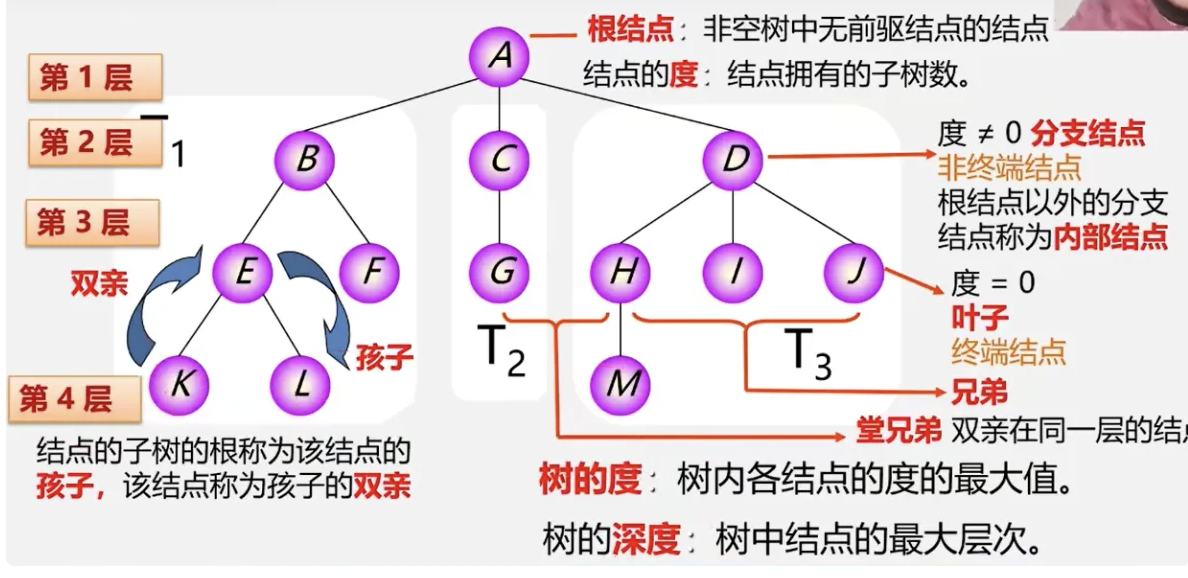
- 树的度:树内各个节点的最大值, 比如节点a 有3个节点,那度就是3
- 叶子节点(终端节点):他的度为0,比如i j
- **孩子、双亲: **比如a节点,他有3个子树t1,t2,t3 那这三个子树的根节点是bcd,那a节点的孩子就是bcd。bcd的双亲就是a
- 兄弟节点: 如果节点有共同的双亲,那他们就是兄弟节点,比如hij的双亲都是d,那hij是兄弟节点
- 树的层: 横着来 有多少层
- 堂兄弟: 他们的双亲位于同一层
- 节点的祖先: 从根到该节点所经过分支上的所有节点,比如a到m需要经过a_d_h。那adh都是m的祖先
- 节点的子孙:以某节点为跟的子树中的任意节点都是该节点的子孙
- **树的深度(高度): 树中节点的最大层次 **
**满二叉树: **
如果一颗二叉树只有度为0的节点和 度为2的节点 并且度为0的节点在同一层上, 就是满二叉树
这棵二叉树为满二叉树,也可以说深度为k,有2^k-1个节点的二叉树。
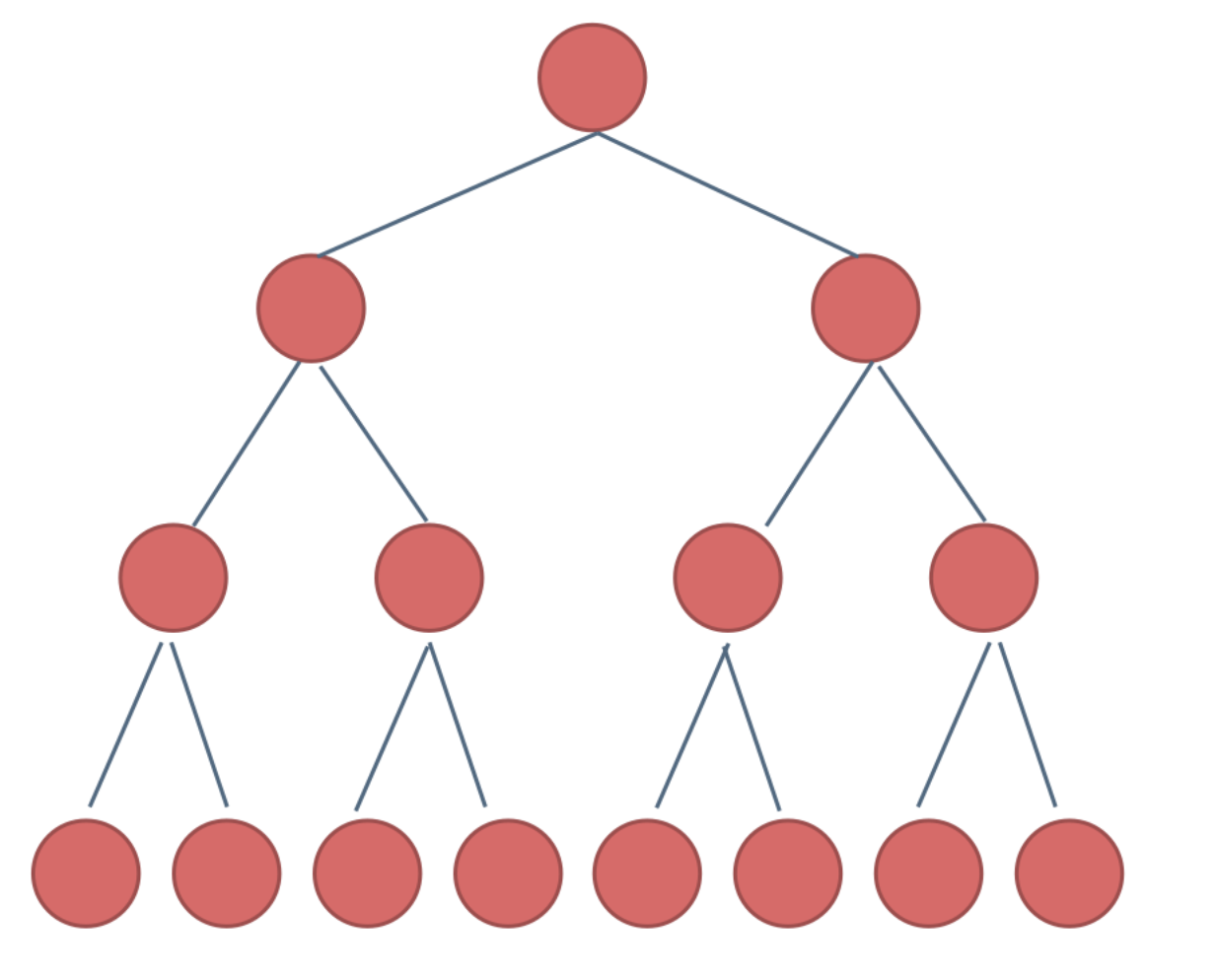
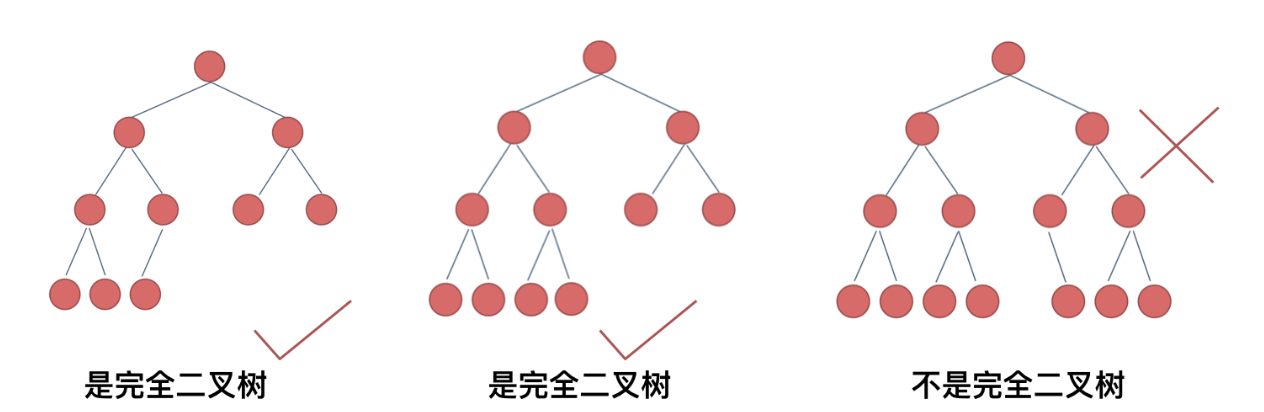
完全二叉树::
除了最底层节点可能没有填满之外,其余的每一层的节点都达到了最大值,并且最下面一层的节点都几种在该层的最左边的若干位置, 如果最底层是h层 那么该层包含1~2^(h-1)个节点
大白话就是 左边节点/全是满的 不能缺 一旦缺少左边节点就不是了
平衡二叉树::(AVL)
一颗空树 或者他的左右两个子树的高度差的绝对值不能超过1 并且左右两个子树都是AVL
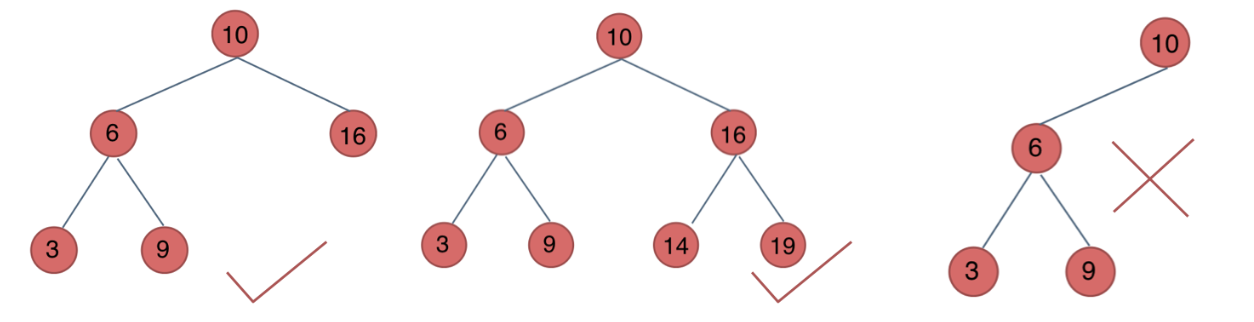
最后一棵 不是平衡二叉树,因为它的左右两个子树的高度差的绝对值超过了1。
二叉树的存储方式
链式存储(指针):通过指针把分布在各个地址的节点串联一起。
顺序存储(数组):
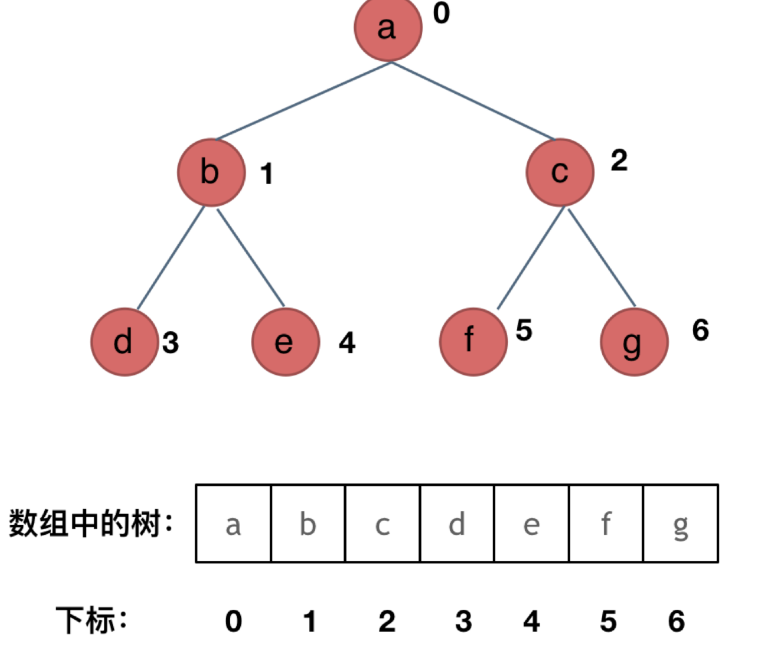
如果父节点的数组下标是 i,那么它的左孩子就是 i * 2 + 1,右孩子就是 i * 2 + 2。 但一般常用链式存储
二叉树的遍历
一. 深度优先遍历(看头在哪 也就是中间节点)
- 先序遍历: 头 -> 左 -> 右
- 中序遍历: 左 -> 头 -> 右
- 后序遍历: 左 -> 右 -> 头
二. 广度优先遍历
也就是层次遍历, 使用队列先进先出的特点 因为先进先出所以才能一层一层的便利
Java中二叉树定义
public class Node{
int v;
Node l;
Node r;
Node(){
}
Node(int v){
this.v = v;
}
Node(int v, Node l, Node r){
this.v = v;
this.l = l;
this.r = r;
}
}
二叉树遍历代码(递归)
节点的定义 如上, 下面代码不再定义节点
// 调用递归方法
public List<Integer> preorderTraversal(Node root) {
List<Integer> res = new ArrayList<>();
prePrint(root, res);
// midPrint(root, res);
// postPrint(root, res);
return res;
}
// lc144---前序便利 跟左右
public void prePrint(Node root, List<Integer> res) {
if(root == null) return;
res.add(root.v);
prePrint(root.l, res);
prePrint(root.r, res);
}
// lc94----中序遍历 左跟右
public void midPrint(Node root, List<Integer> res) {
if(root == null) return;
midPrint(root.l, res);
res.add(root.v);
midPrint(root.r, res);
}
// lc145---- 后续便利 左右跟
public void postPrint(Node root, List<Integer> res) {
if(root == null) return;
postPrint(root.l, res);
postPrint(root.r, res);
res.add(root.v);
}
朋友们,有没有发现一个规律呢?
就是主要看add行为在哪里 add在前面就是根左右--前序 中间就是左跟右--中序 最后就是左右跟-后续
为什么能由一个递归函数来实现呢? 递归序
二叉树便利(迭代法)
使用栈, 压栈, 因为栈是先进后出 注意进出的顺序
使用栈前序便利
思路:
- 创建个Stack栈 并且放入头结点
- while便利 不为空时候 立马pop出头
- 先压入右 再压入左
// lc144---前序便利 跟左右
public List<Integer> prePrint(Node root) {
List<Integer> res = new ArrayList<>();
if(root == null) return res;
Stack<Node> s = new Stack<>();
s.push(root);
while(!s.isEmpty()){
root = s.pop();
res.add(root.v);
if(root.r != null) s.push(root.r);
if(root.l != null) s.push(root.l);
}
return res;
}
后遍历
**在前序便利是跟左右 入栈是先右再左. 那么后序遍历左右跟 改成 入栈 是跟右左 然后再把数组做一个翻转 就变成了左右跟 **
只需要在前序的基础上 入栈顺序改成先左再右 然后再使用库函数做一个翻转
public List<Integer> postPrint(Node root) {
List<Integer> res = new ArrayList<>();
if(root == null) return res;
Stack<Node> s = new Stack<>();
s.push(root);
while(!s.isEmpty()){
root = s.pop();
res.add(root.v);
if(root.l != null) s.push(root.l);
if(root.r != null) s.push(root.r);
}
Collections.reverse(res);
return res;
}
中序遍历
中序遍历是 左跟右 在入栈时候关键在于先一直将左子节点压入栈,直到到达左子树的尽头,然后开始出栈访问节点,最后处理右子节点。
public List<Integer> midPrint(Node root){
List<Integer> res = new ArrayList<>();
if(root == null) return res;
Stack<Node> s = new Stack<>();
Node cur = root;
while (cur != null && !s.isEmpty()){
// 1. 遍历左子节点,将当前节点压入栈,并将 cur 移动到左子节点
if(cur != null){
s.push(cur);
cur = cur.l;
}else {
// 2. 如果当前节点为空(说明已经到达左子树的尽头)
// 从栈中弹出节点,访问该节点并将其值加入结果列表
cur = s.pop();
res.add(cur.v);
// 3. 然后将 cur 移动到右子节点,继续对右子树进行相同操作
cur = cur.r;
}
}
return res;
}
二叉树前中后统一模版
在上面中序遍历中, 提到使用栈无法同时解决访问节点(遍历节点)和处理节点(将元素放进结果集)不一致的情况。 那我们就将访问的节点放入栈中,把要处理的节点也放入栈中但是要做标记。
,就是要处理的节点放入栈之后,紧接着放入一个空指针作为标记。 这种方法也可以叫做标记法。
// 先序遍历
public List<Integer> prePrint(Node root) {
List<Integer> res = new ArrayList<>();
Stack<Node> s = new Stack<>();
if (root != null) s.push(root);
while (!s.isEmpty()){
Node cur = s.peek();
if(cur != null){
s.pop();
if(cur.r != null) s.push(cur.r);
if(cur.l != null) s.push(cur.l);
s.push(cur);
s.push(null);
}else{
s.pop();
cur = s.peek();
s.pop();
res.add(cur.v);
}
}
return res;
}
// 后
public List<Integer> postPrint(Node root){
List<Integer> res = new ArrayList<>();
Stack<Node> s = new Stack<>();
if(root != null) s.push(root);
while (!s.isEmpty()){
Node cur = s.peek();
if(cur != null){
s.pop();
s.push(cur);
s.push(null);
if(cur.l != null) s.push(cur.l);
if(cur.r != null) s.push(cur.r);
}else{
s.pop();
cur = s.peek();
s.pop();
res.add(cur.v);
}
}
return res;
}
/**
* 中序遍历
* @param root
* @return
*/
public List<Integer> midPrint(Node root){
List<Integer> res = new ArrayList<>();
Stack<Node> s = new Stack<>();
if (root != null) s.push(root);
while (!s.isEmpty()){
Node cur = s.peek();
if(cur != null){
s.pop();
if(cur.r != null) s.push(cur.r);
s.push(cur);
s.push(null);
if (cur.l != null) s.push(cur.l);
}else {
s.pop();
cur = s.peek();
s.pop();
res.add(cur.v);
}
}
return res;
}
仔细观察 重点在if(cur != null)上面 else等于空的情况是一样的 所以可以抽象出一个模版框架
public List<Integer> xxxPrint(Node root){
List<Integer> res = new ArrayList<>();
Stack<Node> s = new Stack<>();
if(root != null) s.push(root);
while(!s.isEmpty()){
Node cur = s.peek();
if(cur != null){
s.pop();
// ....
// ....
// ....
// ....
}else{
s.pop();
cur = s.peek();
s.pop();
res.add(cur.v);
}
}
return res;
}
那么代码里面的不等于空的时候怎么写呢?
通过调整节点入栈顺序和null标记的位置,可以实现不同的遍历顺序:
- 前序遍历:右r - 左l - 根 +
null
因为前序便利是跟左右 那么入栈就是 右左跟 再来push一个null
if(cur.r != null) s.push(cue.r);
if(cur.l != null) s.push(cue.l);
s.push(cur);
s.push(null);
- 中序遍历:右 - 根 +
null- 左
中序遍历是左跟右 入栈就是右 跟 null 左
if(cur.r != null) s.push(cue.r);
s.push(cur);
s.push(null);
if(cur.l != null) s.push(cur.l);
- 后序遍历:根 +
null- 右 - 左
后续便利是左右跟 入栈是 跟 null 右 左
s.push(cur);
s.push(null);
if(cur.r != null) s.push(cue.r);
if(cur.r != null) s.push(cue.r);


 浙公网安备 33010602011771号
浙公网安备 33010602011771号