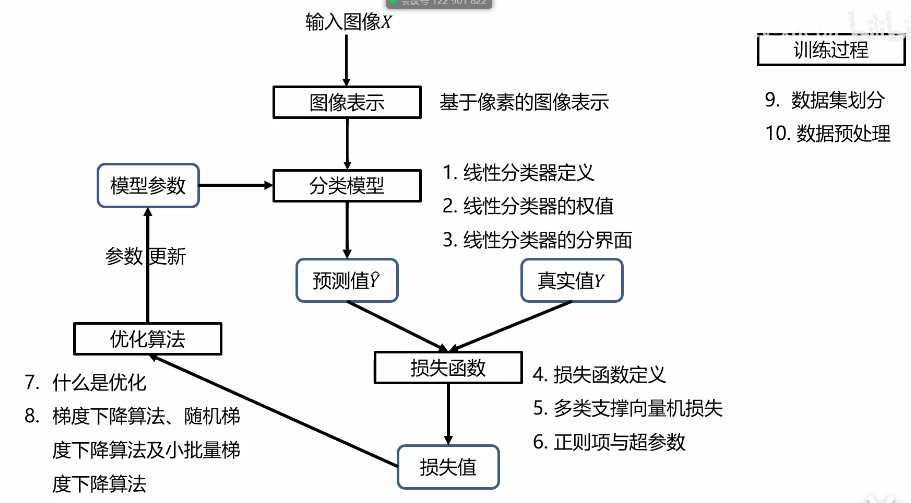
计算机视觉-线性分类器

线性分类器

---

CIFAR10数据集。

 

  

图像类型：

二进制图像（非黑即白，非0即1）、灰度图像（像素值0-255）、彩色图像（RGB，每一个通道都是255个像素值）。

大多数分类算法都要求输入向量。

将图像转换成向量的方法有很多，最直接简单的方法就是将图像矩阵转换成向量（一次排列每一个像素点的RGB就得到了向量）。

 

线性分类器：

为什么从线性分类器开始？

形式简单、易于理解；最重要的是线性分类器可以通过层级结构（神经网络）或者高维映射（支持向量机）可以组合成为功能强大的非线性模型。

线性分类器是神经网络的基础。线性分类器是支持向量机的基础。小样本情况下，支持向量机是绝对的王者；在大样本情况下，神经网络是绝对的王者。

将X向量转换为类别标签。

每一个类别都有自己的参数W和偏置b。这里是假设1000个样本分为10类，这这10类样本就各自有各自的W和b。

决策规则：如果fi（x）>fj（x），i≠j，则决策输入图像x属于第i类。也就是某一个类别x在第i类的打分比第j类的打分高的话，那么就将它归属于第i个类别。

 

损失函数：

损失函数是一个函数，用于度量给定分类器的预测值与真实值的不一致程度，其输出通常是一个非负实值。

损失函数的输出值可以作为反馈信号来对分类器参数进行调整，以降低当前实例对应的损失值，从而提升分类器的分类效果。

 

 

 

  

正则项：

因为不止存在一个权重W能够使得损失函数L=0，因此，在多个权重值之间做出选择时就需要用到正则项。

 

 超参数：在开始学习过程之前设置的参数；超参数一般都会对模型性能有着重要的影响。

使用L2正则项：R(W)=求和（Wi^2），选择正则损失最小的那个权重W值。

L2正则损失对大数值权值进行惩罚，喜欢分散权值，鼓励分类器将所有维度的特征都用起来，而不是强烈的依赖其中少数几维特征。

L2正则过程中会选择尽量多的考虑到所有的维度特征，而不是简单依赖于其中某一个或几个特征就得出结果，避免了某个重要维度出现损伤的情况下导致整体出错。也就是避免了对其中某些少数维度的强依赖性。同时防止模型过拟合。

 

优化函数：

参数优化是机器学习的核心步骤之一，它利用损失函数的输出值作为反馈信号来调整分类器参数，以提升分类器对训练样本的预测性能。

优化的目标：找到使损失函数L达到最优的那组参数W。直接方法就是L对W求偏导等于0，这里表示找到一个W使得L函数得到极值点。但是通常情况下，L的形式非常复杂，很难通过简单的等式求解出来W。

梯度下降算法：往负梯度方向走，步长由学习率决定。基本思想是逐步迭代得到最终结果，我们无法获得全局位置，但是我们知道当前位置，利用当前位置我们可以知道向负梯度方向走，也就是使得损失变小的方向，每一步跨多远是由学习率决定的。

梯度计算过程中有两种方法：数值法和解析法。

数值法：使用偏导数求极限的思想得到近似解。

解析法：直接通过求导的方式得到结果。

求梯度的过程中一般使用解析法求梯度，而数值法主要用于解析法结果的正确性校验（梯度检查）。因为解析法虽然精确，速度快，但是容易出错。因此使用数值法的结果来校验，如果两者结果相近，则说明数值法是准确的。

缺点：当N很大时，权值的梯度计算量很大，更新的就会很慢，效率低下。

随机梯度下降算法：

每次随机选择一个样本计算损失并更新梯度。

缺点：单个样本的训练可能会带来很多噪声，不是每一次迭代都想着整体最优化的方向。

小批量梯度下降算法：

每次随机选择m小批量个样本计算损失并更新梯度。

这里的m一般取2的倍数。

batch_size：每次迭代所使用的的样本量。

epoch：表示一共要迭代多少次。

数据集划分：

训练集用于给定的超参数时分类器参数的学习；验证集用于选择超参数；测试集评估泛化能力。

如果数据样本很少，那么可能验证集包含的样本就太少。这个时候就需要使用到K折交叉验证的方法来进行训练。/带打乱数据的K折交叉验证，过程基本与K折交叉验证相同，不同的是每次划分训练集和验证集时都需要打乱数据集。

数据预处理：

1.去均值。2. 归一化。1. 去相关（数据的协方差矩阵是对角矩阵）。2. 白化数据（协方差矩阵是单位矩阵）。

后1,2常用作传统的支持向量机，机器学习中来处理数据。前1,2是在神经网络深度学习中常使用的方法。