2.1 变量的数据类型

例 2-1

跑步。小 A 的跑步速度为 5m/s，八位勇跑步的速度为 8m/s，八位勇在小 A 后面 100m，他们同时起跑。

请问：需要多长时间八位勇可以追上小 A ？输出一个数字表示答案。

建模分析：

八位勇落后 100m，但是速度快，只要八位勇比小 A 快的速度 (8-5)m/s 跑完落后的 100m ，即追上小 A，所以问题转化成 3m/s 的速度，多久可以跑完 100m。

#include<iostream>
using namespace std;

int main()
{
    cout<<100.0/(8-5)<<endl;
    return 0;
}

书本上为了介绍 int 和 double 类型，特意定义了多个变量。

这里介绍一下常见的数据类型，

表 2-1

数据类型	占用空间	取值范围
char	1 字节，8 位	-128 ~ 127
int	4 字节，32 位	-231 ~ 231-1,绝对值约 2.1*109
unsigned int	4 字节，32 位	0 ~ 232-1,绝对值约 4.2*109
long long	8 字节，64 位	-263 ~ 263-1,绝对值约 9.2*1018
unsigned long long	8 字节，64 位	0 ~ 264-1,绝对值约 1.8*1019
float	4 字节，32 位	-2128 ~ 2128，绝对值约3.40*1038，6位有效数字
double	8 字节，64 位	-21024 ~ 21024，绝对值约1.79*10308，15位有效数字

float 和 double 能够用和 int，long long 相同的字节存放更大的数值，是因为存放逻辑不一样，有效数字的位数比较少。

例 2-2

英文字母。英文有26个字母，其中 A 是第一个字母。

现在请编程求出：

1. M 是字母表的第几个字母？
2. 第 18 个字母是什么？

输出两个数字，使用换行符隔开。

建模分析：

char字符本质上是 -128 ~ 127 的数字，大写字母 A 的数字编码是 65。那么题目要求 M 是第几个数字，用 'M'-'A'+1 即可得到是第几个数字。
然后 'A'+18-1 即可得到 18 个字母是什么。本质上还是整形的数字运算。

#include<iostream>
using namespace std;

int main()
{
    cout<< 'M'-'A'+1 <<endl;
    
    char n='A'+18-1;
    cout<< n <<endl;
    return 0;
}

输出字符还是数字，按变量类型来决定。

表 2-2

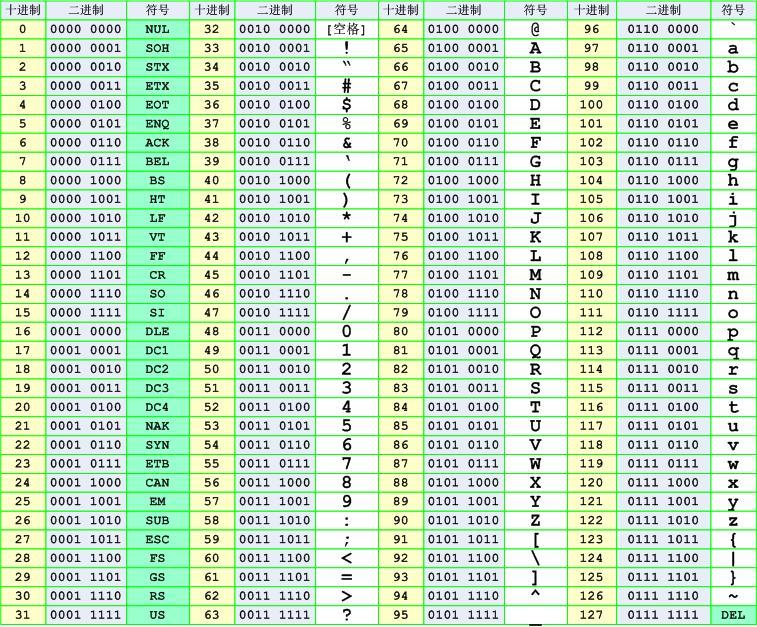
0-31 为不可见字符

char 类型本质上就是0~127的整数。

例 2-3

玩橡皮泥。小 A 有两块球形橡皮泥，一个半径是 4，另一个半径是 10.他想把这两块橡皮泥揉在一起，然后塑造成一个正方体。

请问：这个正方形的边长是多少？如果结果不是整数，则舍去小数点之后的数字。取 π=3.141593.

建模分析：

球形的体积公式是 $ V=\frac{4}{3}πr^3 $,所以总体积是 $ V=\frac{4}{3}π4^3 + \frac{4}{3}π10^3 = \frac{4}{3}π(4^3+10^3) $

正方形的体积公式是 边长的立方，即求到总体积后，做开立方即可得到边长。

$\sqrt[3]{\frac{4}{3}π(4^3+10^3)} $

本质上是数学计算。

#include<iostream>
#include<cmath>
using namespace std;

#define PI 3.141593
int main()
{
    int r1=4,r2=10;
    double v,l;
    v=4.0/3*PI*(pow(r1,3)+pow(r2,3));
    l=pow(v,1.0/3);
    cout<<(int)l<<endl;
    return 0;
}

例 2-4

销量预测。根据咕咕网校的预测，当课程定价为 110 元时，会有 10 人报名。如果课程价格降低 1 元，就会多 1 名报名者，反之亦然。如果希望总共能收到 3500 元学费，那么应该定价多少呢？

已知本题有两个答案符合要求，取较小的那一个。如果这个答案不是整数，则需要四舍五入精确到整数。

建模分析：

解法一：

假设课程降低 x 元，则定价就是 (110-x) 元，报名人数就是 (10+x) 个，可以列出方程式 (110-x)*(10+x)=3500。 经过简化可以得到方程式： x²-100x+2400=0,根据二次元方程式求根公式：

$ x_1,_2=\frac{-b \pm \sqrt{b^2-4ac}}{2a} $

最后取较大那个根即可，这样定价就是较小的那个。

#include<iostream>
#include<cmath>
using namespace std;

int main()
{
    double a=1,b=-100,c=2400;
    double delta,ans;
    delta=pow(b,2)-4*a*c;
    ans=(-b+sqrt(delta))/(2*a);
    cout<<110-int(ans+0.5)<<endl;
    return 0;
}

解法二：

因为价格范围只在 0~110 之间，所以可以通过循环寻找符合条件的数值。

#include<iostream>
using namespace std;

int price=110;
int count=10;
int main()
{
	for(int i=110;i>0;i--)
	{
		if((110-i)*(10+i)>=3500)
		{
			cout<<110-i<<endl;
			break;
		}
	}
	
    return 0;
}