排序1
排序相关名词
1. 排序算法的稳定性(Stability)
◼ 概念 : 如果相等的2个元素,在排序前后的相对位置保持不变,那么这是稳定的排序算法
- 排序前:5, 1, 3𝑎, 4, 7, 3𝑏
- 稳定的排序: 1, 3𝑎, 3𝑏, 4, 5, 7
- 不稳定的排序:1, 3𝑏, 3𝑎, 4, 5, 7
◼ 对自定义对象进行排序时,稳定性会影响最终的排序效果 (比如学生按成绩排序)
◼ 冒泡排序属于稳定的排序算法
- 稍有不慎,稳定的排序算法也能被写成不稳定的排序算法,比如下面的冒泡排序代码是不稳定的
for (int end = array.length - 1; end > 0; end--) {
for (int begin = 1; begin <= end; begin++) {
// <= 会导致相等也会交换
if (cmp(begin, begin - 1) <= 0) {
swap(begin, begin - 1);
}
}
}
2. 原地算法(In-place Algorithm)
概念 :
-
不依赖额外的资源或者依赖少数的额外资源,仅依靠输出来覆盖输入
-
空间复杂度为 𝑂(1) 的都可以认为是原地算法
◼ 非原地算法,称为 Not-in-place 或者 Out-of-place
3. 常见的递推式与复杂度
| 递推式 | 复杂度 |
|---|---|
| T(n) = T (n/2) + O(1) | O(\(logn\)) |
| T(n) = T(n - 1) + O(1) | O(n) |
| T(n) = T(n / 2) + O(n) | O(n) |
| T(n) = 2 * T(n / 2) + O(1) | O(n) |
| T(n) = 2 * T(n / 2) + O(n) | O(\(nlogn\)) |
| T(n) = T(n - 1) + O(n) | O(n2) |
| T(n) = 2 * T(n - 1) + O(1) | O(2n) |
| T(n) = 2 * T(n - 1) + O(n) | O(2n) |
排序算法
10种排序算法
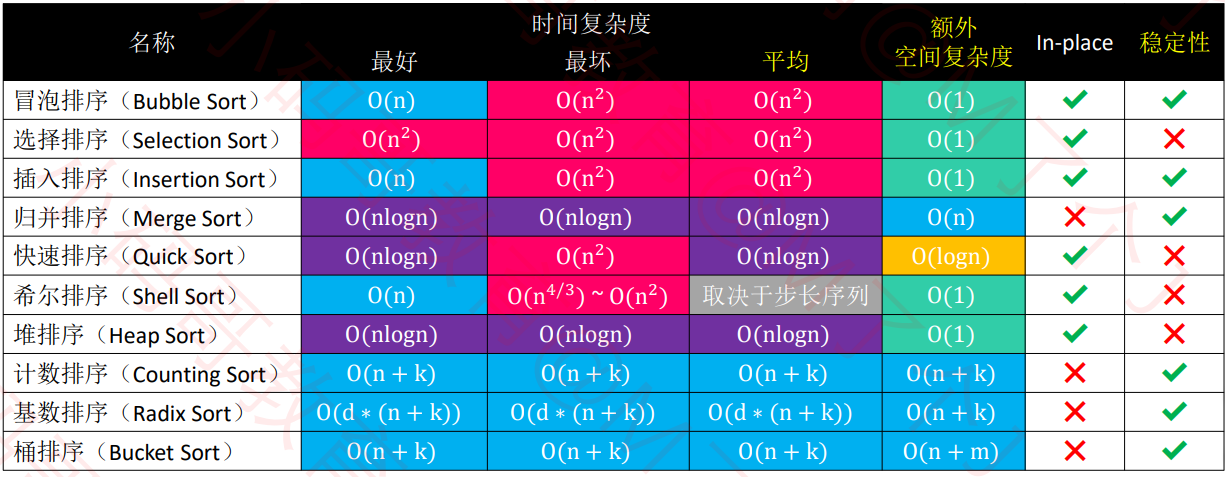
-
以上表格是基于数组进行排序的一般性结论
-
冒泡、选择、插入、归并、快速、希尔、堆排序,属于比较排序(Comparison Sorting)
1. 冒泡排序(Bubble Sort)
◼ 冒泡排序也叫做起泡排序
◼ 执行流程(统一以升序为例子)
- 从头开始比较每一对相邻元素,如果第1个比第2个大,就交换它们的位置
- 执行完一轮后,最末尾那个元素就是最大的元素
- 忽略 ① 中曾经找到的最大元素,重复执行步骤 ①,直到全部元素有序
◼ 时间复杂度最好是O(n) ----- 当数组完全有序时
◼ 时间复杂度最坏是O(n2) ----- 当数组为倒序时(每次都需要交换)
◼ 空间复杂度O(1)
代码实现:
static void bubbleSort1(Integer[] array) {
for (int end = array.length - 1; end > 0; end--) {
for (int begin = 1; begin <= end; begin++) {
if (array[begin] < array[begin - 1]) {
int tmp = array[begin];
array[begin] = array[begin - 1];
array[begin - 1] = tmp;
}
}
}
}
◼ 冒泡排序优化
优化方法1 :
-
如果序列已经完全有序,可以提前终止冒泡排序
-
当某一次遍历不存在交换时 说明数组已经有序 直接退出
-
增加一个\(bool\)值,用于判断一次循环后是否有数据交换,如果没有,则退出排序
-
如果数据不是完全有序,此优化会因多了额外的指令而导致计算时间更长(多了判断)
代码实现:
static void bubbleSort2(Integer[] array) {
for (int end = array.length - 1; end > 0; end--) {
boolean sorted = true; //标记是否进行过交换
for (int begin = 1; begin <= end; begin++) {
if (array[begin] < array[begin - 1]) {
int tmp = array[begin];
array[begin] = array[begin - 1];
array[begin - 1] = tmp;
sorted = false; // 此轮循环进行过交换
}
}
// 没有进行过交换 退出
if (sorted) break;
}
}
优化方法2 :
- 如果序列尾部已经局部有序,可以记录最后1次交换的位置,减少比较次数
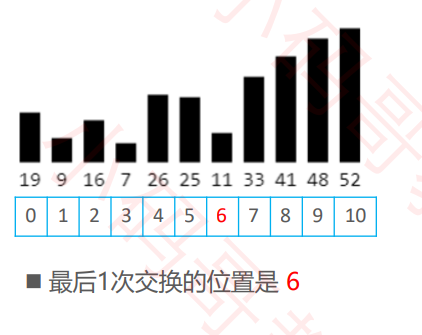
- 记录上一次循环最后一次交换的位置,将其作为下一次循环的截止位置
代码实现:
static void bubbleSort3(Integer[] array) {
for (int end = array.length - 1; end > 0; end--) {
// sortedIndex的初始值在数组完全有序的时候有用
int sortedIndex = 1;
for (int begin = 1; begin <= end; begin++) {
if (array[begin] < array[begin - 1]) {
int tmp = array[begin];
array[begin] = array[begin - 1];
array[begin - 1] = tmp;
sortedIndex = begin;
}
}
// 如果数组在初始就完全有序 end会等于1 直接退出
end = sortedIndex;
}
}
2. 选择排序(Selection Sort)
◼ 执行流程
-
从序列中找出最大的那个元素,然后与最末尾的元素交换位置
-
执行完一轮后,最末尾的那个元素就是最大的元素
-
忽略 ① 中曾经找到的最大元素,重复执行步骤 ①
代码实现:
static void selectionSort(Integer[] array) {
for (int end = array.length - 1; end > 0; end--) {
int maxIndex = 0;
// 找到最大元素的索引
for (int begin = 1; begin <= end; begin++) {
if (array[maxIndex] <= array[begin]) {
maxIndex = begin;
}
}
int tmp = array[maxIndex];
array[maxIndex] = array[end];
array[end] = tmp;
}
}
- 选择排序的交换次数要远远少于冒泡排序,平均性能优于冒泡排序。
- 最好,最坏,平均时间复杂度:O(n2),空间复杂度:O(1)。
- 属于不稳定排序。
3. 堆排序(Heap Sort)
◼ 堆排序可以认为是对选择排序的一种优化 (利用二叉堆找到数组中的最大元素)
- 最好,最坏,平均时间复杂度:$ O(nlogn)$。
- 空间复杂度\(O(1)\),属于不稳定排序。
◼ 执行流程
- 对序列进行原地建堆
(heapify)构成一个大顶堆

- 重复执行以下操作,直到堆的元素数量为 1
-
交换堆顶元素与堆尾元素
-
堆的元素数量减 1
-
对 0 位置进行 1 次
siftDown操作

代码实现:
public class HeapSort<T extends Comparable<T>> extends Sort<T> {
//二叉堆的大小
private int heapSize;
@Override
protected void sort() {
// 原地建堆
heapSize = array.length;
// 自下而上的下滤操作 O(n)
for (int i = (heapSize >> 1) - 1; i >= 0; i--) {
siftDown(i);
}
while (heapSize > 1) {
// 交换堆顶元素和尾部元素
swap(0, --heapSize);
// 对0位置进行siftDown(恢复堆的性质)
siftDown(0);
}
}
private void siftDown(int index) {
T element = array[index];
int half = heapSize >> 1;
while (index < half) { // index必须是非叶子节点
// 默认是左边跟父节点比
int childIndex = (index << 1) + 1;
T child = array[childIndex];
int rightIndex = childIndex + 1;
// 右子节点比左子节点大
if (rightIndex < heapSize && cmp(array[rightIndex], child) > 0) {
child = array[childIndex = rightIndex];
}
// 大于等于子节点
if (cmp(element, child) >= 0) break;
array[index] = child;
index = childIndex;
}
array[index] = element;
}
}
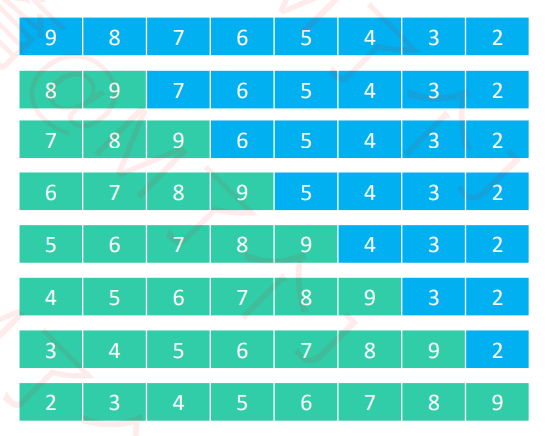
4. 插入排序(Insertion Sort)
◼ 插入排序非常类似于扑克牌的排序

◼ 执行流程
① 在执行过程中,插入排序会将序列分为2部分
✓ 头部是已经排好序的,尾部是待排序的
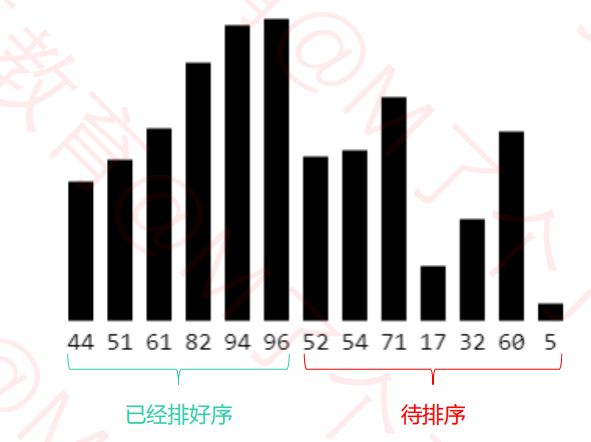
② 从头开始扫描每一个元素
✓ 每当扫描到一个元素,就将它插入到头部合适的位置,使得头部数据依然保持有序
✓ 就是与前面的元素挨个比较 符合条件就交换 直到遇到不符合条件的为止
代码实现:
protected void sort() {
for (int begin = 1; begin < array.length; begin++) {
int cur = begin;
while (cur > 0 && cmp(cur, cur - 1) < 0) {
swap(cur, cur - 1);
cur--;
}
//两种写法
// for (int cur = begin; cur > 0; cur--) {
// if (cmp(cur, cur - 1) >= 0) break;
// swap(cur, cur - 1);
// }
}
}
-
最坏、平均时间复杂度:O(n 2 )
-
最好时间复杂度:O(n)
-
空间复杂度:O(1)
-
属于稳定排序
逆序对(Inversion)
◼ 什么是逆序对?
- 数组 <2,3,8,6,1> 的逆序对为:
<2,1> < 3,1> <8,1> <8,6> <6,1>,共5个逆序对
◼ 插入排序的时间复杂度与逆序对的数量成正比关系
- 逆序对的数量越多,插入排序的时间复杂度越高(交换的次数越多)
◼ 当逆序对的数量极少时,插入排序的效率特别高
- 甚至速度比 \(O(nlogn)\) 级别的快速排序还要快
◼ 数据量不是特别大的时候,插入排序的效率也是非常好的
二分搜索(Binary Search)
- 概念
-
如何确定一个元素在数组中的位置?
-
如果是无序数组,从第0个位置开始遍历搜索,平均时间复杂度:O(n)

-
如果是有序数组,可以使用二分搜索,最坏时间复杂度:O(\(logn\))

-
二分查找操作的数据集是一个有序的数据集
-
二分查找能应用于任何类型的数据,只要能将这些数据按照某种规则进行排序
-
当待搜索的集合是相对静态的数据集时,使用二分查找是最好的选择
-
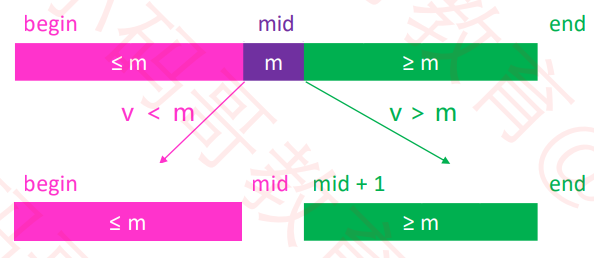
二分搜索 – 思路
-
假设在 [begin, end) 范围内搜索某个元素 V,mid == (begin + end) / 2
-
如果 V < mid,去 [begin, mid) 范围内二分搜索
-
如果 V > mid,去 [mid + 1, end) 范围内二分搜索
-
如果 V == mid,直接返回 mid
-
-
二分搜索 – 实例
- 搜索 10
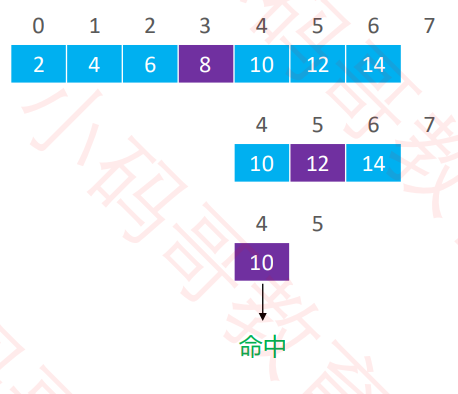
- 搜索 3

- 二分搜索 – 实现
/**
* 查找v在有序数组array中的位置
*/
public static int indexOf(int[] array, int v) {
if (array == null || array.length == 0) return -1;
int begin = 0;
int end = array.length;
while (begin < end) {
int mid = (begin + end) >> 1;
if (v < array[mid]) {
end = mid;
} else if (v > array[mid]) {
begin = mid + 1;
} else {
return mid;
}
}
return -1;
}
- 如果存在多个重复的值,返回的值不确定。
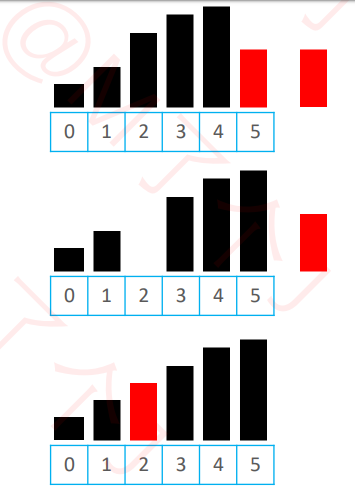
插入排序优化
-
思路是将【交换】转为【挪动】 减少交换次数
① 先将待插入的元素备份
② 头部有序数据中比待插入元素大的,都朝尾部方向挪动1个位置
③ 将待插入元素放到最终的合适位置
代码实现:
// 泛型T protected void sort() { for (int begin = 1; begin < array.length; begin++) { T v = array[begin]; int cur = begin; while (cur > 0 && cmp(v, array[cur - 1]) < 0) { array[cur] = array[cur - 1] ; cur--; } array[cur] = v; } } -
第二种优化(二分搜索优化)(减少比较次数, 由O(n) -> O(\(logn\)))
◼ 在元素 v 的插入过程中,可以先二分搜索出合适的插入位置,然后再将元素 v 插入
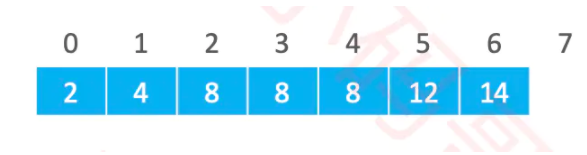
◼ 要求二分搜索返回的插入位置:第1个大于 v 的元素位置
-
如果 v 是 5,返回 2
-
如果 v 是 1,返回 0
-
如果 v 是 15,返回 7
-
如果 v 是 8,返回 5
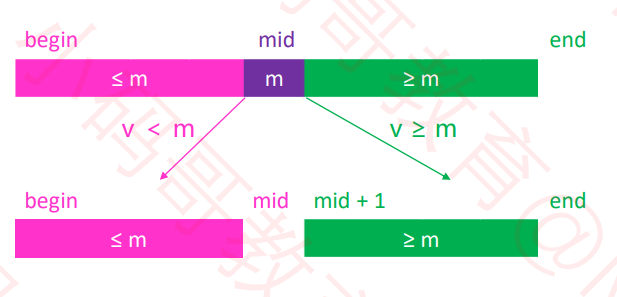
◼ 二分搜索优化 – 思路(找到元素 V 的插入位置)
-
假设在 [begin, end) 范围内搜索某个元素 v,mid == (begin + end) / 2
-
如果 v < m,去 [begin, mid) 范围内二分搜索
-
如果 v ≥ m,去 [mid + 1, end) 范围内二分搜索
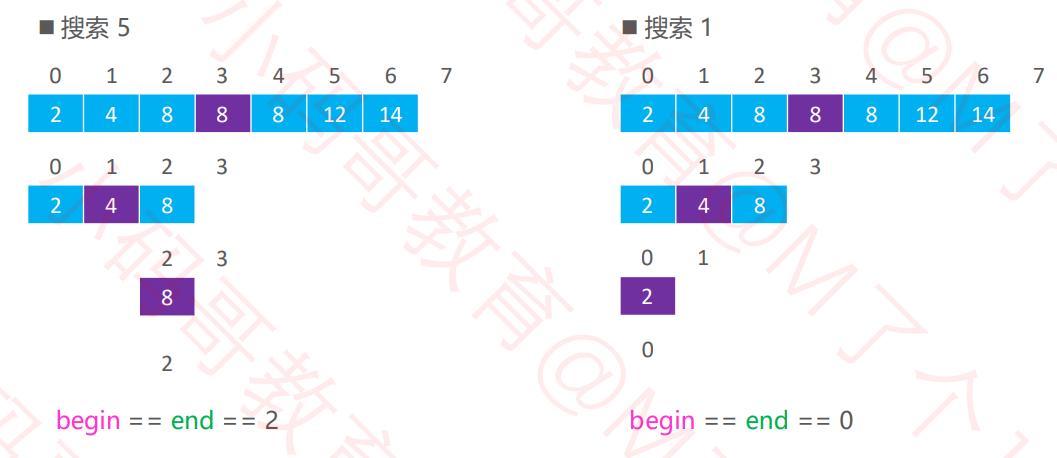
◼ 二分搜索优化 – 实例
当 **begin == end**,即退出。
代码实现:
@Override
protected void sort() {
for (int begin = 1; begin < array.length; begin++) {
insert(begin, search(begin));
}
}
/**
* 将source位置的元素插入到dest位置
*/
private void insert(int source, int dest) {
T v = array[source];
for (int i = source; i > dest; i--) {
array[i] = array[i - 1];
}
array[dest] = v;
}
/**
* 利用二分搜索找到 index 位置元素的待插入位置
* 已经排好序数组的区间范围是 [0, index)
*/
private int search(int index) {
int begin = 0;
int end = index;
while (begin < end) {
int mid = (begin + end) >> 1;
if (cmp(array[index], array[mid]) < 0) {
end = mid;
} else {
begin = mid + 1;
}
}
return begin;
}
- 需要注意的是,使用了二分搜索后,只是减少了比较次数,但插入顺序的平均时间复杂度依旧是O(n2)。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号