快速幂算法

快速幂算法

1. 问题 -- 求2¹⁰⁰的后三位数

​ 思路1 : 直接for循环求解 求出2的100次方再%1000即为后三位数 时间复杂度O(n)

// base 底数  index 指数
long long Pow(long long base, long long index) {
	int res = 1;
	for (int i = 0; i < index; i++) {
		res = res * base;
	}
	return res;
} 
int main()
{			
	cout << Pow(2, 100) % 1000;
	return 0;
} 

​ 结果为0

​ 原因: 由于指数爆炸2的100次方会是一个非常大的数 我们所学的编程语言中没有数据类型能承受如此之大的数 所以产生了溢出

​ 解决办法 利用模运算法则

2. “取模”运算的运算法则

• (a + b) % p = (a % p + b % p) % p （1）

• (a - b) % p = (a % p - b % p ) % p （2）

• (a * b) % p = (a % p * b % p) % p （3)

• (a^b) % p = ((a % p)^b) % p （4）

  我们只需要关注第3条法则 (a * b) % p = (a % p * b % p) % p

推导过程：

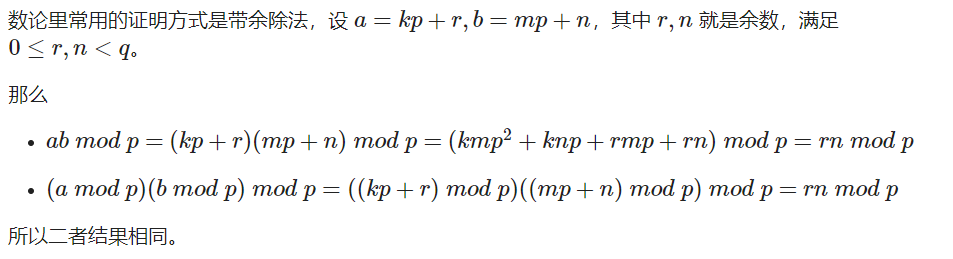
根据上面的推导过程 可以推导出(a * b * c) % p = (a % p * b % p * c % p) % p

所以 (a * b * c * d * ......) = (a % p * b % p * c % p * d % p * ......) % p

所以，借助这个法则，只需要在循环乘积的每一步都提前进行“取模”运算

// base 底数  index 指数
int Pow(int base, int index) {
	int res = 1;
	for (int i = 0; i < index; i++) {
        // 1 * 2 % 1000 * 2 % 1000 * ......
		res = res * base;
		res = res % 1000;
	}
	return res % 1000;
} 
int main()
{			
	cout << Pow(2, 100);
	return 0;
} 

结果 : 376 时间复杂度依旧为O(n) 所以当指数很大时运算需要很长时间 所以需要用到快速幂

3.快速幂

快速幂算法的核心思想是二分法: 每次都将指数/2 底数求平方平方

3¹⁰ = 3 * 3 * 3 * 3 * 3 * 3 * 3 * 3 * 3 * 3 需要10次运算

将其对半分解

3¹⁰ = 3^10=(3 * 3) * (3 * 3) * (3 * 3) * (3 * 3) * (3 * 3) = (3²)⁵ = 9⁵ 此时需要 5次运算

但此时指数为奇数 无法整除2 所以将其分解为

9⁵ = 9⁴ * 9¹

对9⁴继续进行分解

9⁵ = (9 * 9) * (9 * 9) * 9 = (9²)² * 9 = (81)² * 9

对81²进行分解

9⁵ = (81 * 81)¹ * 9 = 6561¹ * 9

此时指数又为奇数 但无法对指数进行压缩操作

将上述流程转化为代码:

long long Pow(long long base, long long index) {
	long long res = 1;
	while (index) {
		if (index % 2 != 0) {  // 指数为奇数  
			// 拆成A^1 和 A^(n - 1) 
			res *= base;
			// 指数减一  由于编程语言中默认向下取整 所以index--可以不写
			//index--; 
		}
		// 到这说明指数为偶数  底数平方 
		base *= base;
		// 指数减半 
		index /= 2;	
	} 	
	return res;
}  

​ 转化为上题代码

long long Pow(long long base, long long index) {
	long long res = 1;
	while (index) {
		if (index % 2 != 0) {
			res = res * base % 1000;
		}
		base = (base * base) % 1000;
		index /= 2;	
	} 	
	return res % 1000;
} 

4.位运算优化

判断一个数是奇数还是偶数可用位运算 如果一个数 a&1 == 0 则这个数为偶数 == 1 为奇数

一个整数右移一位等于该数除以2
a>>1 == a / 2

long long Pow(long long base, long long index) {
	long long res = 1;
	while (index) {
		if (index&1) {
			res = res * base % 1000;
			index--; 
		}
		base = (base * base) % 1000;
		index >>= 1;	
	} 	
	return res % 1000;
}