代码随想录算法训练营day27 | 455. 分发饼干、376. 摆动序列、53. 最大子序和

455. 分发饼干

点击查看代码

class Solution {
public:
    int findContentChildren(vector<int>& g, vector<int>& s) {
        sort(g.begin(), g.end());
        sort(s.begin(), s.end());
        int result = 0;
        /已经分发的饼干不能再分开，故startIndex指向首个还未分发的饼干
        int startIndex = 0;
        for(int i = 0; i < g.size(); ++i) {
            bool iscontent = 0;
            for(int j = startIndex; j < s.size(); ++j) {
                if(s[j] >= g[i]) {
                    ++result;
                    startIndex = j + 1;
                    iscontent = 1;
                    break;
                }
            }
            //剪枝操作，若有一个胃口值是所有饼干都无法满足的，则后续胃口值也必然无法满足
            //因为已经对胃口值排序，所以后续胃口值只会更大
            if(iscontent == 0) break;
        }
        return result;
    }
};

376. 摆动序列

点击查看代码

class Solution {
public:
    int wiggleMaxLength(vector<int>& nums) {
        int result = 1;
        int pre = nums[0];
        //当target == 1时，说明此时要找的是比pre大的
        //当target == 0时，说明此时要找的是比pre小的
        bool target;
        if(nums.size() == 1) return 1;
        int startIndex = 1;
        while(startIndex < nums.size()) {
            if(nums[startIndex] != nums[0]) {
                if(nums[startIndex] - nums[0] > 0) target = 1;
                else target = 0;
                break;
            }
            else ++startIndex;
        }
    
        for(int i = startIndex; i < nums.size(); ++i) {
            if(nums[i] - pre > 0 && target == 1) {
                ++result;
                target = 0;   
            }
            else if(nums[i] - pre < 0 && target == 0) {
                ++result;
                target = 1;
            }
            pre = nums[i];
        }
        return result;
    }   
};

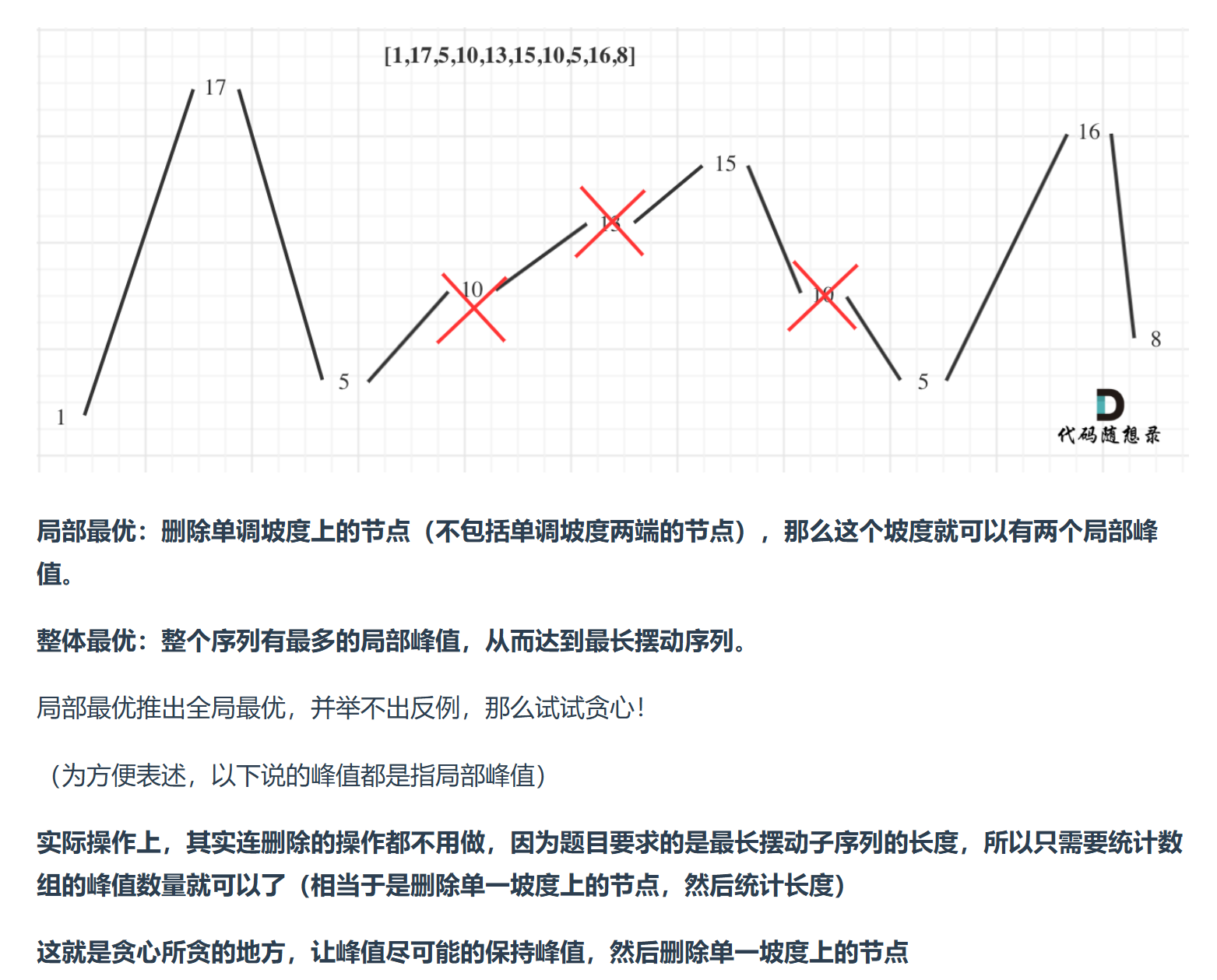
本题将序列画出后可以更直观地看出删除那些值，出现连续递增和连续递减序列均保留首尾元素，体现在pre的更新上

53. 最大子序和

点击查看代码

class Solution {
public:
    int maxSubArray(vector<int>& nums) {
        int result = INT_MIN;
        int count = 0;
        for(int i = 0; i < nums.size(); ++i) {
            count += nums[i];
            //及时更新最大子数组和
            result = max(result, count);
            //核心代码：若子数组和已经变为负数，则必然会拖累后续子数组和
            //故果断抛弃，从i + 1开始重新计算子数组和
            if(count <= 0) {
                count = 0;
            }
        }
        return result;
    }
};

精辟理解：

暴力解法的问题在于，固定子数组起始位置后开始叠加，当叠加值已经为负数时，仍然继续往后叠加，根据常识，最大子数组和必然不可能包含前面这段叠加值为负数的区间，因为这段区间会使整体的叠加值更小，去掉这段叠加值为负数的区间，整体叠加值更大，故贪心算法中，在遇到叠加值为负数的区间后，果断抛弃这段区间，叠加值count清空为0，而从下一个元素nums[i + 1]处重新开始叠加，重新开始找最大子数组。