KMP 算法 （自身理解）

　　给定一个字符串 s , 模式串 p , 寻找 s 子串 与 p 完全匹配

暴力算法：

 

 

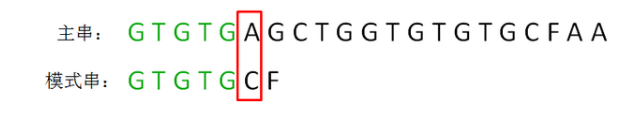
 当遇到不匹配时，当前S不匹配的元素A和P最开始的元素G重新开始匹配

KMP 算法：

前缀是指 不包括字符串最后一位的任意字符串
后缀是指 不包括字符串最开始一位的任意字符串

最大公共前后缀指 前缀和后缀的并集中长度最大的子串

 

 

 当遇到不匹配时，将 最长可匹配后缀和最长可匹配前缀（也是最大公共前后缀）对齐，我们拿最长可匹配前缀下一个元素T和最长可匹配后缀下一个元素A去匹配则可，相等于跳过前3个元素

 对于p中的每个元素，用一个数组记录每个元素的最长可匹配前缀子串的长度。当遇到当前P中元素与S中元素不匹配时，可以快速进行对齐。该长度值存放到next数组中。

 为什么叫做next 数组呢，因为数组下标是从0开始，当找到当前最长可匹配前缀子串的长度时，长度值等于下一个需要匹配的元素下标。

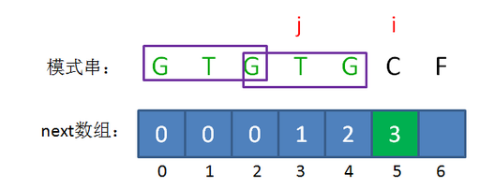
 如在上图中，当前最长可匹配长度是3 ，下一个需要比较的P中元素的下标值也是3，也就是模式串中的T

 next[j] = P.substring(0,j) 中最长可匹配前缀子串的长度值。 

 

 动态规划生成next 数组

状态方程 假设 上一个元素计算得到的最长可匹配的前缀长度为 j , P当前元素下标为 i , 则可以得到

1）如果 P[i-1] == P[j] , next[i] = next[i-1] + 1 。 

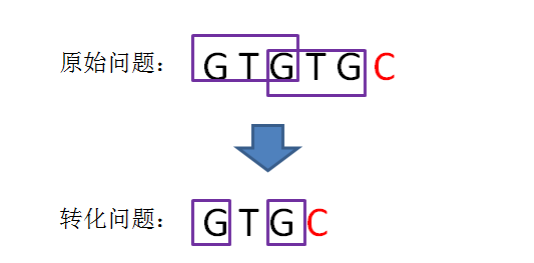
如 next[4] = 2 , 即 说明 P[0][1] 和 P[2][3] 是匹配的（最长可匹配前缀 和 后缀都是 2 ）， 如果 P[2] == P[4] , 则 P[0][1][2] === P[2][3][4] 则相当于 next[5] = next[4] + 1 ;

说明

2）如果P[i-1] != P[j] ， 则回溯 到 j = next[j] , 循环判断 P[j] 与 P[i-1] 的值。

 

 

实现代码： 

 

public class Kmp {
    public int[] GetNextArray(Stirng pattern) {
        int[] next = new int[pattern.length] ;
        for(int i=0, j=0; i< next.length; i++) {
            while(j!=0 && pattern.charAt(i-1) != pattern.charAt(j)){
                j= next[j] ;
            }
            if(pattern.charAt(i-1) == pattern.charAt(j)){
                j++;
            }
            next[i] = j;
        }
    }

    public int firstIndexOf(String s , String pattern) {
        int[] next = GetNextArray(pattern) ;
        for(int i=0, j=0 ;i<s.length();i++) {
            while(j!=0 && str.charAt(i) != pattern.charAt(j)){
                j = next[j] ;
            }
            if(s.charAt(i) == pattern.charAt(j)){
                j++;
            }
            if(j== pattern.length()){
                return i-j+1;
            }
        }
        return -1;
    }
}