剑指offer-树（JavaScript）

树

7. 重建二叉树

题目描述

输入某二叉树的前序遍历和中序遍历的结果，请重建该二叉树。假设输入的前序遍历和中序遍历的结果中都不含重复的数字。

例如，给出

前序遍历 preorder = [3,9,20,15,7]
中序遍历 inorder = [9,3,15,20,7]

返回如下的二叉树：

代码

/**
 * Definition for a binary tree node.
 * function TreeNode(val) {
 *     this.val = val;
 *     this.left = this.right = null;
 * }
 */
/**
 * @param {number[]} preorder
 * @param {number[]} inorder
 * @return {TreeNode}
 */
var buildTree = function(preorder, inorder) {
    if(preorder.length==0 || inorder.length==0) return null;
    var root=preorder[0];
    var index = inorder.indexOf(root);
    var left = inorder.slice(0, index);
    var right = inorder.slice(index+1);
    var node = new TreeNode(root);
    node.left = buildTree(preorder.slice(1,index+1), left);
    node.right = buildTree(preorder.slice(index+1), right);
    return node;
};

8. 二叉树的下一个节点

题目描述

给定一个二叉树其中的一个结点，请找出中序遍历顺序的下一个结点并且返回。注意，树中的结点不仅包含左右子结点，同时包含指向父结点的next指针。下图为一棵有9个节点的二叉树。树中从父节点指向子节点的指针用实线表示，从子节点指向父节点的用虚线表示。

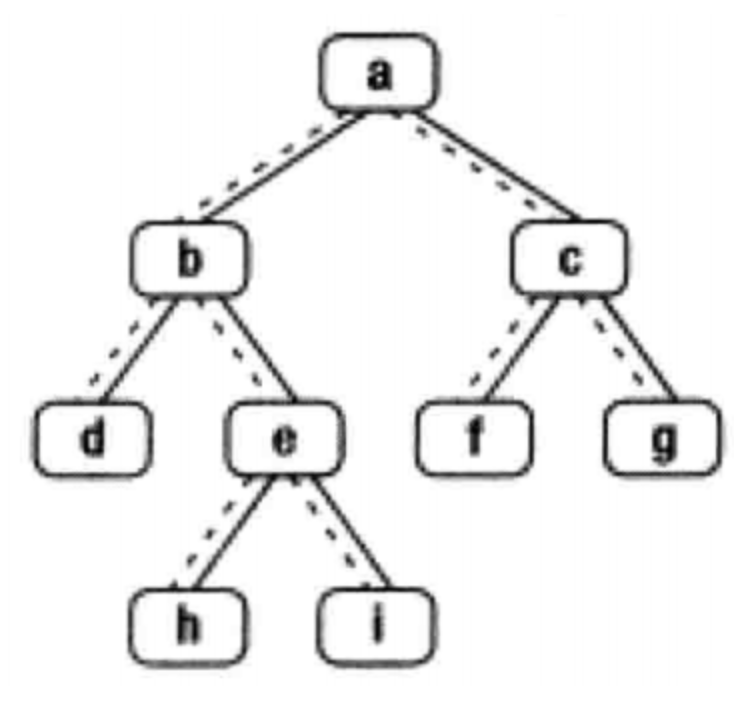
例如

输入:{8,6,10,5,7,9,11},8
返回:9
解析:这个组装传入的子树根节点，其实就是整颗树，中序遍历{5,6,7,8,9,10,11}，根节点8的下一个节点就是9，应该返回{9,10,11}，后台只打印子树的下一个节点，所以只会打印9，如下图，其实都有指向左右孩子的指针，还有指向父节点的指针，下图没有画出来

代码

/*function TreeLinkNode(x){
    this.val = x;
    this.left = null;
    this.right = null;
    this.next = null;
}*/

function GetNext(pNode) {
  // write code here
  if (pNode === null) return null; //空结点
  var p = null;
  if (pNode.right) {
    //有右子树，则下一个结点在右子树最左边的结点
    p = pNode.right;
    while (p.left !== null) {
      p = p.left;
    }
    return p;
  } else {
    //没有右子树
    p = pNode.next;
    if (p && p.right === pNode) {
      while (p.next && p.next.right === p) {
        p = p.next;
      }
      p = p.next;
    }
    return p;
  }
  return null;
}

26. 树的子结构

题目描述

输入两棵二叉树A和B，判断B是不是A的子结构。(约定空树不是任意一个树的子结构)
B是A的子结构，即 A中有出现和B相同的结构和节点值。

例如:
给定的树 A:

给定的树 B：

   4 
  /
 1

返回 true，因为 B 与 A 的一个子树拥有相同的结构和节点值。

示例 1：

输入：A = [1,2,3], B = [3,1]
输出：false

示例 2：

输入：A = [3,4,5,1,2], B = [4,1]
输出：true

代码

/**
 * Definition for a binary tree node.
 * function TreeNode(val) {
 *     this.val = val;
 *     this.left = this.right = null;
 * }
 */
/**
 * @param {TreeNode} A
 * @param {TreeNode} B
 * @return {boolean}
 */
var isSubStructure = function(A, B) {
    if(!A || !B) return false; 
    return isSame(A, B) || isSubStructure(A.left, B) || isSubStructure(A.right, B);
};
var isSame = function(A, B){
    if(!B) return true;
    if(!A) return false;
    if(A.val != B.val) return false;
    return isSame(A.left, B.left) && isSame(A.right, B.right);
}

27.二叉树的镜像

题目描述

请完成一个函数，输入一个二叉树，该函数输出它的镜像。

例如输入：

     4
   /   \
  2     7
 / \   / \
1   3 6   9

镜像输出：

	 4
   /   \
  7     2
 / \   / \
9   6 3   1

示例 1：

输入：root = [4,2,7,1,3,6,9]
输出：[4,7,2,9,6,3,1]

代码

/**
 * Definition for a binary tree node.
 * function TreeNode(val) {
 *     this.val = val;
 *     this.left = this.right = null;
 * }
 */
/**
 * @param {TreeNode} root
 * @return {TreeNode}
 */
var mirrorTree = function(root) {
    if(!root) return root;
    [root.left, root.right] = [root.right, root.left];
    mirrorTree(root.left);
    mirrorTree(root.right);
    return root
};

28.对称的二叉树

题目描述

请实现一个函数，用来判断一棵二叉树是不是对称的。如果一棵二叉树和它的镜像一样，那么它是对称的。

例如，二叉树 [1,2,2,3,4,4,3] 是对称的。

但是[1,2,2,null,3,null,3] 则不是镜像对称的:

示例 1：

输入：root = [1,2,2,3,4,4,3]
输出：true

示例 2：

输入：root = [1,2,2,null,3,null,3]
输出：false

代码

/**
 * Definition for a binary tree node.
 * function TreeNode(val) {
 *     this.val = val;
 *     this.left = this.right = null;
 * }
 */
/**
 * @param {TreeNode} root
 * @return {boolean}
 */
var isSymmetric = function(root) {
    if(!root) return true;
    return isSame(root.left, root.right)
};
var isSame = function(A, B){
    if(!A && !B) return true;
    if(!A) return false;
    if(!B) return false;
    if(A.val != B.val) return false;
    return isSame(A.left, B.right) && isSame(A.right, B.left); 
}

32-I.从上到下打印二叉树

从上到下打印出二叉树的每个节点，同一层的节点按照从左到右的顺序打印。

例如：

给定二叉树: [3,9,20,null,null,15,7],

[3,9,20,15,7]

代码

/**
 * Definition for a binary tree node.
 * function TreeNode(val) {
 *     this.val = val;
 *     this.left = this.right = null;
 * }
 */
/**
 * @param {TreeNode} root
 * @return {number[]}
 */
var levelOrder = function(root) {
    if(!root) return [];
    let nodes = [];
    nodes.push(root);
    let res = [];
    while(nodes.length > 0){
        node = nodes.shift();
        res.push(node.val);
        node.left && nodes.push(node.left);
        node.right && nodes.push(node.right);
    }
    return res;
};

32-II.从上到下打印二叉树II

题目描述

从上到下按层打印二叉树，同一层的节点按从左到右的顺序打印，每一层打印到一行。

例如:
给定二叉树: [3,9,20,null,null,15,7],

返回其层次遍历结果：

[
  [3],
  [9,20],
  [15,7]
]

代码

/**
 * Definition for a binary tree node.
 * function TreeNode(val) {
 *     this.val = val;
 *     this.left = this.right = null;
 * }
 */
/**
 * @param {TreeNode} root
 * @return {number[][]}
 */
var levelOrder = function(root) {
    if(!root) return []
    let nodes = [] // 存放当前节点
    let layer = 0 // 表示当前层数
    let res = []
    nodes.push(root)
    while(nodes.length){
        res[layer] = []
        let num = nodes.length
        while(num--){
            let node = nodes.shift()
            res[layer].push(node.val)
            node.left && nodes.push(node.left)
            node.right && nodes.push(node.right)
        }
        layer++
    }
    return res
};

33. 二叉搜索树的后序遍历序列

题目描述

输入一个整数数组，判断该数组是不是某二叉搜索树的后序遍历结果。如果是则返回 true，否则返回 false。假设输入的数组的任意两个数字都互不相同。

参考以下这颗二叉搜索树：

示例 1：

输入: [1,6,3,2,5]
输出: false

示例 2：

输入: [1,3,2,6,5]
输出: true

代码

/*
在二叉搜索树中：
1.若任意结点的左子树不空，则左子树上所有结点的值均不大于它的根结点的值。
2. 若任意结点的右子树不空，则右子树上所有结点的值均不小于它的根结点的值。
3.任意结点的左、右子树也分别为二叉搜索树。
*/
function VerifySquenceOfBST(sequence) {
  // write code here
  if (!sequence || !sequence.length) {
    return false;
  }
  return __VerifySquenceOfBST(sequence);
}

function __VerifySquenceOfBST(sequence) {
  const len = sequence.length;
  if (len < 2) return true;
  const root = sequence[len - 1];
  let i = 0;
  for (; i < len - 1 && sequence[i] < root; i++) {} //left的数量是i，0 -> i-1
  for (let j = i; j < len - 1; j++) {
    if (sequence[j] < root) {
      return false;
    }
  }
  return __VerifySquenceOfBST(sequence.slice(0, i)) && __VerifySquenceOfBST(sequence.slice(i, len - 1));
}

34. 二叉树中和为某一值的路径

题目描述

输入一棵二叉树和一个整数，打印出二叉树中节点值的和为输入整数的所有路径。从树的根节点开始往下一直到叶节点所经过的节点形成一条路径。

示例:
给定如下二叉树，以及目标和 target = 22，

          5
         / \
        4   8
       /   / \
      11  13  4
     /  \    / \
    7    2  5   1

[
   [5,4,11,2],
   [5,8,4,5]
]

代码

/* function TreeNode(x) {
    this.val = x;
    this.left = null;
    this.right = null;
} */

function FindPath(root, expectNumber) {
  // write code here
  var result = [];
  if (root === null) {
    return result;
  }
  dfsFind(root, expectNumber, [], 0, result);
  return result;
}

function dfsFind(root, expectNumber, path, sum, result) {
  sum += root.val;
  path.push(root.val);
  if (sum === expectNumber && root.left === null && root.right === null) {
    result.push(path.slice(0)); // 为什么不能直接push(path),因为在深度优先搜索的时候path都是指向的同一个
  }
  if (root.left !== null) {
    dfsFind(root.left, expectNumber, path, sum, result);
  }
  if (root.right !== null) {
    dfsFind(root.right, expectNumber, path, sum, result);
  }
  path.pop();
}

36. 二叉搜索树和双向链表

题目描述

输入一棵二叉搜索树，将该二叉搜索树转换成一个排序的循环双向链表。要求不能创建任何新的节点，只能调整树中节点指针的指向。

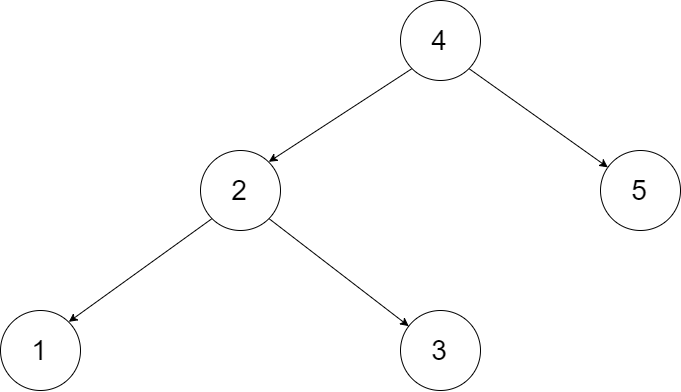
我们希望将这个二叉搜索树转化为双向循环链表。链表中的每个节点都有一个前驱和后继指针。对于双向循环链表，第一个节点的前驱是最后一个节点，最后一个节点的后继是第一个节点。

下图展示了上面的二叉搜索树转化成的链表。“head” 表示指向链表中有最小元素的节点。

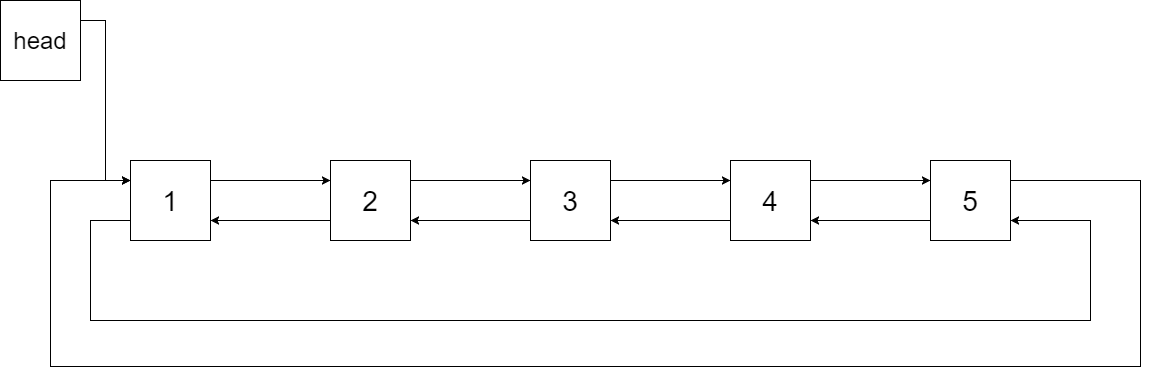
特别地，我们希望可以就地完成转换操作。当转化完成以后，树中节点的左指针需要指向前驱，树中节点的右指针需要指向后继。还需要返回链表中的第一个节点的指针。

代码

方法一：递归+数组

解题思路：

中序遍历一遍二叉搜索树，将节点保存在一个数组中。
遍历数组，更改每个节点的 left 和 right
返回数组第一个元素
时间复杂度是 O(N)，空间复杂度是 O(N)。相较于方法二，多开辟了 O(N)的数组空间。

/* function TreeNode(x) {
    this.val = x;
    this.left = null;
    this.right = null;
} */
function Convert(pRootOfTree) {
  // write code here
  if (!pRootOfTree) {
    return null;
  }
  const nodes = [];
  midTravel(pRootOfTree, nodes);
  const len = nodes.length;
  for (let i = 0; i < len; i++) {
    nodes[i].right = nodes[i + 1] || null;
    nodes[i].left = nodes[i - 1] || null;
  }
  return nodes[0];
}

//中序遍历,将所有节点存在nodes中
function midTravel(node, nodes) {
  if (node.left) {
    midTravel(node.left, nodes);
  }
  nodes.push(node);
  if (node.right) {
    midTravel(node.right, nodes);
  }
}

方法二：一次递归
二叉搜索树的性质是：左节点 < 当前节点 < 右节点。转换后的双向链表是有序的，这里采用中序递归遍历保证有序性。

设计的递归函数返回的是：已转换好的双向链表的尾结点，也就是当前节点的 left 指针应该指向的地方。递归函数的实现思路：

检查 left 是否为空，不为空，那么递归调用（传入左子树）
将 left 指针指向已转换好的双向链表的尾结点，并将尾节点的 right 指向当前节点
更新双向链表尾节点（变为当前节点），检查 right 是否为空，不为空，递归调用传入右子树）
返回转换后的双向链表尾节点
整个过程的要递归遍历一遍二叉树，时间复杂度是 O(N)，空间复杂度是 O(N)。

/* function TreeNode(x) {
    this.val = x;
    this.left = null;
    this.right = null;
} */

function Convert(pRootOfTree) {
  if (!pRootOfTree) {
    return null;
  }
  __Convert(pRootOfTree, null);
  let node = pRootOfTree;
  while (node.left) {
    node = node.left;
  }
  return node;
}

function __Convert(pRootOfTree, lastNodeInList = null) {
  if (!pRootOfTree) {
    return null;
  }
  // step1:左子树
  if (pRootOfTree.left) {
    lastNodeInList = __Convert(pRootOfTree.left, lastNodeInList);
  }
  // step2:当前节点
  pRootOfTree.left = lastNodeInList;
  if (lastNodeInList) {
    lastNodeInList.right = pRootOfTree;
  }
  // step3:右子树
  lastNodeInList = pRootOfTree;
  if (pRootOfTree.right) {
    lastNodeInList = __Convert(pRootOfTree.right, lastNodeInList);
  }

  return lastNodeInList;
}

37. 序列化二叉树

题目描述

请实现两个函数，分别用来序列化和反序列化二叉树

二叉树的序列化是指：把一棵二叉树按照某种遍历方式的结果以某种格式保存为字符串，从而使得内存中建立起来的二叉树可以持久保存。序列化可以基于先序、中序、后序、层序的二叉树遍历方式来进行修改，序列化的结果是一个字符串，序列化时通过某种符号表示空节点（#），以！表示一个结点值的结束（value!）。

二叉树的反序列化是指：根据某种遍历顺序得到的序列化字符串结果 str，重构二叉树。

代码

/* function TreeNode(x) {
    this.val = x;
    this.left = null;
    this.right = null;
} */

var arr = [];
function Serialize(pRoot) {
  // write code here
  if (!pRoot) {
    arr.push("#");
  } else {
    arr.push(pRoot.val);
    Serialize(pRoot.left);
    Serialize(pRoot.right);
  }
}
function Deserialize(s) {
  // write code here
  if (arr === null) return null;
  if (arr.length < 1) return null;
  var root = null;
  var temp = arr.shift();
  if (typeof temp === "number") {
    root = new TreeNode(temp);
    root.left = Deserialize(arr);
    root.right = Deserialize(arr);
  }
  return root;
}

54. 二叉搜索树的第k大节点

题目描述

给定一棵二叉搜索树，请找出其中第k大的节点。

示例 1:

输入: root = [3,1,4,null,2], k = 1
   3
  / \
 1   4
  \
   2
输出: 4

示例 2:

输入: root = [5,3,6,2,4,null,null,1], k = 3
       5
      / \
     3   6
    / \
   2   4
  /
 1
输出: 4

代码

/**
 * Definition for a binary tree node.
 * function TreeNode(val) {
 *     this.val = val;
 *     this.left = this.right = null;
 * }
 */
/**
 * @param {TreeNode} root
 * @param {number} k
 * @return {number}
 */
var kthLargest = function(root, k) {
    let res
    let num = 0
    const dfs = function(root){
        if(root === null){
            return 
        }
        dfs(root.right)
        num++
        if(num === k){
            res = root.val
        }
        dfs(root.left)
    }
    dfs(root)
    return res
};

55-I. 二叉树的深度

题目描述

输入一棵二叉树的根节点，求该树的深度。从根节点到叶节点依次经过的节点（含根、叶节点）形成树的一条路径，最长路径的长度为树的深度。

例如：

给定二叉树 [3,9,20,null,null,15,7]，

返回它的最大深度 3 。

代码

/**
 * Definition for a binary tree node.
 * function TreeNode(val) {
 *     this.val = val;
 *     this.left = this.right = null;
 * }
 */
/**
 * @param {TreeNode} root
 * @return {number}
 */
var maxDepth = function(root) {
    if(root === null) return 0
    return Math.max(maxDepth(root.left), maxDepth(root.right))+1
};

55-II. 平衡二叉树

题目描述

输入一棵二叉树的根节点，判断该树是不是平衡二叉树。如果某二叉树中任意节点的左右子树的深度相差不超过1，那么它就是一棵平衡二叉树。

示例 1:

给定二叉树 [3,9,20,null,null,15,7]

返回 true 。

代码

function IsBalanced_Solution(pRoot) {
  return depth(pRoot) !== -1;
}

// 用递归来判断root是不是平衡二叉树，如果不是则返回最大的深度，如果不是则返回-1
function depth(root) {
  if (root === null) return 0;
  var left = depth(root.left);
  if (left === -1) return -1;
  var right = depth(root.right);
  if (right === -1) return -1;
  if (Math.abs(left - right) > 1) {
    return -1;
  } else {
    return 1 + Math.max(left, right);
  }
}

68-I. 二叉搜索树的最近公共祖先

题目描述

给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。

百度百科中最近公共祖先的定义为：“对于有根树 T 的两个结点 p、q，最近公共祖先表示为一个结点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”

例如，给定如下二叉搜索树: root = [6,2,8,0,4,7,9,null,null,3,5]

示例 :

输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8
输出: 6 
解释: 节点 2 和节点 8 的最近公共祖先是 6。

输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 4
输出: 2
解释: 节点 2 和节点 4 的最近公共祖先是 2, 因为根据定义最近公共祖先节点可以为节点本身。

代码

/**
 * Definition for a binary tree node.
 * function TreeNode(val) {
 *     this.val = val;
 *     this.left = this.right = null;
 * }
 */
/**
 * @param {TreeNode} root
 * @param {TreeNode} p
 * @param {TreeNode} q
 * @return {TreeNode}
 */
var lowestCommonAncestor = function(root, p, q) {
    while(root){
        if(root.val<p.val && root.val<q.val){
            root = root.right
        } else if(root.val>p.val && root.val>q.val) {
            root = root.left
        } else {
            break
        }
    }
    return root
};

68-II. 二叉树的最近公共祖先

题目描述

例如，给定如下二叉树: root = [3,5,1,6,2,0,8,null,null,7,4]

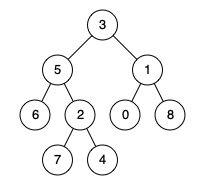
示例 1:

输出: 3
解释: 节点 5 和节点 1 的最近公共祖先是节点 3。```

示例 2:

输出: 5
解释: 节点 5 和节点 4 的最近公共祖先是节点 5。因为根据定义最近公共祖先节点可以为节点本身。```

代码

/**
 * Definition for a binary tree node.
 * function TreeNode(val) {
 *     this.val = val;
 *     this.left = this.right = null;
 * }
 */
/**
 * @param {TreeNode} root
 * @param {TreeNode} p
 * @param {TreeNode} q
 * @return {TreeNode}
 */
var lowestCommonAncestor = function(root, p, q) {
    if (!root || root === p || root === q) return root;
    const left = lowestCommonAncestor(root.left, p, q);
    const right = lowestCommonAncestor(root.right, p, q);
    // 左子树找不到，返回右子树
    if (!left) return right;
    // 右子树找不到，返回左子树
    if (!right) return left;
    // 左右子树都找到了，那么root就是要找的
    return root;
};

posted @ 2021-07-02 20:11 zerozhupan 阅读(48) 评论(0) 收藏举报

刷新页面返回顶部

登录后才能查看或发表评论，立即登录或者逛逛博客园首页

树

7. 重建二叉树

题目描述

代码

8. 二叉树的下一个节点

题目描述

代码

26. 树的子结构

题目描述

代码

27.二叉树的镜像

题目描述

代码

28.对称的二叉树

题目描述

代码

32-I.从上到下打印二叉树

代码

32-II.从上到下打印二叉树II

题目描述

代码

33. 二叉搜索树的后序遍历序列

题目描述

代码

34. 二叉树中和为某一值的路径

题目描述

代码

36. 二叉搜索树和双向链表

题目描述

代码

37. 序列化二叉树

题目描述

代码

54. 二叉搜索树的第k大节点

题目描述

代码

55-I. 二叉树的深度

题目描述

代码

55-II. 平衡二叉树

题目描述

代码

68-I. 二叉搜索树的最近公共祖先

题目描述

代码

68-II. 二叉树的最近公共祖先

题目描述

代码

公告

搜索

常用链接

随笔档案

相册